混凝土随机损伤本构理论验证

为了验证弹塑性随机损伤本构关系的正确性，本书进行了比较系统的试验研究，具有翔实的实验数据，能够同时在均值和方差两个层次验证本书模型。

首先简要介绍用于模型验证的静力试验结果。2006年，本书采用INSTRON8506四立柱液压伺服试验机对混凝土一维、二维本构关系进行了系统的试验研究。在应变控制加载的条件下测得了混凝土板式试件单轴受拉、单轴受压以及二轴压-压和拉-压的双轴应力-应变全曲线，试验的详细细节信息如下：

（1）试件制备

试件材料为高性能混凝土，设计强度等级为C50。混凝土制备采用了双掺工艺，胶凝材料中除水泥外还掺有一定量的粉煤灰和矿渣粉，骨料采用粒径5—15mm碎石。每立方米高性能混凝土的配合比（重量比）为：水∶水泥∶矿粉∶粉煤灰∶砂∶石∶减水剂=175∶204∶204∶102∶175∶640∶1 100∶15.5（kg）。制备过程中先将试件浇筑成520mm×520mm×50mm的方板，采用木模成型，人工浇注，机械振捣，24h拆模，标准养护28d。然后采用红外线自动桥式切割机将养护好的方板切割成150mm×150mm×50mm的小试件进行试验。切割所得小试件表面光滑平整，易于同加载钢板接合，并且试件几何尺寸也具有很高的精度。

（2）试验设备

加载设备采用清华大学高坝大型实验室INSTRON8506四立柱液压伺服试验机。双向加载系统为分离式，竖向为四立柱试验机，水平为封闭加力框架，两个方向可以互不干扰地实现力的输出。在水平和竖直方向上分别安装高精度应变测量装置（这里采用引伸仪）并将测得的应变实时传回试验机，即构成以应变为控制参数的闭环控制（closed loop）加载系统，实现各自方向上的应变输出。此时根据设计应变比和加载速率计算出各个时刻的控制应变，再以加载控制文件的形式输入试验机，即可以实现应变比例加载。图3-5给出了双轴加载试验的试件布置。

图3-5　双轴加载示意图

（3）加载制度

在应力控制加载制度下加载到达峰值点后就会进入非稳定阶段，试件将瞬间发生破坏，此时不能测得应力-应变曲线的下降段，而在应变控制加载制度下试件在加载全过程都处于稳定状态，可以测得应力-应变全曲线，所以本次试验采用应变控制加载制度。在双轴加载过程中，保持名义应变比不变，并且根据应变比的不同将所有试件分为8组。压-压区4组，应变比分别为1、0.3、0.1和0；拉-压区4组，应变比分别为-0.167、-0.25、-0.5和-∞；由于试验条件的限制，没有进行双向受拉区的试验。

下面进行理论与实验结果的对比。对比的过程遵循这样的原则：对于单轴加载全曲线，采用试验实测结果拟合得到单轴损伤演化的参数（λ±，ζ±，ξ±）；然后采用单轴试验结果识别得到的参数，代入前述本构关系，对二维试验结果进行预测，进而与实测二维全曲线进行对比，以验证模型的正确性和有效性。

（1）单轴受拉应力-应变关系

首先考虑单轴受拉情况。根据试验结果，按照随机建模规则，识别得到单轴受拉模型参数为E0=37 559MPa，λ+=4.92，ζ+=0.30，ξ+=40，=0.70。试验结果与模型结果的对比如图3-6。

图3-6　单轴受拉结果(www.xing528.com)

（2）单轴受压应力-应变关系

对于单轴受压，根据试验结果，按照随机建模规则，识别得到单轴受压模型参数为E0=37 559MPa，λ-=7.77，ζ-=0.37，ξ-=50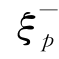，=0.20。试验结果与模型结果的对比如图3-7。

图3-7　单轴受压结果

值得指出的是，虽然采用了同一批试验数据，但是由于本书工作与本课题组之前的工作［52］在塑性变形建模中采用了不同的处理方式，故本书的模型参数识别工作是独立进行的。

（3）双轴受力全曲线

采用单轴全曲线试验拟合得到的参数，对二维加载（σ3=0）结果进行了数值模拟，双轴等压加载条件下的数值与试验结果对比如图3-8。可见，试验结果在均值和方差意义上均与试验结果有一定的一致性，这从一个侧面说明了模型的有效性。

（4）双轴强度包络线

双轴强度包络线的结果及与试验结果的对比如图3-9。除了本课题组的试验结果，图中还包括了若干经典试验结果［98，138，139］。从图中可以看出，大部分试验结果都落在了均值±标准差的区域中。可见：本书采用的模型不仅能够预测双轴应力作用下混凝土强度的提高和降低，还能给出强度波动的范围。

图3-8　双轴受压结果ε2／ε1=-1／-1

图3-9　双轴强度包络图