多尺度混凝土随机损伤本构理论研究成果

为明晰计，以单轴受拉为背景展开论述。此时，可将一维受力试件简化成串并联弹簧系统［48］（图3-1）。所有弹簧并联在一系列刚性板之间。此时材料的细观性能用细观弹簧的性能表示，而材料的宏观性能用串并联弹簧系统表示。

图3-1　细观弹簧模型

图3-2　理想弹性-断裂应力-应变关系

为了描述混凝土细观断裂过程，可以假设细观弹簧具有如图3-2所示理想弹性-断裂性能。与Kandarpa模型［47］不同，细观随机断裂模型中基本变量是断裂应变。显然，从混凝土损伤的物理背景考察，每一根细观弹簧的断裂应变是不同的，为随机变量。在外力作用下，整个微弹簧系统就会经历由细观弹簧的断裂而引发的应力重分布过程。这一过程，既可以发生在不同的串联单元之间，也可以发生在同一并联弹簧组内部。为简明计，可以用如图3-3所示的顺次断裂过程说明因断裂导致的应力重分布进而导致系统平均应力的跌落的过程。由于每个弹簧在未断裂之前均保持线弹性性质，在下一次弹簧断裂之前，整个系统的平均应力保持线性增长，仅由于前面弹簧的断裂导致了系统平均弹性模量的减小。对于离散并联单元组，应力的线性增长与跌落的交替作用将形成如图3-3所示的锯齿曲线。

考虑基于面积的损伤定义，有

图3-3　离散并联单元模型的平均应力-应变曲线

此处Ad为断裂部分的面积，而A为总面积。

对于串并联弹簧系统，如果假定每一根弹簧具有相同的面积，根据上述损伤定义，可得其损伤变量为

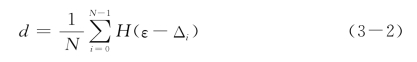
此处N为弹簧的总数，Δi为第i根弹簧的断裂应变，而H（·）为Heaviside函数。

随着细观弹簧数目的增加，即N→∞，考虑随机积分的定义，可得

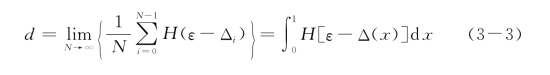
其中，Δ（x）为一维断裂应变随机场；x表示细观单元的空间坐标。

显然，当N→∞时，每一根细观弹簧造成的系统应力跌落将趋于一个小量，由此，系统的平均应力-应变曲线就由锯齿曲线变成光滑曲线，如图3-4。式（3-3）就是基于串并联模型得到的宏观损伤演化方程。这一方程包含随机场Δ（x）和Heaviside函数，因此还需要进一步考察。

首先考虑对随机断裂随机场的描述。假定材料的细观断裂随机场为平稳随机场，则其一阶密度函数与空间坐标无关，可以表示为

图3-4　连续并联单元模型的平均应力-应变曲线

而二阶相关密度函数只与两点之间的相对距离有关，表示为

考虑由平稳随机场Δ（x）生成的随机场

显然θ（x）为（0，1）随机场，其分布函数为

此处P｛·｝表示事件发生的概率；F（·）定义为随机变量的分布函数，为随机变量密度函数的积分。

随机场θ（x）的集合平均

其中E（·）为期望算符，表示随机变量的集合平均。

利用式（3-9），可得随机损伤演化式（3-3）的均值函数，即

(www.xing528.com)

为求解随机损伤的二阶特征量。考虑二维生成随机场

显然ϑ（x1，x2）亦为（0，1）随机场，其分布函数

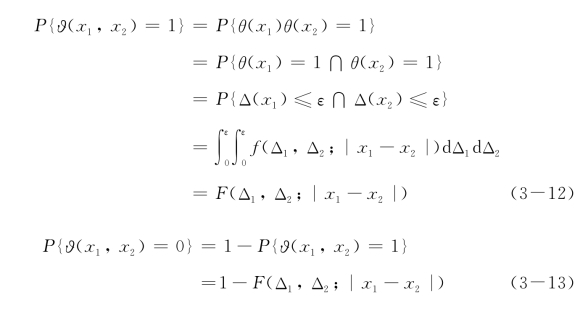
其中F（Δ1，Δ2；｜x1-x2｜）定义为随机场Δ（x）的二维相关分布函数。

损伤变量的方差

根据随机场均方积分的性质［135］，有

将均方积分式（3-15）代入式（3-14），可解得损伤的方差表达式为

如果Δ（x）为独立同分布序列，那么有

代入式（3-16），可得损伤的方差演化

上式说明，若完全忽略随机场的相关性，随机损伤将退化为确定性损伤。

下面考虑细观随机场的具体表达式。在混凝土强度的统计中，一般将混凝土的强度参数的分布取为对数正态分布；而Bazant and Becq-Giraudon［136］的研究中，也将混凝土的断裂强度取为对数正态分布。因此在细观弹簧服从理想弹性-断裂应力-应变关系条件下，取断裂-应变场为对数正态随机场是合理的。为此，取

为平稳正态随机场，其均值和方差为（λ，ζ2）。令（μΔ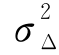，）表示Δ（x）的均值和方差，则两组均值与方差的换算关系为

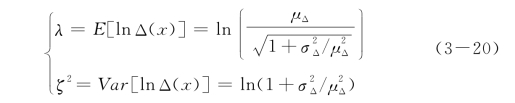
定义对数正态分布与标准正态分布的变换关系如下

则对数正态随机场的一维与二维分布函数可以用标准正态分布的一维与二维分布函数表示如下

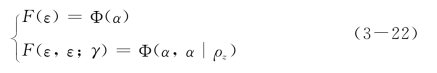
其中，ρz（γ）为相关函数，一般可取为指数函数形式，即

这里ξ为材料的相关长度。

式（3-22）中，Φ（α）和Φ（α，α｜ρz）分别为标准正态分布的一维、二维分布函数。在数值计算中，前者一般采用有理函数逼近，后者则一般采用下述公式转化成一维数值积分［137］，即

积分上限

上述细观力学模型引入了3个参数（λ，ζ，ξ）表示随机损伤的演化过程。由于混凝土在单轴受拉和受压作用下强度和变形的差别明显，所以需要求用两组不同的参数，即（λ+，ζ+，ξ+）和（λ-，ζ-，ξ-），分别反映受拉与受压的随机损伤的演化。