基于多尺度分析的动力非线性分析成果

1999年，Kulkarni和Shah［134］对钢筋混凝土梁进行了静力与动力加载试验研究，得到了一系列的实验结果。试验用钢筋混凝土梁的几何形状、配筋状况以及加载装置见图2-21，其加载程序如表2-1所示。所有的混凝土梁截面均采用图2-21所示的统一截面，且没有配置腹筋用于抗剪。

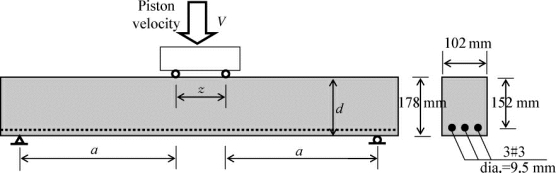
图2-21　试验构件和加载装置

表2-1　梁试件的加载程序

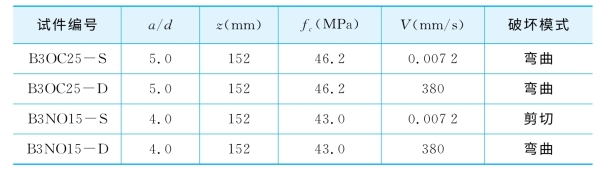
本书选择了上述实验中的四根梁的实验结果，采用平面有限元模型结合本书所发展理论进行了数值模拟。数值分析中混凝土单元类型为平面四节点单元，钢筋作为rebar layers直接设置到对应的混凝土单元中。数值模拟中所采用的混凝土的弹性模量E0=37 000MPa，泊松比ν0=0.2，密度ρ0=2 400kg／m3，其他与损伤演化有关的参数见表2-2。钢筋采用线性硬化弹塑性模型，不考虑材料的率敏感性，计算中材料参数取为：弹性模量Es=210GPa，屈服强度fy=580MPa，塑性硬化模量Ep=0.01Es。

表2-2　混凝土计算参数

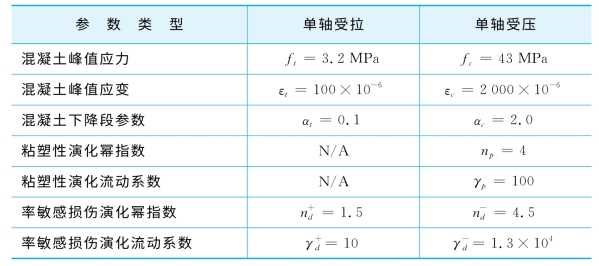
数值模拟结果与实验结果对比如图2-22和图2-23。分析可见，B3OC25型试件的结果（图2-22）体现了材料动态强度的提高对于结构性能的直接影响。随着材料在动力荷载作用下强度提高，构件的强度和延性都有所提高，构件的破坏模式没有改变。本书采用的模型与实验结果符合较好。(www.xing528.com)

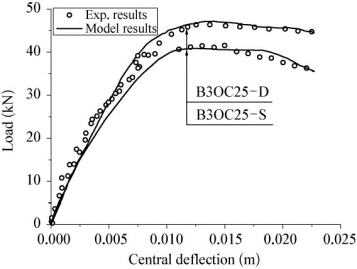
图2-22　B3OC25型试件荷载位移曲线

图2-23　B3NO15型试件荷载位移曲线

B3NO15型试件的结果（图2-23）体现了率效应对构件破坏形态的本质性影响。由于高应变率作用下材料强度提高的幅度不一致，导致试件在拟静力与动力作用下表现出完全不同的破坏模式。试件B3NO15-S为剪切破坏，而B3NO15-D为弯曲破坏。本书采用的模型很好地反映了这一特点，模型预测结果与实验结果具有定量的一致性。

动态强度提高引起破坏模式转换可根据图2-24进行分析。图2-24给出了固定截面和配筋条件下梁的极限破坏荷载与混凝土强度的关系曲线，其中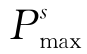表示受剪破坏极限荷载与混凝土抗压强度fc的关系曲线，而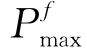表示受弯破坏极限荷载与混凝土抗压强度fc的关系曲线，它们把破坏区分为三个区域（中间部分形成所谓“剪切破坏谷”），动力荷载引起的强度提高将有可能引起梁的破坏模式的转变。本书例子位于图2-24右侧的转换点，动力作用下由受剪破坏转换为受弯破坏；如果配筋充足而接近图2-24左侧的转换点，那么就有可能在动力作用下受弯破坏转换为受剪破坏。这从一个侧面说明，仅仅将动力强度提高作为混凝土构件或者结构的储备强度，在特定情况下（譬如说高配筋率情况）可能是偏于不安全的。

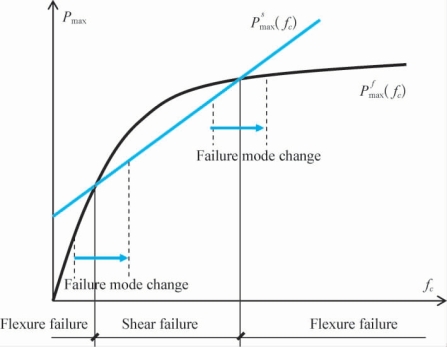
图2-24　强度提高引起的破坏模式转换