多尺度分析揭示混凝土本构关系

由于需要考虑材料的多维损伤和塑性，上述弹塑性损伤本构关系具有一定的复杂性，若要应用于实际结构的非线性分析，需要借助于适当的数值算法。20世纪80年代以来，研究者对非线性本构关系的数值算法进行了系统的研究［23，28，30，130-132］，建立了一类高效的数值算法，称为回映算法（return-mapping algorithm）。本节将对弹塑性损伤本构关系的回映算法进行简要的讨论。

首先考虑弹塑性损伤本构关系（2-11）的率形式，有

由于前面的建模过程中考虑了有效应力空间塑性力学，所以式（2-127b）是闭合的，可以先单独求解，得到塑性应变及有效应力；然后再求解损伤演化，最后根据式（2-127a）得到应力。

上述求解过程构成了算子分解（operator split）方法［28，132］的基本过程，详述如下：

（1）弹性预测

首先根据整体结构的分析，给定应变率

弹性预测步中，先冻结塑性演化与损伤演化，即

由于认为材料只有弹性变形，可得有效应力率

和柯西应力率

（2）塑性修正

如果材料发生塑性变形，则需要根据塑性应变演化方程修正弹性预测步中所得的结果。在塑性修正步中总应变率取为0，即

将塑性、黏塑性应变演化统一标识为如下形式

对于塑性演化，屈服函数F取

而对于黏塑性演化，屈服函数F取

有效应力率

前已述及，本书采用的塑性理论直接建立在有效应力空间，所以塑性修正步冻结损伤演化，有

最后得柯西应力率

（3）损伤修正

当材料发生损伤时，需要根据损伤值修正弹塑性预测结果，在损伤修正步中，仍然取

冻结塑性变形演化，有(www.xing528.com)

进而有有效应力率

考虑双标量损伤模型，有柯西应力变化率

根据Faria et al［30］以及Wu et al［39］的讨论，有效应力正、负分量的变化率可表示为

正、负投影率张量

考虑率相关损伤演化之后，损伤变化率为

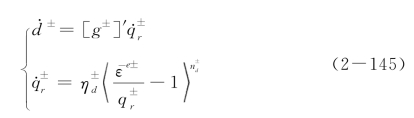
算子分解体系将弹塑性损伤本构关系的微分方程分解到三个相对独立的子空间独立求解，大大简化了求解过程。上述三个步骤中，弹性预测步骤只需要处理线性系统，相对简单；后两个步骤中则都需要处理一阶非线性微分系统，需要进一步说明。

一般形式的一阶非线性微分系统可以表示为

一阶微分系统的数值求解方法有两类，即显式方法和隐式方法。

显式方法中最基本的是前进Euler方法，将微分系统离散为差分系统，有

此处，Δtn+1=tn+1-tn。

基于上式，可以利用第n步的数值结果直接求第n+1步的数值结果。显式方法的整个求解过程不需要迭代，计算简便，但是需要非常小的时间步长Δtn+1才能保证计算的精度，所以适用于冲击碰撞等瞬时问题。为了提高计算精度，减少时间离散步的步数，可以考虑龙格-库塔法等高阶算法。但在处理强非线性系统的过程中，高阶方法容易出现稳定性问题。

完全隐式方法主要是后退Euler算法，此时所建立数值差分系统为

由于求解中还需要用到第n+1步的函数值，也就是待求函数值Sn+1，对于一般非线性问题上式就不能直接显式解出，需要进一步迭代求解。在每一个加载步考虑非线性系统

采用牛顿迭代法求解非线性方程的基本公式

将非线性系统式（2-149）代入离散系统式（2-150），整理可得

迭代直至，即可得第n+1步的数值解。

隐式分析方法虽然每一步均需要迭代，但是如果系统的雅可比矩阵∂Ξ／∂S稳定性较好，使得整个数值系统稳定的时间步长Δtn+1较大，总体上就可以减少时间过程数值离散的步数。所以，隐式方法适用于静力非线性问题或者时间过程比较长的问题。理论上讲，其时间积分具有无条件稳定性。

将算子分解体系与隐式求解方法结合，可以得到弹塑性损伤本构关系的基本求解过程：首先进行弹性预测，得到最大的可能有效应力增量和柯西应力增量；然后进行塑性修正，利用牛顿迭代方法求得塑性应变，并将有效应力“回映”到屈服面上（图2-12）；最后进行损伤修正，利用牛顿迭代法求出损伤变量，最后“回映”修正柯西应力。由于上述过程中，弹性预测与非线性修正是“试探”与“回映”的关系，所以基于上述思路建立起来的本构关系数值算法称为回映算法（return-mapping algorithm）［132］。回映算法在每一个加载步都保证迭代收敛并严格满足屈服条件，所以算法精度较高。同时，由于其基础算法即后退欧拉算法是无条件稳定的，使回映算法的算法稳定性也很好，非常适合于本构关系的数值求解。

图2-12　回映算法示意图