动力强度提高因子一般定义为混凝土动力强度与静力强度的比值，是衡量混凝土率效应的重要指标。由于其非常便于试验测量和记录，所以经过几十年的研究，已经积累起了大量的实验数据。
现行的混凝土动力提高因子的模型一般取为应变率的指数函数或者对数函数［110，119］，也有学者将实验数据分段用指数或对数函数拟合，形成分段函数模型。本节基于双标量弹塑性损伤模型及其率相关推广，在若干简化假定的基础上，推导得到混凝土动力强度提高因子的解析表达式。
首先将多维弹塑性损伤本构关系简化到一维，可得
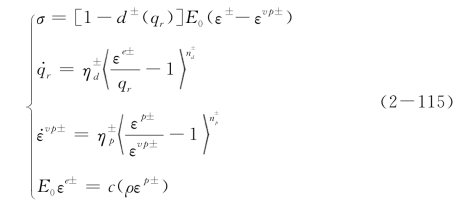
上述一维本构关系同时考虑了损伤演化与塑性变形演化及其对应的率敏感性，表达式偏于复杂，不利于解析分析。为了解得动力提高因子，这里先略去塑性应变，只考虑损伤引起的非线性的影响，有
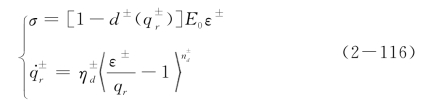
本节最后的数值结果表明，塑性应变对于动力提高因子的影响不大。
考虑匀速加载情况，应变函数可以表示为
代入单轴动力本构关系式（2-116），整理可得
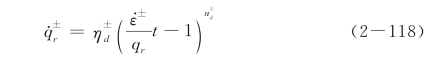
式（2-118）为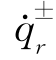
的一阶常微分方程，自变量为t。不失一般性，可假定其初始条件为
考虑微分方程的试探解形式为
其中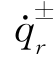
为动力能量等效应变的变化率，取为常数。
将试探解式（2-120）代入方程式（2-118），可得
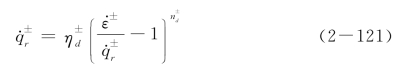
由于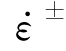
与
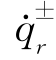均为常数，上式为
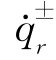的代数方程。可以看出，由方程式（2-121）解出动力损伤驱动力变化率
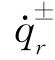，可以使得试探解式（2-120）同时满足原微分方程式（2-118）与初始条件式（2-119）。将式（2-121）整理，可得(www.xing528.com)
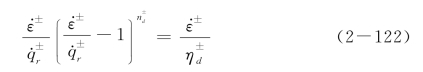
考虑式（2-117）与式（2-120），可得单轴应变与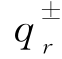
的换算关系
将上述换算关系代入单轴动力本构关系式（2-116），整理可得
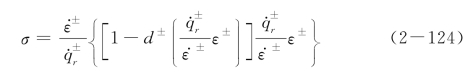
上式大括号内部分的极值为混凝土的静力强度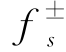
，因此对上式求极值可得动力强度为
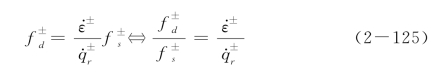
将式（2-125）代入式（2-122），可得动力强度提高因子的代数方程
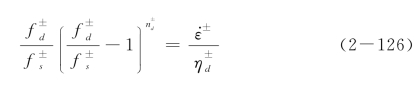
据此可以解出动力强度提高因子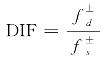
随加载应变率
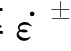的变化曲线。对于单轴受拉和单轴受压，率相关性是不同的，所以与率敏感性相关的材料参数
也需要取不同的数值。
单轴受压动力提高因子计算结果与试验结果［101-115］的对比如图2-10所示。图中也给出了同时考虑塑性变形的弹塑性损伤模型结果（材料参数：
）与忽略塑性变形的弹性损伤模型结果（材料参数：
）。弹塑性损伤模型的结果是基于数值方法计算得到，而弹性损伤模型结果直接基于动力提高因子解析解（2-126）。由图中可以看出：弹塑性损伤模型结果与弹性损伤模型结果基本重合，也说明塑性应变对材料动力强度提高的影响不大。
单轴受拉动力提高因子计算结果与试验结果［103，106，116-121］的对比如图2-11所示。计算中材料参数取：
。可以看出：本书建立的动力强度提高因子的解析模型能够很好地反映混凝土的动力强度提高。
本书模型的表达简单，所需材料参数少，非常适合于实际工程的分析设计。
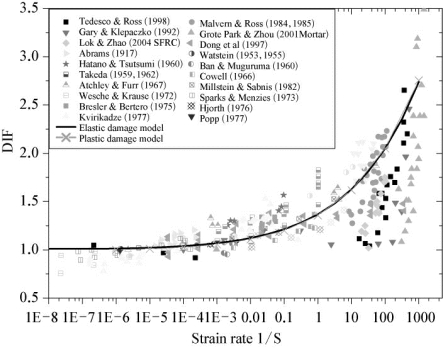
图2-10 单轴受压动力强度提高因子
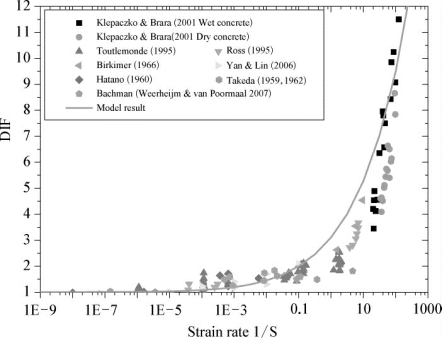
图2-11 单轴受拉动力强度提高因子
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
