混凝土随机损伤本构理论多尺度分析

为了考虑混凝土的率相关性，需考虑混凝土静力本构关系的动力拓展。对于塑性子空间部分，其对应的率相关拓展大多基于黏塑性力学［128，129］。黏塑性力学的基本思路可采用图2-9表示。图2-9中应力到达屈服点之后，滑动元件开始发生滑移，产生塑性变形，同时黏性元件也开始承受外力，滑动元件与黏性元件的共同作用，使得总应力可以超过屈服点，产生“过应力”。此时若维持外部变形不变，那么黏性原件承受的应力将逐渐释放，应力逐渐返回到屈服点，“过应力”消失。常用的黏塑性理论模型有两大类：对于线性黏塑性应变演化，一般采用Duvaut-Lions模型［129］；对于非线性黏塑性演化，一般采用Perzyna模型［128］。本节基于后者对有效应力空间塑性理论进行了黏塑性拓展，建立了有效应力空间黏塑性理论。

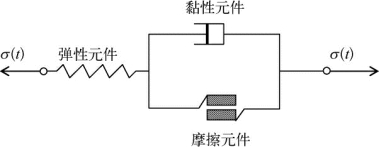
图2-9　黏塑性理论示意

首先考虑有效应力表达式的率形式

式中用黏塑性应变εvp代替了塑性应变εp，表明此处考虑了率相关演化。

黏塑性应变的演化与塑性应变的演化具有类似的形式，表达式为

根据前面的讨论，考虑黏塑性演化之后，应力可以高于屈服应力，这意味着塑性一致性条件（2-68）不再满足。因此不能再用一致性条件解得黏塑性流动因子λvp。一般地，类比Perzyna模型［128］，可给出黏塑性流动因子表达式

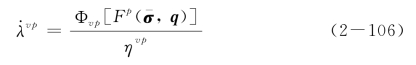
其中，Φvp（·）为黏塑性流动函数。

反解式（2-106），可得黏塑性屈服函数

其中

为率敏感材料的过应力函数。利用黏塑性材料的屈服条件（2-107），可得黏塑性理论的Kuhn-Tucker条件为(www.xing528.com)

Perzyna［128］建议了黏塑性流动函数的几种形式

本书基于最常用的幂函数形式定义粘塑性流动函数，即取

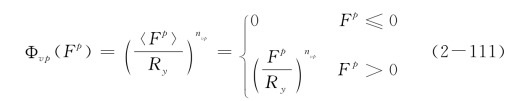
其中，Ry为屈服函数的半径。

此时，过应力函数

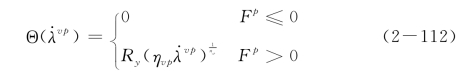
对于经验塑性模型，亦可引入黏塑性修正如下：

其中塑性等效塑性应变可由式（2-87）求出，等效黏塑性应变由下面微分方程解出

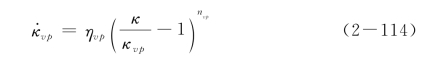
其中，ηvp与nvp为黏塑性力学引入的两个与材料率敏感性相关的材料参数。

如果加载速率非常慢，即，由上式可解得黏塑性应变等于塑性应变。