混凝土随机损伤本构理论及多尺度分析

在外力的作用下，结构不可避免的要进入非线性。特别是对土木结构的分析设计，简单地忽略非线性段而只考虑材料的线性性能会导致投资的浪费。然而另一方面，材料的非线性表现又是非常复杂的，对于不同的材料而言，其非线性具有本质的区别，很难加以统一地考虑。所以对于材料非线性的考虑必须根据材料的特性加以针对性的考虑。前已述及，对于混凝土等脆性材料而言，其非线性产生的本质是内部微裂缝的产生和发展导致的“软化”和“弱化”，因此，混凝土的非线性性能特别适合用损伤力学理论加以反映。这里，将围绕损伤理论来讨论均匀化方法的非线性推广及相应的多尺度损伤理论。

1999年以来，Fish及其合作者推广了经典摄动均匀化方法，建立了一类多尺度损伤理论［84，85］，考虑了损伤在多个尺度上的演化。在这一理论中，宏观尺度上材料的“软化”和“弱化”采用宏观损伤变量考虑，而微观尺度上材料中微裂缝的产生和扩展用微观损伤考虑。为了建立统一的均匀化方法体系，除了位移场的摄动展开式（1-52），另外引入损伤变量的摄动展开如下

这里ω表示损伤标量。

考虑微观损伤引起的非线性，有应力-应变关系

将应变摄动展开式（1-53）和损伤摄动展开式（1-61）代入上面应力-应变关系，整理可得应力展开式

其中各阶应力摄动项

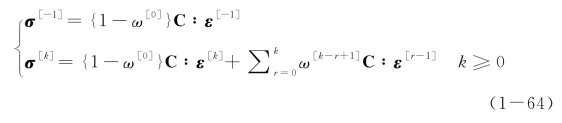
代入平衡方程，经过一系列数学处理［84］，可得微观损伤引起的附加应变与宏观应变之间有如下简单的换算关系

其中应变转换系数

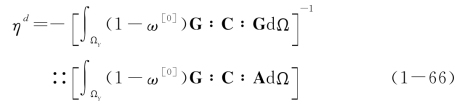
其中张量A为无损材料宏观和微观应变的转换张量，可以由无损材料的特征张量表示为

无损材料的特征函数χ（y）可以由对应无损材料的特征方程（1-57）解出。张量G与A的关系为

(www.xing528.com)

其中I为4阶对称单位张量，其表达式为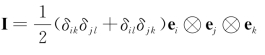

Fish多尺度损伤模型试图从多个尺度描述复合材料损伤的产生和发展过程，在经典均匀化理论中引入损伤标量的多尺度展开，用以描述各个尺度损伤之间的联系，最终建立一个比较完整的多尺度损伤理论体系。而Fish模型的局限性也相当明显，多尺度损伤的摄动展开更多是为了便于数学上的处理，但是这种描述方式却在某种程度上掩盖了损伤的物理机制。这种从一个尺度的抽象损伤再到另一个尺度上的抽象损伤的建模过程并没有深化人们对损伤的认识。虽然可以由细观尺度的损伤演化计算得到宏观尺度的损伤演化，但是细观尺度的损伤演化还是要依赖于直接的实验测定，其实验测定的难度并不低于宏观损伤演化。所以这一类模型从本质上看并没有完整地体现出多尺度思想的实质。

细观尺度的损伤表现为具象的微裂缝和微缺陷的发展。近年来，Dascalu及其合作者［86-88］以及Alfaro et al［89］研究者初步探索了由细观尺度微裂缝演化得到宏观尺度损伤演化的多尺度理论框架，有迹象表明，这一方向上的研究正在成为固体力学的热点内容。

根据Dascalu et al［86，87］的理论，首先将微裂缝看作微观结构的一部分，并对包含微裂缝的材料结构（图1-7）直接进行均匀化，可得其均匀化应变、应力以及特征张量等表达式，这些结果与经典均匀化方法的结果一致。

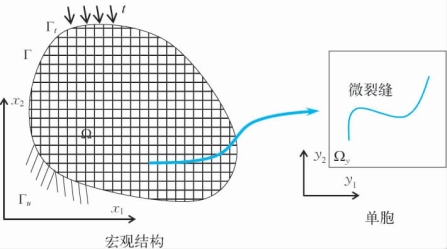
图1-7　包含微观裂纹的材料多尺度结构

Dascalu et al［86］将损伤定义为微裂缝长度与微观单元体长度的比值，如果微观单元体取单位长度，那么损伤就直接等于微观裂缝的长度。那么在能量分析的基础上，可得如下能量平衡方程

式（1-69）左边第一项为单元体弹性能变化率，第二项为裂缝扩展能量耗散率，右边为外力功率。其中断裂能释放率可以由裂缝端部的J积分［90］求得。式（1-69）给出的能量平衡是用微观位移u［1］表示的，经过一系列积分变换，Dascalu et al［87］建立起了损伤演化与宏观状态量之间的关系如下

然后，将均匀化理论的形式解式（1-56）代入宏观能量平衡式（1-70），再经过一系列数学变换，可得如下损伤演化方程

其中4阶张量B的分量表达式为

Dascalu et al［87］利用得到的损伤演化表达式对某些实际结构进行了数值模拟。表明多尺度损伤演化表达式能够很好地联系宏观尺度结构的非线性行为及微观尺度微裂缝的产生和扩展。同时数值模拟的结果还表现出了显著的尺寸效应（size effect）［91］，即所得多尺度损伤演化依赖于单元体几何尺寸的变化，这与非线性断裂力学的研究结论［92］具有一致性，也从一个侧面验证了模型的正确性。

Dascalu多尺度损伤模型着眼于细观微裂缝的演化，将均匀化方法直接应用于带有微裂缝的单元体，采用能量作为联系宏观性能和细观微裂缝演化的工具，为多尺度损伤力学的研究提供了非常有价值的思路。然而，这一模型过于简单地采用裂缝的几何尺寸定义损伤变量，由此得到的损伤演化并不能直接应用于宏观结构的分析，而是还需要进一步求解等效材料刚度张量作为结构分析的依据。从本质上而言，这样的处理方式并没有将损伤力学实质性地引入多尺度分析的框架里面来，更没有发挥损伤力学在结构非线性模拟中的优势。