多尺度均匀化理论研究成果

均匀化理论（homogenization theory）的提出源于对复合材料等效性质的研究。在复合材料结构的分析和计算中，往往倾向于用等效的均匀材料代替复合材料，而等效均匀材料的性质需根据原始复合材料的结构求解得到。早期的方法大多直接立足于实际应用，并不具备严格的数学力学基础，但是却能够给出令人满意的结果。上世纪70—80年代期间，大量研究者深入研究了这一类复合材料求解方法，并且逐渐形成了具有严格数学基础的方法体系，最终形成了经典均匀化理论。关于经典均匀化理论的详细讨论，可参阅Bensoussan et al［57］以及Bakhvalov and Panasenko［58］的专著，这里对重要结论作简要回顾。

经典均匀化理论的建立基于周期性假定，即认为复合材料结构具有周期性微观结构（图1-6）。换言之，就是假定材料性质是整体空间坐标的周期性函数，函数的周期长度远小于整体结构的尺度。那么我们就可以将结构尺度看作宏观尺度，用宏观坐标x描述；而将微结构的周期长度看作微观尺度，用微观坐标y描述。二者之间的换算基于尺度参数∈，有

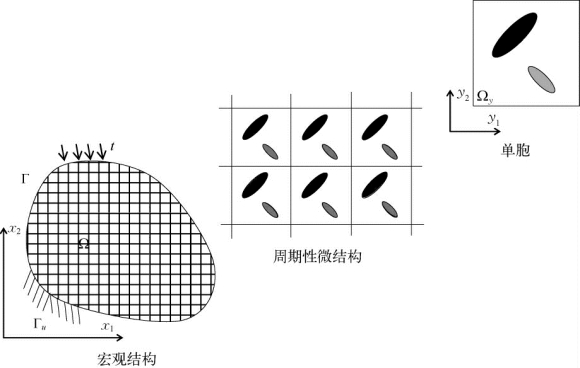
图1-6　周期性复合材料结构

定义在周期性微结构上的场函数，可以由统一尺度表达式展开为两尺度函数的摄动级数。对于位移场，有

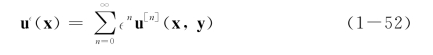
对于位移场求空间偏导数，可得应变场的摄动展开，有

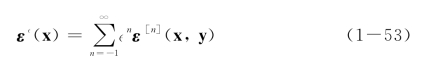
各阶应变分量

其中，⊗为张量算符的并乘；对称梯度算符。

对于线弹性材料，式（1-53）两边同乘以刚度张量C，可得应力的摄动展开如下

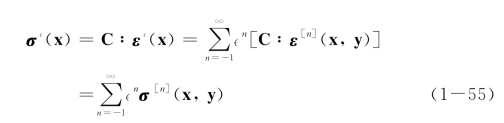
将应力摄动展开式（1-55）代入平衡方程，经过一系列数学处理［58］，可得位移场的0阶和1阶形式解如下

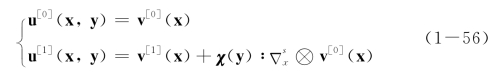
其中，v［0］（x）是宏观结构的位移场，此处可知位移场的0阶摄动解只与结构的宏观位移场有关，与微观坐标无关；v［1］（x）表征了单胞的空间平移对称性；3阶特征张量χ（y）表征了宏观响应与微观响应之间的变换关系，可由下述特征方程求解得出(www.xing528.com)

将形式解式（1-56）代入应变-应力的摄动展开式（1-53）和式（1-55）并截断高阶项，然后考虑单元体内的平均运算，可得均匀化刚度张量C表达式［58］如下

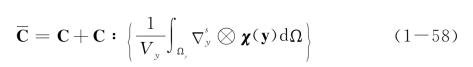
其中，Vy为单元体的体积；表示单元体内的平均。

至此可知，复合材料的均匀化刚度并不是其各组分刚度的直接平均，而与其特征张量χ（y）密切相关。

上述经典均匀化方法体系具有严格的数学基础，给出了复合材料等效性质求解的一般性理论体系，在实际中得到了广泛的应用。另一方面，经典均匀化方法也不可避免地存在某些局限。首先，实际的复合材料并不都具有周期性微结构，从理论上讲，经典方法是不适用于这一类材料的。其次，经典方法只得到了位移场的0阶和1阶摄动解，对摄动展开的高阶项进行了截断处理，这就使得在某些情况下经典方法的误差将会较大；再次，多尺度特征方程式（1-57）的求解是比较复杂的，对于一般的复合材料结构，很难得到解析解；最后，对于非线性材料或者演化的复合材料结构，经典均匀化方法将不再适用。对于这几个问题的探索构成了均匀化方法的最新发展，下文中将对各个方向上的发展逐一简述。

在实际应用中发现，将经典均匀化方法应用于某些非周期材料也能得到很好的结果。因此，可以考虑放松周期性假定，扩展经典均匀化方法的适用范围。经典均匀化方法之所以引入周期性假定，是为了获得数学处理上的便利，以期能够以代表性单元体表征复合材料的微结构性质。当然，代表性单元体的定义并不一定基于严格的周期性假定。最早Bensoussan et al［57］讨论了放松周期性假定的可能性，引入了“拟周期”（almost periodic or quas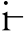periodic）结构的概念，将周期性从整体结构放松到局部结构，讨论了二阶拟周期椭圆型边值问题。曹礼群、崔俊芝［59］进一步讨论了二维、三维拟周期弹性结构的均匀化理论。Lions and Souganidis［60］建立了二阶退化偏微分方程在周期和拟周期条件下的均匀化理论。20世纪70年代以来，一些研究者完全放弃了周期性假定，转而从随机性的角度来描述复合材料微结构。Kozlov［61］以及Papanicolaou and Varadhan［62］最早研究了线性椭圆算子的随机均匀化，而后续的研究逐渐将随机均匀化应用于各类问题［63-67］。这些研究通过引入适当的概率空间，证明了如果材料的微结构性质满足有界性（bounded）、正定性（positive definite）、均匀性（stationarity）和各态历经性（ergodic），那么古典均匀化方法的结论在随机性微结构上几乎处处成立（almost surely）［68］。

Gambin［69］最早研究了考虑高阶项的均匀化方法，并推导得到了如下均匀化应力与应变的关系

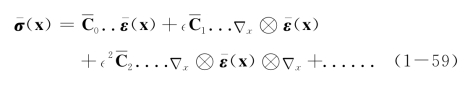
由上式可以发现，高阶摄动项的引入使得均匀化应力-应变关系发生了本质的改变，应力不仅与应变有关，还与应变的空间梯度有关。这与应变梯度理论（strain gradient theory）［70-72］的结论是一致的，同时应变梯度理论又被证明与非局部化理论（nonlocal theory）［73-75］具有某种程度的等价性。由此可知，考虑高阶项的均匀化理论可构成应变梯度理论与非局部化理论的理论基础。后来，Smyshlyaev and Cherednichenko［76］基于高阶均匀化理论严格推导出了应变梯度理论；而Boutin［77］则讨论了高阶均匀化理论与各类非局部化理论的关系。然而令人遗憾的是，高阶项的保留使得均匀化理论的表达、推导以及数值模拟都异常复杂，因此可以说高阶均匀化理论的理论意义远大于其实用意义。

Guedes and Kikuchi［78］较为系统地研究了经典均匀化方法的数值算法。为了便于数值分析和建模，Guedes and Kikuchi建立了均匀化方法的等价弱形式，其中特征方程（1-57）的等价弱形式表达式为

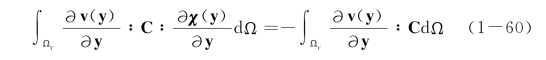
其中，v（y）为权函数。

基于式（1-60），可以应用标准的有限单元法流程数值求解材料特征张量χ（y）。为了提高数值模拟的精度和收敛速度，Guedes and Kikuchi［78］还讨论了自适应有限元方法在均匀化方法的应用。研究结果表明，由于复合材料内部各组分之间的弹性模量存在较大差异，自适应加密网格能够较好地模拟由此引起的应力集中，进而提高均匀化材料性质的计算精度。除了有限单元法，Chen and Mehraeen［79］尝试采用无网格（meshfree）方法进行了均匀化方法的数值分析研究。

非线性均匀化方法的研究总体上来说有两类基本思路。一类思路倾向于保证理论体系在数学上的严密性，将系统的控制方程考虑为某一类非线性方程，进而针对特定的非线性控制方程建立对应的均匀化理论。Evans［80］研究了哈密顿-雅可比（Hamilton-Jacobi）方程以及非线性椭圆方程的均匀化问题。Marchi［81］对非线性抛物线方程的均匀化问题进行了分析。Caffarelli et al［82］讨论了平稳各态历经介质中的非线性椭圆方程和抛物线方程的均匀化问题。之后，Camilli and Marchi［83］又进一步讨论了非线性椭圆方程均匀化理论的收敛性和收敛率。由于宏观结构的非线性响应非常的复杂，很难用一个方程完全的描述。这就使得上面的这一类研究还大多停留在数学层面，很难直接应用于工程实际。另一类思路则倾向于探求非线性产生的物理机理，将古典均匀化方法的结论直接应用于非线性演化的微结构。在这种思路的指导下，考虑微观裂缝的产生和发展，并采用均匀化方法的结果求解宏观等效材料性质，导致了多尺度损伤理论，这部分内容将在下一小节中做简要回顾。