基于多尺度分析的混凝土损伤演化研究

在动力加载条件下，需考虑混凝土的应变率效应。现有的连续损伤力学方面的研究大多倾向于利用静力损伤理论的框架，直接引入率相关的损伤演化函数，从而建立动力连续损伤力学体系。在连续介质损伤力学框架内，损伤演化方程可以统一表示为

其中，f±为损伤势函数。

对于静力损伤演化情况，损伤一致性因子可以由一致性条件求出；对于动力加载情况，为了考虑材料的率敏感性，Simo and Ju［22，28］参照粘塑性力学的处理技巧，直接引入损伤一致性因子的经验表达式如下

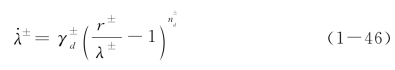
式中，均为控制动力损伤演化的材料参数。

上述处理方式虽然能够简单地将动力损伤演化与静力损伤演化统一起来，但是动力损伤演化的求解还是需要处理隐式非线性方程，这大大增加了结构模拟的计算量。1996年，Cervera et al［54］进一步改进了上述动力损伤演化表达式，给出了显式动力损伤演化方程，即

式中，为动力损伤驱动力，而r±为静力损伤驱动力，一般取为损伤能释放率或其单调函数。

动力作用下混凝土的细观损伤研究非常少。在既有研究中，Eibl and Schmidt-Hurtienne［55］借助前述微弹簧模型的基本思路，对黏弹性模型进行了推广。在Eibl的工作中，首先引入质量元件描述动力加载的局部惯性力效应，然后用质量元件、弹簧元件以及摩擦元件组成基本受力元件，最后将多个服从某种概率分布的基本受力元件并联，用以建立混凝土材料单轴受力的率相关模型（图1-5）。在这个模型中，混凝土的损伤可以用上述并联弹簧束的断裂表示，在弹簧断裂后，由于质量、黏性和摩擦元件的作用，应力不会立即降为0，而是存在一个应力释放和衰减的时间过程，基于此得到下述单轴动力本构方程(www.xing528.com)

图1-5　Eibl模型示意

其中静态损伤演化函数取Weibull分布函数

其中，a为形状参数，ε0为初始损伤阈值。Dfr（ε）表示弹簧断裂后内摩擦力的随机分布，也取为Weibull分布

b为形状参数。衰减函数g（t-τ）可取为指数函数形式或者直线函数形式。

上述模型从混凝土率效应产生的物理机理出发，分别采用不同的元件来描述细观层次上的黏性效应、惯性效应和微裂缝演化效应，并基于此建立了微观动力方程。但是，在从微观到宏观的建模过程中，该模型仅仅简单地用极值分布来代替损伤演化，并不能描述损伤演化的随机性，亦不能说明率效应对损伤演化随机性的影响。