混凝土随机损伤本构理论研究成果

在Kachanov［7］，Robotnov［8］，Lemaitre and Chaboche［9］等人的早期研究基础上，到20世纪70年代中期，损伤力学的理论框架逐步形成。1972年，Hult正式提出了损伤力学（damage mechanics）这一概念［10］。1981年，在法国召开了损伤力学的第一次国际会议。20世纪80年代以来，损伤力学引起了各国学者的广泛兴趣，得以迅速发展，并在实际工程中得到越来越广泛的运用。

一般认为，最早将损伤力学的基本概念应用于描述混凝土非线性特性的是Dougill［11］。但是，混凝土损伤力学理论研究中第一个具有开创意义的工作是Ladeveze和Mazars做出的［12-14］。众所周知：混凝土最典型的性质是其在拉应力和压应力作用下表现出迥异的强度与刚度特性（所谓单边效应）。为了考虑单边效应，Ladeveze［12］最先引入应力张量的正负分解

并假设由正应力引起受拉损伤，负应力引起受压损伤，在复杂加载时，损伤为受拉损伤和受压损伤的组合。

1984年，Mazars［13］进一步引入了等效单轴应变建立经验损伤演化方程，形成了针对混凝土材料的各向同性损伤模型。

根据Lemaitre等效应力假定，损伤材料的应力-应变关系可以定义为

其中，E0为未损伤材料的弹性模量，D为标量损伤变量。

与Ladeveze［12］相类似，Mazars认为损伤变量D可以表示成受拉损伤变量DT和受压损伤变量DC的线性组合

并将经验的损伤演化方程取为

式中，AT，AC，BT，BC和ε0均为材料常数。

显然，这一表述方式与混凝土一维受力的应力-应变关系有着强烈的关联。

线性组合系数αT和αC满足

Mazars建议的表达式为

其中，可由未损伤材料的应力（有效应力）计算给出。

在上述模型中，等效应变定义为

此处

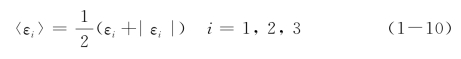
其中，｜·｜表示绝对值。事实上，等效应变的引入形成了多维受力本构关系的基础。

Mazars模型［13］虽然带有极强的经验性，但由于其等效应变表达形式具有简洁性和实用性，且损伤演化表达式（1-4）和式（1-5）具有高阶光滑性，从而有利于结构非线性分析的收敛。这一思路，对后续的混凝土损伤力学研究产生了深远影响。

1986年，Mazars［14］基于前述应力张量分解的思路，进一步引入弹性损伤能释放率建立损伤准则，为混凝土损伤力学的进一步发展奠定了基础。在这一研究中，Mazars认为材料的Helmholtz自由能势可表达为

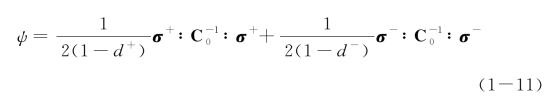
其中，C0为材料的弹性刚度张量；d+和d-分别为受拉损伤变量和受压（剪）损伤变量。

根据能量力学基本原理，对Helmholtz自由能势求偏导可得应力应变关系

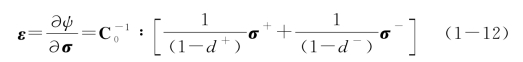
定义损伤能释放率为

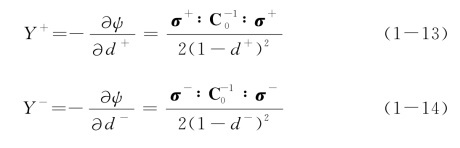
并将损伤演化方程表述为Y的函数，且仍采用与式（1-4）和式（1-5）类似的经验表达式

其中，A+，A-，B+，B-，以及均为材料常数。

上述模型具有较为坚实的热力学基础，能够很好地模拟混凝土材料在低周反复荷载作用下的刚度退化，分析结果与单轴试验结果的吻合程度也令人满意。

应力张量正负分解以及将与损伤变量对偶的损伤能释放率作为基本变量建立损伤演化法则的建模思路，对混凝土损伤力学的发展产生了深远的影响。上述模型，后来被称为Ledeveze-Mazars单边损伤本构模型［3］。

后续研究表明：Ledeveze-Mazars模型在本质上属于弹性损伤模型，并不能很好地反映多轴受压应力状态下混凝土强度和延性的提高。为此，不少研究者试图在弹性损伤的框架内修正和完善Ladeveze-Mazars模型，其中代表性的工作包括Mazars and Pijaudier-Cabot［15］、Lubarda et al［16］、Comi et al［17］、Papa and Taliercio［18］以及Comi and Perego［19］等。然而由于弹性损伤框架的局限性，上述模型并没有在Ladeveze-Mazars模型的基础上取得实质性进展，所建立的模型也很难很好地反映混凝土多轴非线性行为的机理和特性，尤其是在多轴受压区，模型预测结果与试验结果存在显著差距［20］。

弹性损伤模型的根本缺陷在于没有反映混凝土受力非线性发展过程中部分存在塑性变形这一事实。因此，自20世纪80年代中期以来，一批研究者试图突破弹性损伤的理论框架，将塑性应变及其演化规律引入到损伤本构关系的建模过程中，以期能够反映混凝土材料的残余变形。在此方向，研究工作大体上沿着两个侧面展开。其一是在Cauchy应力空间建立塑性应变的演化方程，如Ortiz［21］、Simo and Ju［22，23］、Lubliner et al［24］、Yazdani and Schreye［25］、Abu-Lebdeh and Voyiadjis［26］以及Carol［27］等。Cauchy应力表征宏观水平的表观应力，材料进入软化段后，宏观应力会产生下降，基于Cauchy应力空间建立的弹塑性损伤模型必然涉及屈服面收缩问题，因此会出现数值收敛和稳定性等一系列问题。而在另一侧面，在有效应力空间建立塑性应变演化方程，则不会出现这些问题。事实上，在加载过程中，有效应力空间内的屈服面一直处于膨胀状态而不存在收缩，因此可以避免软化段的复杂处理问题。在此侧面的典型研究见于Ju［28］、Lee and Fenves［29］、Faria et al［30］和Jason et al［31］等。

为了说明上述研究的脉络，需要先介绍有效应力的概念。在外力作用下，材料产生应变ε。对于已损伤材料，材料单元体上承担的应力就是结构对应点的实际应力，定义为柯西（Cauchy）应力σ；而与之对应的未损伤材料产生相同的应变ε后材料单元体上所承担的应力，就定义为有效应力σ-，如图1-2所示。(www.xing528.com)

图1-2　有效应力与柯西应力

实际上，如果将损伤理解为材料内部的微空洞和微缺陷，那么有效应力相当于作用在材料中除去空洞和缺陷之后的“净”面积上的应力。实际中，如果考虑材料的塑性变形，那么材料的总应变ε会包含弹性应变εe和塑性应变εp，即

此时有效应力定义为

为考虑单边效应，对有效应力张量也可以作正负分解，有

1998年，Faria et al［30］提出了基于有效应力分解的损伤能释放率表达式

由不可逆热力学原理，Faria et al［30］推导得到了损伤本构关系的基本表达式

基于有效应力分解的损伤能释放率表述，为在有效应力空间内处理塑性变形问题提供了方便与可能。但令人遗憾的是，为了较好地逼近试验结果，Faria et al［30］放弃了基于损伤能释放率建立损伤演化表达式这一途径，转而完全根据经验人为地定义了所谓“等价应力”，即

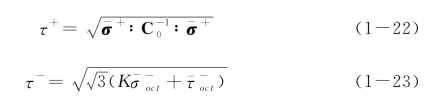
其中，为八面体上有效应力负分量；K为材料参数，用以描述混凝土二维受压加载下的抗压强度提高。

Faria et al［30］根据上述“等价应力”的定义，同时对损伤演化函数表达式（1-4）和表达式（1-5）进行了适当调整，给出了下述损伤演化表达式

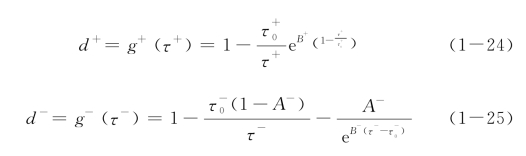
显然，这种损伤变量演化法则依然带有极强的经验痕迹。

对于塑性应变演化的处理，是建立弹塑性损伤模型时需要考虑的另一个重要问题。原则上，可以采用经典塑性力学中的类似手法处理这一问题，但是考虑到直接运用塑性力学方法在屈服状态判断时需要进行迭代，出于大型结构非线性分析时的计算效率考虑，不少学者主张采用经验表达的方法来考虑塑性变形，如Resende［32］，Faria et al［30］，Valliappan et al［33］和Hatzigeorgioiu et al［34］。其中Faria et al［30］建议的经验塑性应变率表达式为

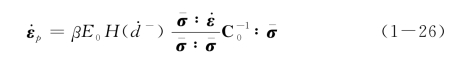
式中，β为经验系数；H（·）为Heaviside函数。

Valliappan et al［33］根据有效应力张量的定义，在应变主轴方向考虑塑性变形，认为塑性变形为主轴方向历史最大变形的δ倍，即

上述两个经验塑性模型均在弹塑性损伤建模中得到了广泛的应用。

损伤力学的核心问题之一是如何建立合理的损伤准则和损伤演化法则。在上述损伤本构模型中，基于损伤能释放率建立损伤准则（如Mazars弹性损伤本构模型［14］、Simo-Ju弹塑性损伤模型［22，23］等）虽然具有明确的不可逆热力学基础，但分析结果无法准确模拟混凝土的力学行为；而基于经验建立损伤准则（如Resende模型［32］、Faria模型［30］等）虽然可以较好地模拟混凝土的力学行为，但理论框架缺乏热力学基础，从而使其普遍性受到质疑。针对这一困境，吴建营、李杰从考虑损伤和塑性的耦合效应入手，引入弹塑性Helmholtz自由能势，基于损伤能释放率建立损伤准则，形成了具有热力学基础的双标量弹塑性损伤模型［20，35-39］。

为了考虑塑性耗散，可将Helmholtz自由能势分解为弹性和塑性部分

其中弹性Helmholtz自由能势为

而塑性Helmholtz自由能势ψp只与塑性变量κ以及受剪损伤变量d-有关，表示为

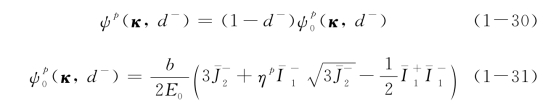
式中，为有效受压偏应力的第二不变量；的第一不变量；的第一不变量；b为材料参数，可根据实验确定。

与损伤变量对偶的损伤能释放率表达式为

类似于Mazars的猜测，在吴-李模型中，损伤演化法则取为

式中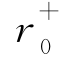，和为初始受拉和受剪损伤能释放率阈值；r+和r-为即时受拉和受剪损伤能释放率；A+，A-，B+和B-均为模型参数，可以根据试验得到的混凝土单轴受拉和单轴受压应力-应变曲线标定。

对比研究表明：应用吴-李模型的数值算法相对简单，计算效率能够满足大型混凝土结构非线性分析的需要。从而，在理论性和实用性上取得了较好的统一。但是，虽然通过引入弹塑性损伤能释放率，在损伤准则建立上奠定了热力学基础，但损伤演化法则仍然在本质上带有经验色彩。事实上，在宏观连续介质力学框架中，是难于在物理本质上揭示损伤演化规律的［2］。