大体积混凝土内外约束裂缝控制施工计算-高层建筑施工

1）大体积混凝土自约束裂缝控制施工计算

浇筑大体积混凝土时，由于水化热的作用，中心温度高，与外界接触的表面温度低，当混凝土表面受外界气温影响急剧冷却收缩时，外部混凝土质点与混凝土内部质点之间相互约束，使表面产生拉应力（图8.4）。由于温差产生的最大拉应力和压应力可由下式计算：

式中　σt、σc——混凝土的拉应力和压应力，N／mm2；

α——混凝土的线膨胀系数，℃－1，取1.0×10℃－5；

ΔT1——混凝土截面中心与表面之间的温差，℃；

ν——混凝土的泊松比，取0.15～0.2。

上两式中的混凝土的弹性模量Et按式（8.3）计算：

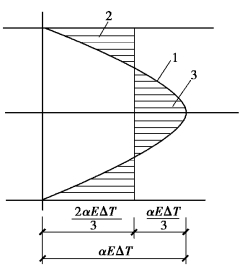
图8.4　内部温差引起的温度应力

1—温度分布；2—温度拉应力；3—温度压应力

式中　Ec——混凝土的最终弹性模量，N／mm2，可近似取28 d的混凝土弹性模量，可按表8.1取用；

e——常数，为2.718；

t——龄期，d；

β——混凝土中掺合料对弹性模量的修正系数，β＝β1·β2。

其中β1、β2为混凝土中掺粉煤灰和矿渣粉的掺量对应的弹性模量修正系数。当掺量分别为0、20%、30%、40%时，β1（掺粉煤灰）为1、0.99、0.98、0.96；β2（掺矿渣粉）为1、1.02、1.03、1.04。

表8.1　混凝土的弹性模量

注：①当有可靠试验依据时，弹性模量值也可根据实测数据确定；
②当混凝土中掺有大量矿物掺合料时，弹性模量可按规定龄期根据实测值确定。

由式（8.1）可知，如果σt小于该龄期混凝土的抗拉强度，则不会出现表面裂缝，否则有可能出现裂缝。同时，由式（8.1）、式（8.2）知，采取措施控制温差ΔT1就可有效地控制表面裂缝的出现。大体积混凝土一般允许温差宜控制在20～25℃。

若式（8.1）考虑混凝土徐变作用，应乘以S（t）。当结构的变形保持不变时，结构内的应力因徐变而随时间衰减的现象称为松弛。在计算温度应力时，徐变所导致的温度应力松弛有利于防止裂缝的开展。徐变可使混凝土的长期极限抗拉值增加1倍左右，提高了混凝土的极限变形能力。因此，在计算混凝土的抗裂性时，需要把松弛考虑进去。其松弛程度同加荷时混凝土的龄期有关，龄期越短，徐变引起的松弛越大。混凝土考虑龄期及荷载持续时间的应力松弛系数见表8.2。

表8.2　混凝土考虑龄期及荷载持续时间的应力松弛系数

2）大体积混凝土外约束裂缝控制施工计算

大体积混凝土基础或结构浇筑后，由于水泥水化热使混凝土温度升高，体积膨胀，达到峰值后（3～5 d）将持续一段时间，因内部温度先要慢慢与外界气温相平衡，之后温度将逐渐下降，从表面开始慢慢深入到内部时混凝土已基本结硬，弹性模量很大，降温时温度收缩变形受到外部边界条件的约束，将产生较大的温度应力。一般混凝土内部温升值越大，产生的拉应力也越大，如通过施工计算采取措施控制过大的降温收缩应力出现，即可控制裂缝的发生。外约束裂缝控制的施工计算按不同时间和要求，分以下两个阶段进行：第一阶段是混凝土浇筑前裂缝控制；第二阶段是混凝土浇筑后裂缝控制施工计算。下面仅讲述第一阶段。

在大体积混凝土浇筑前，根据施工拟采取的施工方法、裂缝控制技术措施和已知施工条件，先计算混凝土的最大水泥水化热温升值、收缩变形值、收缩当量温差和弹性模量，然后通过计算，估量混凝土浇筑后可能产生的最大温度收缩应力。如小于混凝土的抗拉强度，则表示所采取的裂缝控制技术措施，能有效地控制裂缝的出现；如超过混凝土的允许抗拉强度，则应采取调整混凝土的浇筑温度，降低水化热温升值及内外温差，改善施工操作工艺和性能，提高混凝土极限拉伸强度或改善约束等技术措施，再重新进行计算，直至计算的降温收缩应力在允许范围以内为止，以达到预防温度裂缝出现的目的。计算步骤和方法如下：

（1）混凝土的绝热温升值计算

混凝土的水化热绝热温升值，一般按下式计算：

式中　T（t）——浇完一段时间t，混凝土的绝热温升值，℃；

mc——每立方混凝土胶凝材料（水泥、粉煤灰等）用量，kg／m3；

Q——每千克胶凝材料（水泥、粉煤灰等）水化热量，kJ／kg，可查表8.3求得；

C——混凝土的比热容为0.92～1.0 kJ／（kg·K），一般取0.96 kJ／（kg·K）；

ρ——混凝土的质量密度，取2 400～2 500 kg／m3；

e——常数，为2.718；

t——龄期，d；

m——与水泥品种、比面积、浇捣时温度有关的经验系数，由表8.4查得，一般取0.3～0.5 d－1。

表8.3　水泥在不同期限内的发热量

注：本表按平均温度为＋15℃编制的，当硬化时的平均温度为7～10℃，则Q值按表内数值。

表8.4　计算水化热温升时的m值

实际大体积混凝土基础或结构外表是散热的，混凝土的实际温升低于绝热温升，计算值偏于安全。

（2）各龄期混凝土收缩变形值的计算

混凝土在水泥水化、胶凝、硬化及随后的碳化过程中，必将引起体积的收缩，将产生一定的收缩变形。

各龄期混凝土的变形值—般可按下式计算：

式中　——标准状态下的最终收缩值（即极限收缩值），取（3.24～4.0）×10－4；

εy（t）——非标准状态下混凝土龄期为t时的收缩引起的相对变形值；

e——常数，为2.718；

b——经验系数，取0.01；

t——龄期，d；

M1，M2，M3，…，M11——考虑各种非标准条件，以及与水泥品种细度、骨料品种、水胶比、水泥浆量、养护条件、环境相对湿度、构件尺寸、混凝土捣实方法、配筋率等有关的修正系数，按表8.5取用。

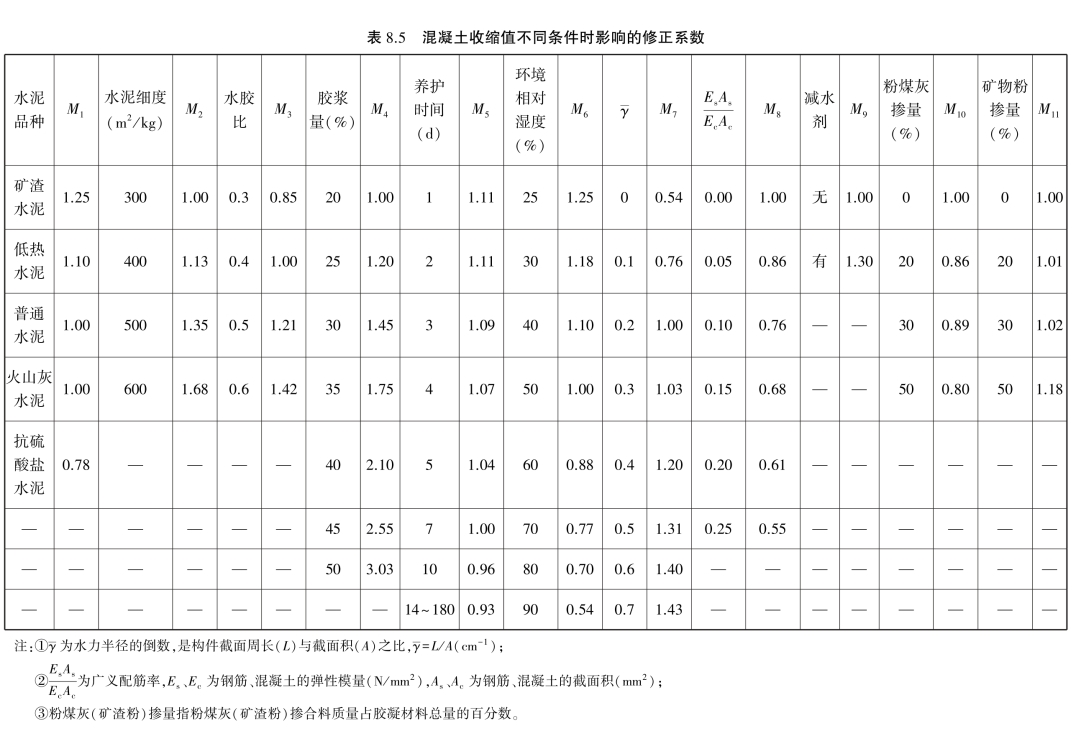
（3）混凝土收缩当量温度计算

混凝土的收缩当量温度是将混凝土干燥收缩与自身收缩产生的变形值，换算成相当于引起等量变形所需要的温度，以便按温差计算温度应力。

混凝土收缩变形会在混凝土内引起相当大的应力，温度应力计算时应把混凝土收缩变形这个因素考虑进去。为方便计算，将混凝土收缩变形合并在温度应力之中换成当量温度，按下式计算：

式中　Ty（t）——龄期为t时的混凝土收缩值当量温度；

εy（t）——各龄期混凝土的收缩相对变形值；(www.xing528.com)

α——混凝土的线膨胀系数，℃－1，取1.0×10－5。

（4）各龄期混凝土弹性模量计算

变形变化引起的应力状态随弹性模量的上升而显著增加，计算温度收缩应力应考虑弹性模量的变化，各龄期混凝土弹性模量可按式（8.3）计算。

（5）混凝土温度收缩应力计算

大体积混凝土基础或结构（厚度大于1 m）贯穿性或深进的裂缝，主要是由平均降温差和收缩差引起过大的温度收缩应力而造成的。混凝土因外约束引起的温度（包括收缩）应力（二维时），一般用约束系数法来计算约束应力，按以下简化公式计算：

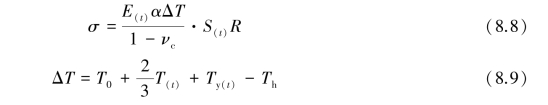
式中　σ——混凝土的温度（包括收缩）应力，N／mm2；

E（t）——混凝土从浇筑后至计算时的弹性模量，N／mm2，一般取平均值；

α——混凝土的线膨胀系数，℃－1，取1.0×10－5℃－1。

ΔT——混凝土的最大综合温差，℃，当大体积混凝土基础长期裸露在室外，且未回填土时，ΔT值按混凝土水化热最高温升值（包括浇筑入模温度）与当月平均最低气温之差进行计算；

T0——混凝土的入模温度，℃；

T（t）——浇筑完一段时间t，混凝土的绝热温升值，℃，按式（8.4）计算；

Ty（t）——混凝土收缩当量温差，℃，按式（8.7）计算；

Th——混凝土浇筑完达到稳定时的温度，一般根据历年气象资料取当年平均气温，℃；

S（t）——考虑徐变影响的松弛系数，按照表8.2取用，一般取0.3～0.5；

R——混凝土的外约束系数，当为岩石地基时，R＝1，当为可滑动垫层时，R＝0，一般土地基取0.25～0.50；

νc——混凝土的泊松比，取0.15。

（6）控制温度裂缝的条件

①混凝土抗拉强度可按下式计算：

式中　ftk（t）——混凝土龄期为t时的抗拉强度标准值，N／mm2；

ftk——混凝土抗拉强度标准值，N／mm2，可按表8.6取值。

γ——系数，应根据所用混凝土试验确定，当无试验数据时，可取0.3。

表8.6　混凝土抗拉强度标准值单位：N／mm2

②混凝土抗裂性能可按下列公式进行判断：

式中　σ——大体积混凝土自约束或者外约束拉应力，MPa；

k——防裂安全系数，取1.15；

η——掺合料对混凝土抗拉强度影响系数，η＝η1η2，可按表8.7取值。

表8.7　不同掺量掺合料抗拉强度调整系数

【例8.1】　轧板厂大型设备基础混凝土采用C30，用32.5级普通硅酸盐水泥配置，水泥用量为345 kg／mm3，粉煤灰掺量为3.45 kg／m3，水灰比为0.52，混凝土坍落度为180～200 mm。Ec＝3.0×104 N／mm2，Ty＝9℃，S（t）＝0.3，R＝0.32。混凝土浇灌入模温度为14℃，当地平均温度为15℃，由天气预报知养护期间月均最低温度为3℃。试计算可能产生的最大温度收缩应力和露天养护期间（15 d）可能产生的温度收缩应力及抗裂安全度。

【解】（1）计算混凝土的绝热温升值

由表8.3可知Q＝335 kJ／kg，C＝0.96 kJ／kg，ρ＝2 400 kg／m3，混凝土15 d水化热绝热温度及最大的水化热绝热温度为：

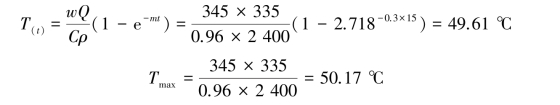
（2）计算各龄期混凝土收缩变形值

由表8.5知，M1＝1.0，M4、M7均为1，M2＝1.06，M3＝1.25，M5＝0.93，M6＝0.7，M8＝0.95。

则混凝土的收缩变形值为：

（3）计算混凝土的收缩当量温差

混凝土15 d收缩当量温差为

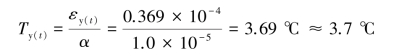
（4）计算各龄期混凝土的弹性模量混凝土

混凝土15 d弹性模量温差为：

（5）计算混凝土的温度收缩应力及抗裂判断

混凝土的最大综合温差为（T（t）取最大）：

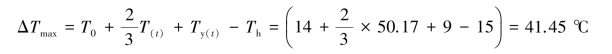
则基础混凝土最大降温收缩应力为（此处取E（t）最大）：

因为ftk＝2.01 N／mm2（取最大值），η＝1.015，k＝1.15。

代入公式σ≤ηftk（t）／k成立，即1.40 N／mm2≤1.015×2.01／1.15 N／mm2＝1.77 N／mm2，满足抗裂要求。

露天养护期间基础混凝土产生的降温收缩应力为（此处T（t）、E（t）、ftk（t）均取第15天的值）：

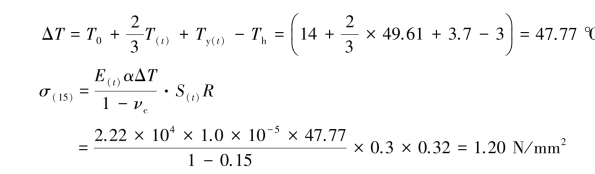
据式（8.10），混凝土的15 d抗拉强度：

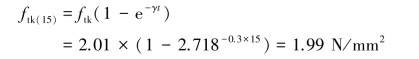
因为η＝1，k＝1.15，代入公式σ≤ηftk（t）／k成立，即1.20 N／mm2≤1.015×1.99 N／mm2／1.15＝1.76 N／mm2，满足抗裂要求。

假设计算结果不能满足抗裂要求，在此期间混凝土表面应采取养护和保温措施，使养护温度加大（即Th加大），综合温差ΔT减小，使计算的σ（15），满足σ≤ηftk（t）／k的要求，则可控制裂缝出现。