平面体是由若干个平面多边形围成,各表面的交线称为棱线,棱线也是各表面的边界线,又是各表面的轮廓线。常见的平面体有正方体、长方体、棱柱、棱锥、棱台;把正方体、长方体称为长方体,把棱柱、棱锥、棱台称为斜面体,如图1-10所示。
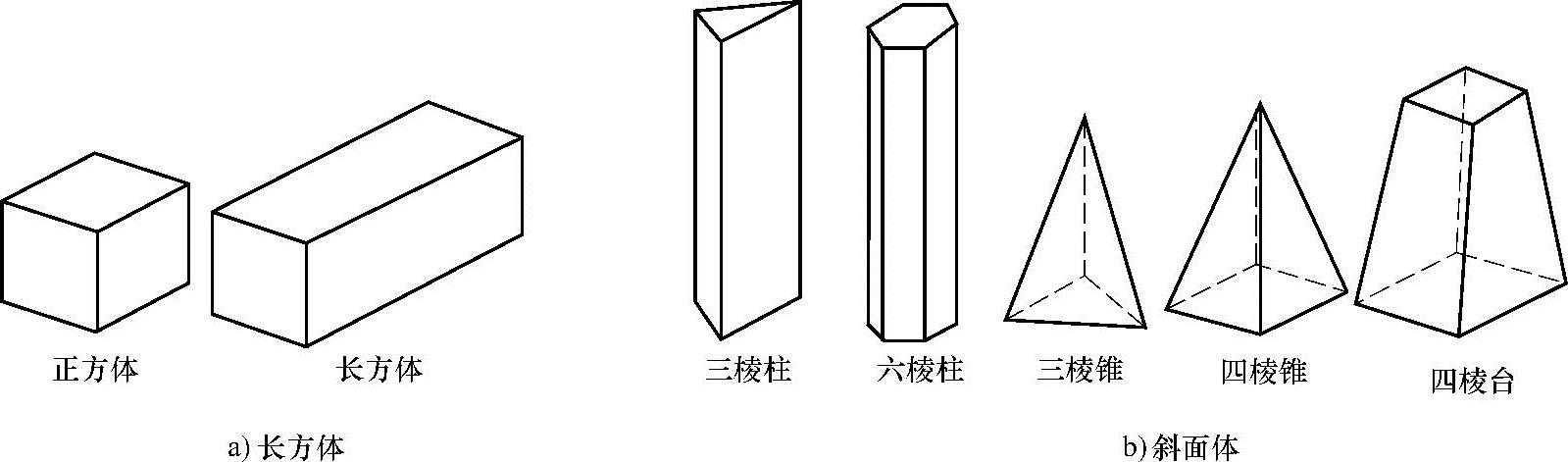
图1-10 平面体
1.长方体的投影
长方体是由互相平行的长方形上下底平面和四个长方形侧面所围成。将长方形放在三投影面体系中,方向摆正,即长方体前后两个平面与正立面(V面)平行,左右两个平面与侧立面(W面)平行,上下两个平面与水平面(H面)平行,如图1-11a所示。
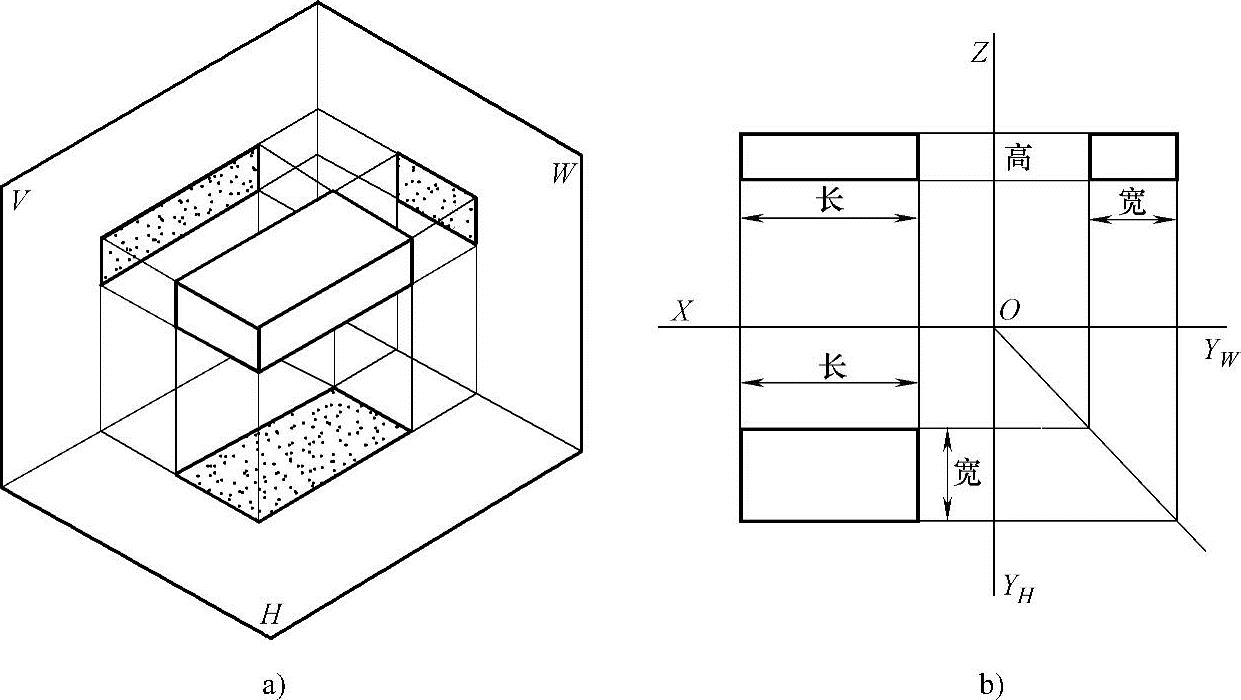
图1-11 长方体的投影
长方体在V面投影是一个长方形,反映了长方体的长和高;长方体在H面上的投影是一个长方形,反映了长方体的长和宽;长方体在W面上的投影也是一个长方形,反映了长方体的宽和高。三个投影分别反映了长方体中三个向度中的两个向度,只有综合分析三个视图,才能知道长方体的三个向度,其三面投影如图1-11b所示。主视图反映长和高,俯视图反映长和宽,左视图反映高和宽,画图时,应掌握各视图之间的这种关系,即:
1)主视图和俯视图,长对正。
2)主视图和左视图,高平齐。(https://www.xing528.com)
3)俯视图和左视图,宽相等。
这就是三投影体系中三个视图的关系和画法要点。三等关系对以后所讲的体的投影同样适用。
2.棱锥体的投影
棱锥体是由一个多边形底面和若干个具有公共顶点的三角形所围成。若底面为正多边形,顶点位于底面中心的正上方,称为正棱锥。以底面为正四方形的正四棱锥为例,如图1-12a所示。
将正四棱锥置于三投影面体系中,使其底面平行于H面,左右两个侧面垂直于V面,前后两个面垂直于W面,对其进行三面投影。由图1-12b可见,它在V面上的投影是一个等腰三角形线框,表明正四棱锥前后两个棱面在V面上投影的重迭,由于这两个平面都倾斜于V面,所以其投影是小于实形的平面。三角形线框各边是左右两个侧面和底面在V面上投影的积聚。
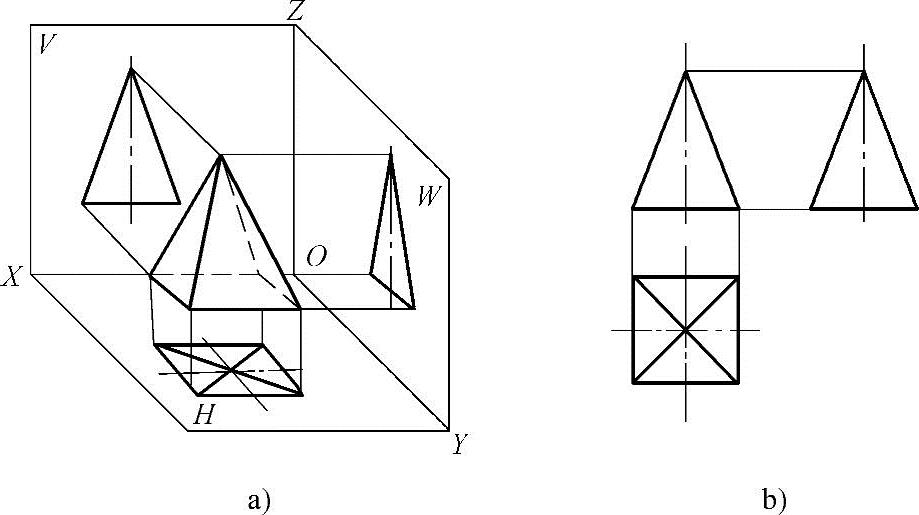
图1-12 正四棱锥的投影
在H面上的正四棱锥投影是由四个三角形组成,外形为四边形线框,四边形线框反映了四棱锥底面的实形,四个三角形是正四棱锥四个侧面的投影,由于各侧面都倾斜于H面,所以四个侧面的投影都是小于实形的平面。四个三角形的各边是四个侧面棱边的投影。
正四棱锥在W面上的投影也是一个三角形线框,它反映了正四棱锥左右两个侧面和底面的投影,两侧面投影具有重叠性,底面投影具有积聚性。由于两侧面都倾斜于W面,所以投影都小于实形。三角形线框中的两条斜边是前后两个侧面的投影,而底边是底面的积聚投影。正四棱锥的三面投影,如图1-12b所示。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




