DCSK调制解调，应用于图像加密与智能交通光通信保密系统

1.DCSK 调制

图4-21 为DCSK 调制系统的模型图。在 DCSK 调制中，发送的每一比特信息的周期被平分为2 个时隙。在同一周期的第1 个时隙，发送器首先传输混沌序列，此混沌序列直接由混沌发生器产生且不携带任何信息，仅是作为信息传输的参考信号；在这一周期的第2 个时隙，发送方传输一段与参考信号长度相同的混沌序列，同样产生于混沌信号发生器，但会延迟β 长度之后，用于承载需要传送的二进制信息比特。当发送方传输的信息比特为“ +1”时，信息信号与参考信号完全相同；当发送方传输的信息比特为“-1”时，信息信号与参考信号互为反相[214]。其中传送信息的比特速率为1/β。

设第k 位比特信息为bk=｛-1,+1｝，由此可以得出这个通信系统在第k 个比特周期内传输信号的时域表达式为：

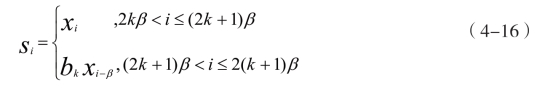
其中，β 表示混沌信号的采样点数，通俗地说就是参考信号中混沌序列的长度。扩频因子为扩频码的个数，在这里，扩频因子SF=2β。

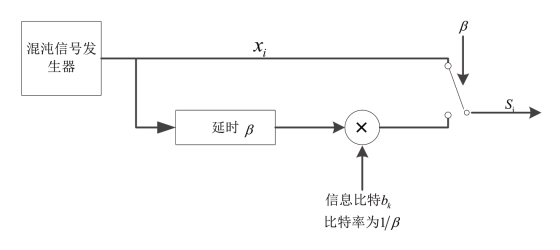
图4-21　DCSK 的调制模型

2.DCSK 解调

DCSK 非相干解调模型如图4-22 所示。信息到达接收方时需要对调制后的信号进行解调。为了解调出发送信息bk，接收方将接收信号 ri 与延迟 β 后的接收信号 ri-β 进行相关，再对信号进行门限判决，就可以得到原始的信息比特。

图4-22　DCSK 解调(www.xing528.com)

在信息调制后进入信道，会受到信道中噪声的干扰，如果在传输的过程中只受到加性高斯噪声的影响，则接收到信号为：

ni为服从高斯分布的随机变量。

则相关器的输出的Zk为

将式（4-17）代入式（4-18）可得：

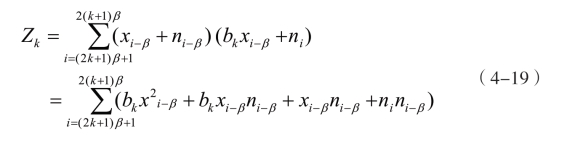
由式（4-19）可知，第1 项为混沌信号的自相关项（即有用信号分量），并且可以看出，第一项的正负取决于发送的比特信息，是有用信号；第2，3项为混沌信号和噪声信号的互相关项，为随机噪声，第4 项为噪声信号的互相关项。由于第2，3，4 项都是由信道中的噪声引起的，因此统称为噪声分量。再加上后三项的数学期望值为零，因此整体式子的正负只取决于第一项，此时需要恢复的信息比特就类似一个符号函数，因此可以设置门限判决为0。根据判决准则恢复比特信息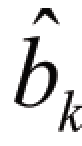，见公式（4-20）。

DCSK 采用混沌信号直接作为载波，由于混沌信号的非周期性，在不同的比特时间内，Zk第一项并不是固定不变的，而是在统计意义上随机分时间的延长逐渐趋于一个平均值（即DCSK 信号平均比特能量的1/2）。