混沌应用于图像加密和智能交通光通信保密系统

本系统采用AWGN 进行MATLAB 仿真。

（一）系统安全性分析

CPPM-N 调制系统表示混沌扩频码为N 的混沌扩频PPM 系统。N 分别取值为16，32，64，128，256，512 和1024，本文对同一混沌扩频码进行蒙特卡罗1000 次实验，信噪比为-7dB ~7dB，步长为1dB。随机发送长度为32bit 信息码。混沌序列对初始值非常敏感，即使密钥值有微小的变化也会得到完全不同的2 个混沌序列，不知密钥就很难进行解扩运算。扩频时所用Logistic 映射的初始值均（即密钥）为0.289999，解扩时所用Logistic 映射的初始值分别为0.289999 和0.289998 时得到CPPM-N 调制系误码率随着信噪比变化的曲线分别如图4-4（a）、图4-4（b）所示。从图4-4（b）可以看出，扩频与解扩时所用的初始值仅相差0.000001，CPPM-N 系统的误码率就很高，约为0.5，系统无法接收到正确的信息。因而本系统可保证传输信息的安全性。

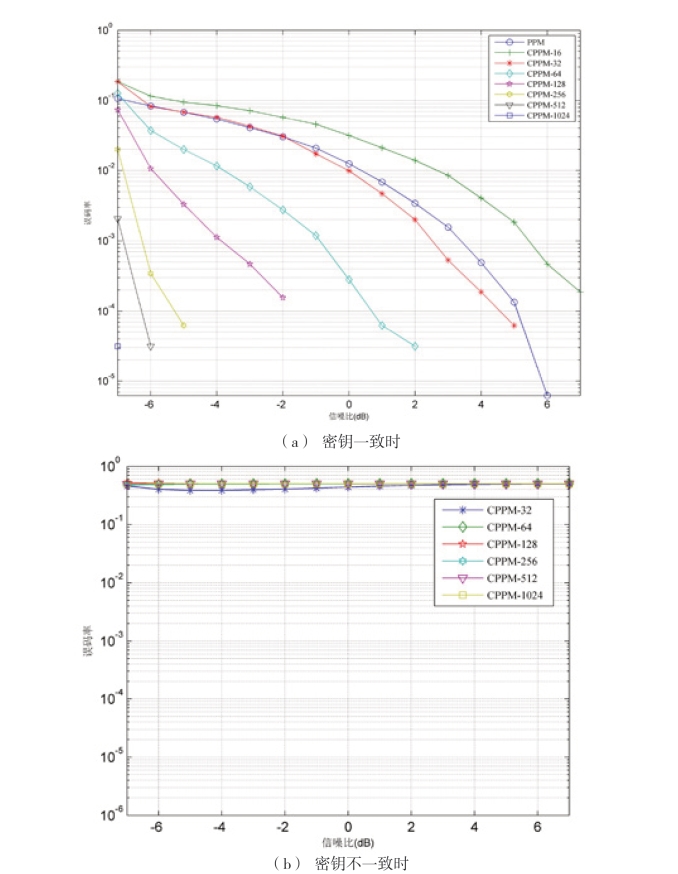
图4-4　信噪比S/N 与PPM 和CPPM 调制系统误码率BER 的关系曲线图

（二）密钥一致情况下系统误码率分析

1.在不同的信噪比下PPM 和CPPM-N 调制系统误码率分析

在PPM 系统和密钥一致CPPM-N 调制系统下，误码率随信噪比变化特性统计表如表4-1 所示。

表4-1　特定混沌序列长度N 下，PPM 系统和CPPM-N 调制系统的误码率随信噪比变化特性

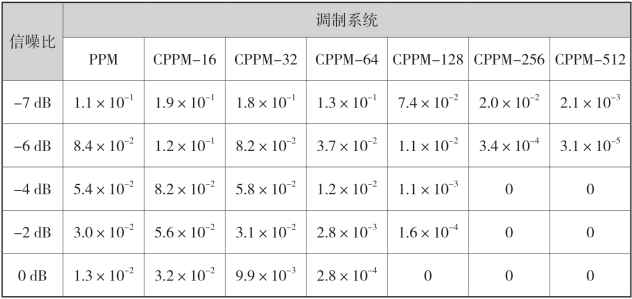
由图4-4（a）和表4-1 得出以下几点结论：

（1）随着信噪比的增加，PPM 系统和CPPM-N 调制系统误码率呈现逐渐下降趋势。

（2）信噪比为-7dB ~1dB 时，PPM 和CPPM-32 调制的误码率相近；信噪比为1dB~6dB 时，CPPM-32 调制的误码率比PPM 误码率低。在相同信噪比条件下CPPM-N 调制的误码率随着混沌扩频码N 的增加，误码率逐渐降低。(www.xing528.com)

（3）当混沌扩频码N小于32时，CPPM-N调制的误码率比PPM误码率高；当混沌扩频码N 大于32 时，CPPM-N 调制的误码率比PPM 误码率低。因此，将扩频引入到光通信系统可以降低系统误码率。

2.混沌扩频码长度和信噪比对CPPM 系统误码率影响

图4-5 为信噪比一定时CPPM 系统误码率随着混沌扩频码长度N 变化的关系曲线图。其中，扩频和解扩时所用Logistic 映射的初始值（即密钥）均为0.289999，信噪比分别取值-6 dB，-4 dB，-2 dB 和0dB，随机发送长度为32bit 信息码，对同一信噪比进行蒙特卡罗1000 次实验。

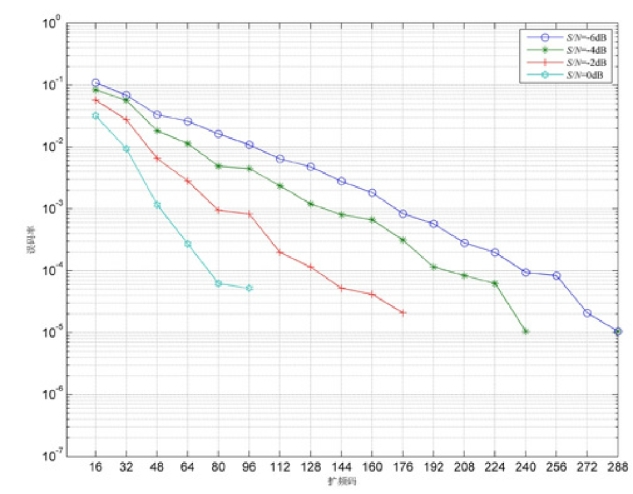
图4-5　特定的信噪比下，混沌序列长度N 与CPPM 系统误码率的关系图

在特定信噪比下，CPPM 系统的误码率随混沌序列长度N 变化特性如表4-2 所示。

表4-2　特定信噪比下，CPPM 系统的误码率随混沌序列长度N 变化特性

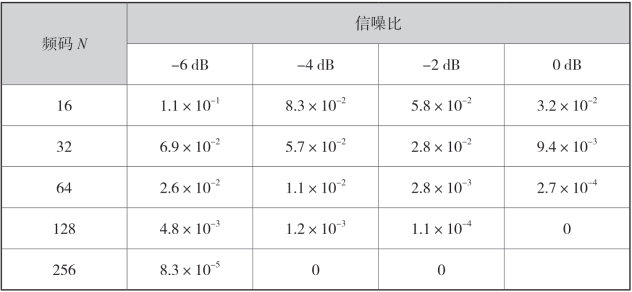
由图4-5 和表4-2 得出以下几点结论：

（1）当混沌序列长度N 一定时信噪比越大，CPPM 的调制系统的误码率越低。

（2）相同信噪比条件下，随着混沌序列长度N 增加，CPPM 的调制系统的误码率随之变小，但对信号发送和接收速率要求越高，对硬件性能要求也越高。因此，根据使用硬件性能情况和系统要求误码率来确定N 的长度。