小波变换是一种新的变换分析方法，它的主要特点是通过变换能够充分突出问题某些方面的特征，因此，小波变换在许多领域都得到了成功的应用，特别是小波变换的离散数字算法已被广泛用于许多问题的变换研究中。从小波变换的数学理论来说，它是继傅立叶变换之后纯粹数学和应用数学完美结合的又一光辉典范，享有“数学显微镜”的美称。从纯粹数学的角度来说，小波变换是调和分析（包括函数空间、广义函数、傅立叶分析和抽象调和分析等）这一重要学科大半个世纪以来的工作结晶；从应用科学和技术科学的角度来说，小波变换又是计算机应用、信号处理、图像分析、非线性科学和工程技术近几年来在方法上的重大突破[182-183]。
1.小波变换的定义
若ψ(x)是一个实值函数且它的频率ψ(s)满足容许条件
则ψ(x)被称为一个基本小波。同时满足：
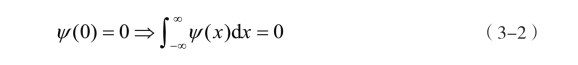
设其伸缩因子（又称尺度因子）为a ,平移因子b，一组小波基函数｛ψa,b(x)｝可通过平移和伸缩基本小波来生成：
小波变换的系数以被变换函数和每一基函数的内积形式给出，即函数f(x)以小波ψa,b(x)为基的连续小波变换为：
而连续小波变换的逆变换为：
2.小波变换的优点[184]
（1） 小波变换是一个能够满足能量守恒方程的变换，能够将信号分解成对空间和频率的独立贡献，同时又不丢失原信号所含的信息。
（2） 小波变换相当于一个具有放大缩小和平移功能的数学显微镜，通过检查不同的放大倍数下信号的变化来研究其动态特性。
（3） 巧妙利用了非均匀分布的分辨率，较好地解决了空间和频率分辨率的矛盾。
（4） 利用二维离散正交小波变换将原图像在度量的频带与不同的空间方向上进行分解，便于利用人眼视觉系统在响应频带与空间方向选择上敏感性的不同。
（5） 小波表示介于空间域与频率域之间，可同时提供空间和频率的信息。
3.二维离散小波变换
从滤波器的观点看，不同尺度下的小波函数可看作带通滤波器，尺度函数可看作低通滤波器，由此构成滤波器族[185]。信号的小波分解就是将信号通过一组分析滤波器族，从而将信号分解成低频和高频两个部分。信号的细节信息大部分集中于高频区域，而分解得到的低频部分又被分解成低频和高频部分，此过程反复进行直至满足信号分析的需求。这样信号各精度级的不同频率特性被分别保存，而且各频率分量之间是不重叠的。小波综合就是将信号通过一组综合滤波器，小波分解后的系数又可以重构原始信号，而构成原信号的过程称为小波反变换。
依据滤波器族的理论，满足一定条件的离散低通滤波器脉冲响应能够产生一个尺度函数。谈及二维离散小波变换，我们考虑二维尺度函数可分离的情况，即：
其中，Φ(x)是一个一维的尺度函数。
若Ψ(x)是一个小波，那么下面三个二维基本小波
式（3-7）、式（3-8）和式（3-9）就构成了二维小波变换的基础（这里使用的上标只是索引）。具体来说，函数集(www.xing528.com)
它们构成L2(R2)中的正交归一基。其中，j, m,n,α为整数，整数j 决定伸缩，m 和n 确定平移幅度，α 表示二维基本小波的上标索引。
图像可依据二维小波变换按如下方式展开。在小波正变换的每一层次中，图像都被分解成四个四分之一大小的图像，如图3-6 所示。这四个图像的每一个都是原图像与一个小波基的内积后，再经过在行和列方向都进行2 倍的间隔抽样而生成的。对第一层（设原图像f1(x,y)
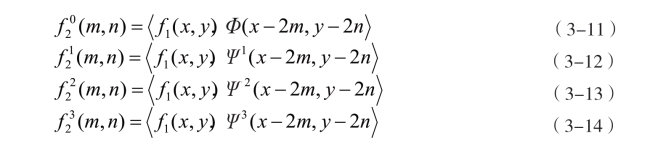
图3-6 二维离散小波变换
对于后继的层次（令j 表尺度的索引，j＞1），
(x,y)都以相同的方式分解而构成四个在尺度2 j+1上的更小的图像（将内积写成卷积的形式）：
并且在每一层次进行四个相同的间隔抽样滤波操作。因为尺度函数与小波函数都是可分离的，所以每个卷积都可以分解成在
(x,y)的行和列上与低通函数h0(- x)和高通函数h1(- x)的一维卷积。图3-7 显示了这个过程。
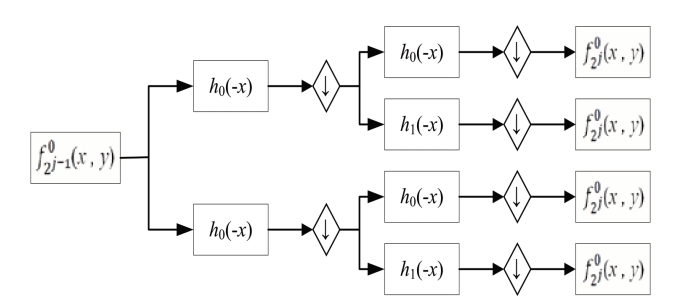
图3-7 DWT 图像分解步骤
在小波逆变换的每一层中，我们都通过在每一列的左侧插入一列零来增频采样前一列的四个阵列，接着用h0(- x)和h1(- x)进行卷积，再对所得的阵列成对相加就得到一次重建的和；然后通过在每行上插入一行零，将所得的和阵列增频采样，再用h0(- x)和h1(- x)与这两个阵列的每列卷积，所得阵列成对的和，即为这一层次重建的结果。这一过程可以从图3-8 清楚地看出来。
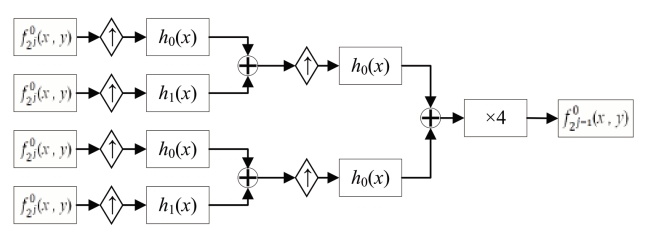
图3-8 DWT 图像重建步骤
图像数据的每一级小波分解总是将上级低频数据划分为更精细的频带，在对图像进行多级（M 级）小波分解后，将得到在一系列倍频程划分的频带上的多个高频带数据和一个低频带数据，这些高频带数据就是LHj,HLj,HHj(j =1,2,…,M)3个频带系列，低频带数据就是最后的。LLM频带，图3-9 显示了图像Woman 经3 级小波变换后的小波图像[61]。
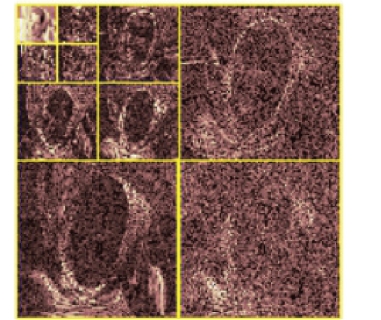
图3-9 Woman 的3 级小波分解图像
小波图像的各个频带分别对应了原图像在不同尺度和不同分辨率下的细节以及一个由小波变换分解级数决定的最小尺度、最小分辨率下对原图像的最佳逼近。。LLM频带是原图像的逼近，原图像的主要内容都体现在这个频带的数据中。小波图像的各个高频带是原图像中边缘、轮廓和纹理等细节信息的体现，并且各个频带所表示的边缘、轮廓等信息的方向是不同的，其中HLj表示了垂直方向，HLj表示了水平方向，而对角方向则集中体现在HLj 频带中。小波图像的各个频带之间并不是纯粹无关的，特别是对于各个高频带，由于它们是图像的同一个边缘、轮廓和纹理信息在不同方向、不同尺度和不同分辨率下由粗到细的描述，它们之间必然存在着一定的关系，其中很明显的是这些频带中对应边缘、轮廓的位置是相同的。在小波图像中，不为0 的系数主要集中在LL 低频带和各个高频带中对应图像边缘、轮廓和纹理位置的地方。对于一般的图像而言，这种边缘、轮廓和纹理是通常无序的。
4.常用小波
随着小波理论及各种数值算法的发展，人们在一些基本小波的基础之上，构造了满足不同需要的小波[186]，但常用的基本小波有Harr 小波、Daubechies小波（简写为DB）、Mexico 草帽小波、Morlet 小波、Meyer 小波、Symlets 小波、Coiflets 小波、Biorthogonal 双正交小波（简写为Bior.）。其性质如表3-1 所示，其中*表示此种小波具有对应的性质，—表示此种小波不具有对应的性质。
表3-1 小波性质
续 表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
