Tent映射特性及仿真：应用于智能交通光通信保密系统中

1. Tent 的初值敏感性

Tent 混沌系统具有初值敏感性的特征。式（2-20）中，A=1/2，B=1.9999，初始值z（0）分别为0.289999，0.290000，迭代次数为100，就可以得到Tent 映射的初始值敏感图，如图2-24 所示。横轴表示迭代次数n，纵轴表示序列的取值z（n）。

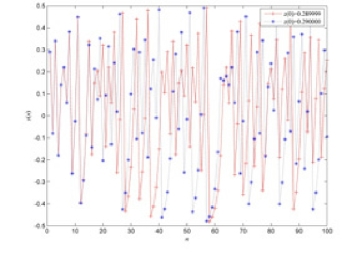
图2-24　Tent 的初始值敏感性

从图2-24 可以看出，两者的初始值仅相差10-6，刚开始迭代的两条曲线基本重合，但是经过一段时间的迭代后，两个曲线有很大的差别，这说明混沌序列对初始值非常敏感。通过预置初始值，可以产生不同的混沌序列，产生的序列数量非常多。

2. Tent 的遍历性

理论上，当z（n）经过n 次迭代运算后（n 值足够大时），其迭代运算值（zn）等遍历[ -0.5,0.5]上所有的值。取初始值A=1/2，B=1.9999，z（0）=0.289999，对式（2-20）进行1000 次迭代所产生的混沌轨迹如图2-25 所示。横轴表示迭代次数n，纵轴表示序列的取值z（n）。图中的“+”表示第n 次迭代运算值z（n）。从图2-25 中可以看出，当迭代次数足够大时，模拟混沌序列的取值z（n）几乎遍历了[ -0.5,0.5]的区间。

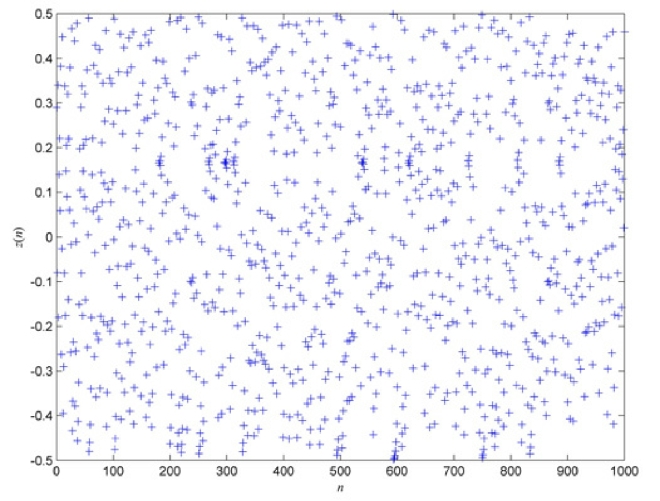
图2-25　Tent 的遍历性

3. Tent 的相空间

取初始值A=1/2，B=1.9999，z（0）=0.289999，迭代次数为1024，可以得到Tent 映射的二维相空间图（图2-26）和三维相空间图（图2-27）。

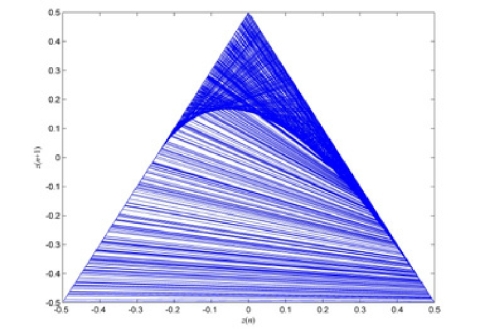
图2-26　Tent 的二维相空间

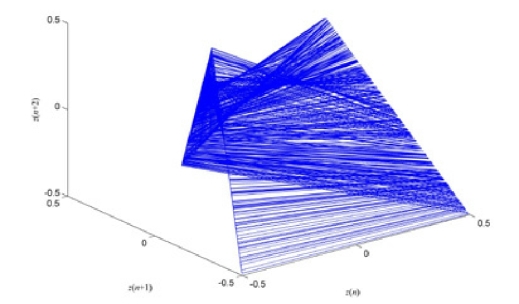
图2-27　Tent 的三维相空间

4.Tent 的相关性

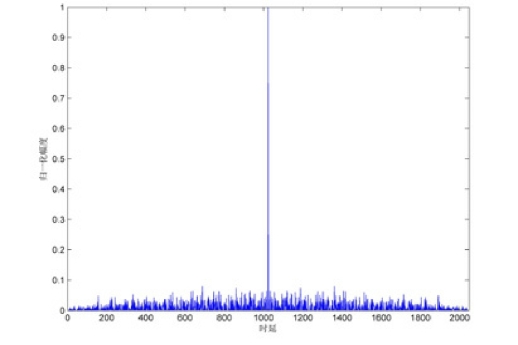
取序列长度N=1024，A=1/2，B=1.9999，z（0）=0.289999，相关间隔M=2048，自相关仿真结果如图2-28 所示。横轴表示时延，纵轴表示归一化幅度。从图2-28 看出，类似于δ 函数，接近白噪声的特性。

(www.xing528.com)

图2-28　Tent 的自相关

取序列长度N=1024，A=1/2，B=1.9999，z（0）=0.289999，y（0）=0.290000，最小初始值敏感度为10-6，相关间隔M=2048，互相关仿真结果如图2-29 所示。横轴表示时延，纵轴表示归一化幅度。由图2-29可以看出，互相关系数非常小，随着序列长度的增加会逐渐趋近于白噪声。而且，对于初始值相差10-6的两个序列经过数次迭代后，互相关性变得非常小。

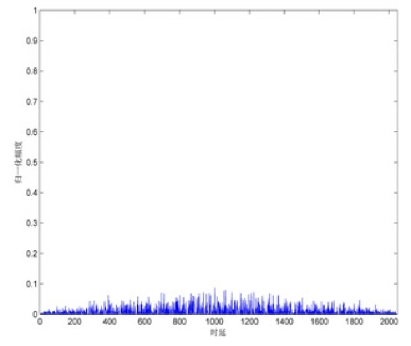
图2-29　Tent 的互相关

5. Tent 的倍周期分岔

当B 的取值范围是(0,2)时，Tent 映射是从区间(0,1]到其本身的非线性映射。B 以0.004 的步长，在(0,2)区间逐步增加时，对每一个固定的B 值，取一个初始值z（0）=0.289999，通过对式（2-20）进行500 次迭代运算，每当给定一个B 值后，取其最后500 次的z（n）值进行绘图，其结果为倍周期分岔图，如图2-30 所示。图2-30 中横坐标表示B 的取值范围，纵坐标表示z（n）的取值范围。

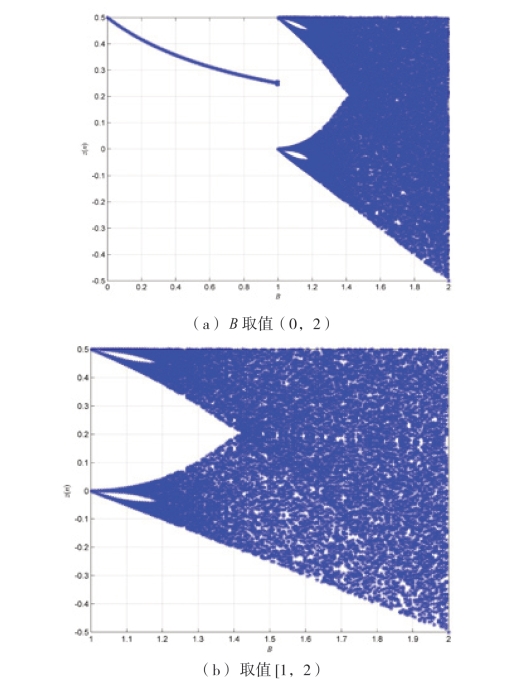
图2-30　Tent 的倍周期分岔

从图2-30 可以看出，当B 的取值范围是(0,2]时，Tent 映射取值逐渐增多。当B 的取值范围是(1.4,2）时，Tent 映射是从区间[-0.5,0.5]到其本身的非线性映射。

6. Tent 的Lyapunov 指数

式（2-20）Tent 的Lyapunov 指数的表达式：

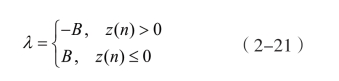
B 以0.001 的步长，在区间(0,2)逐步增加时，对每一个固定的B 值，取一个初始值z（0）=0.289999，n=200，得到李雅普诺夫指数图，如图2-31 所示。图中横坐标表示B 的取值范围，纵坐标表示Lyapunov 指数。

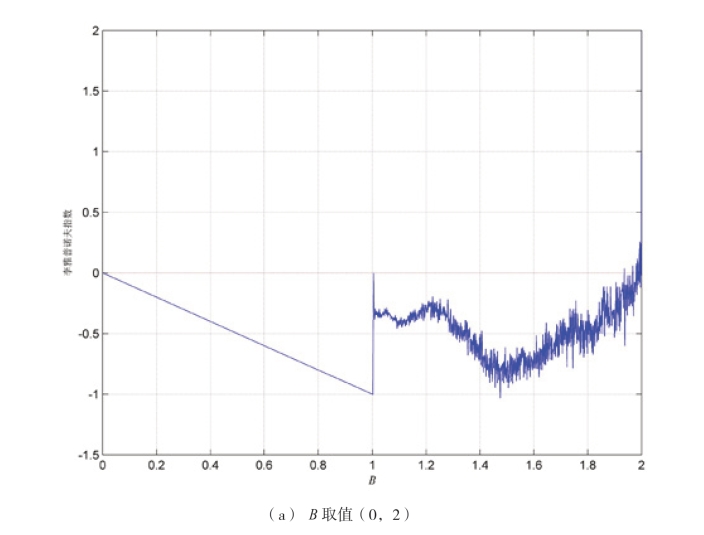
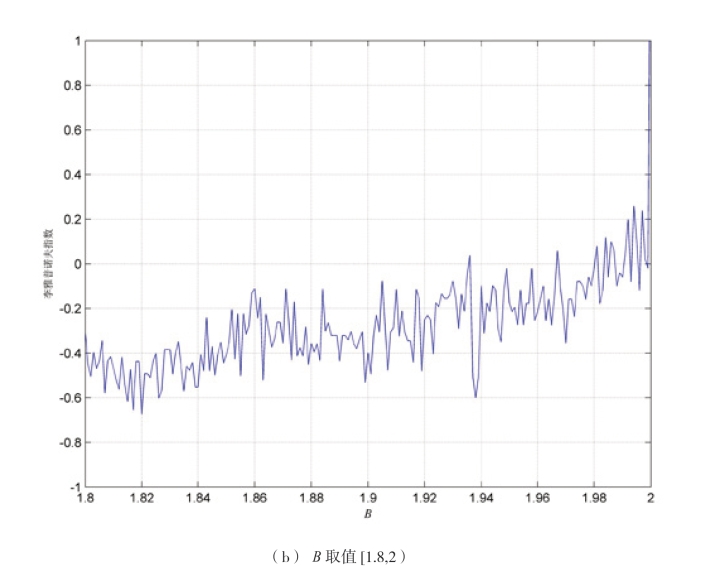
图2-31　Tent 的Lyapunov 指数

从图2-31（a）可以看出，当B ＞1.8 时具有正的Lyapunov 指数，该映射处于混沌状态。从图2-31（b）可以清楚地看出，B 在1.9 附近时Lyapunov指数为负，出现波动。当B=1.999，由式（2-20）迭代产生Tent 混沌序列，见图2-25 所示，由该映射产生的混沌序列z（n）在区间[-0.5,0.5]上遍历，该映射为满秩映射。