Lorenz方程特性与仿真应用

1. Lorenz 的初值敏感性

Lorenz 混沌系统具有初值敏感性的特征。系统参数a = 10, b = 8/3, c = 28 ，初始值为y（0）=z（0）=0.1，x（0）分别为0.1 和0.100001，对式（2-19）进行200 次迭代，就可以得出图2-17 所示Lorenz 混沌映射的初始值敏感图。横轴表示时间t，图2-17（a）纵轴表示序列的取值x（t），图2-17（b）纵轴表示序列的取值y（t），图2-17（c）纵轴表示序列的取值z（t）。从图2-17可以看出，刚开始迭代的两条曲线基本重合，但是经过一段时间的迭代后，两个曲线有很大的差别，只对x 的初值改变了10-6就导致Lorenz 系统的三组序列发生很大的变化，这说明了Lorenz 系统对初值非常敏感。

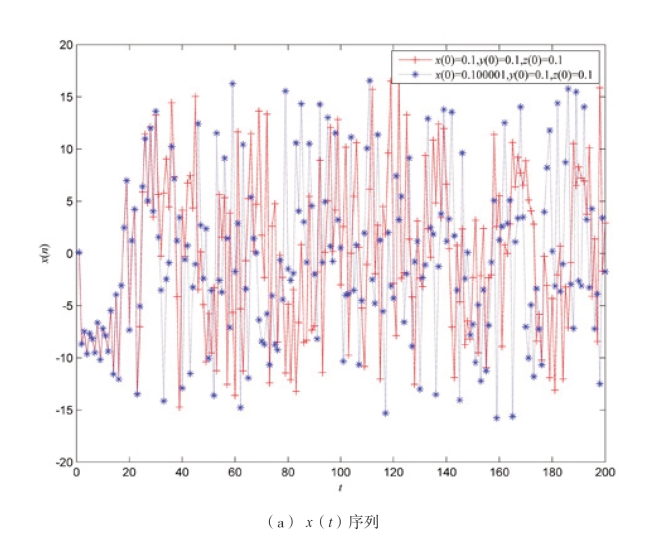
图2-17　Lorenz 的初始值敏感性

2. Lorenz 的遍历性

取初始值x（0）=y（0）=z（0）=0.1，系统参数a=10,b=8/3,c= 28，对式（2-19）进行1000 次迭代所产生的混沌轨迹如图2-18 所示。横轴表示时间t，图2-18（a）纵轴表示序列的取值x（t），图2-18（b）纵轴表示序列的取值y（t），图2-18（c）纵轴表示序列的取值z（t）。图中的“+”表示t 时刻运算值。从图2-18 中可以看出，当迭代次数足够大时，模拟混沌序列的取值x（t）几乎遍历了[-20,20]的区间，模拟混沌序列的取值y（t）几乎遍历了[-25,25]的区间，模拟混沌序列的取值z（t）几乎遍历了[0,45]的区间。

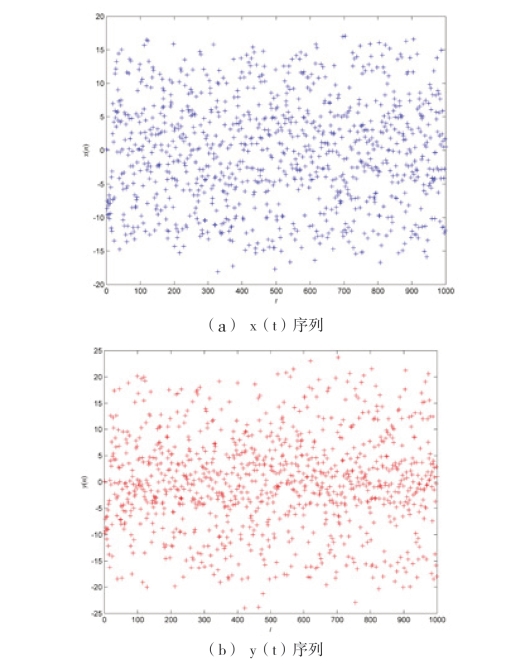
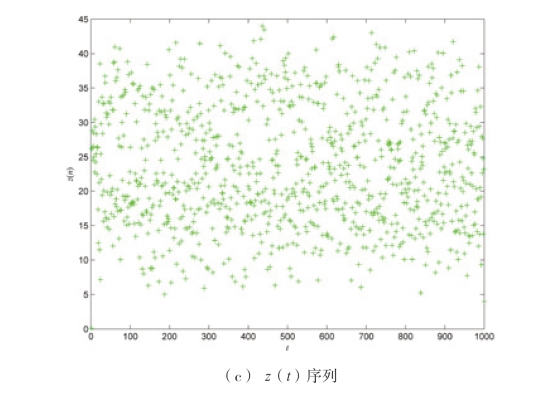
图2-18　Lorenz 的遍历性

3. Lorenz 的相空间

Lorenz 混沌序列在二维空间上的投影像一个横写着的“8”。取初始值x（0）=y（0）=z（0）=0.1，系统参数a=10,b=8/3,c= 28，得到图2-19（a）Lorenz 系统在x-z 上的投影，图2-19（b）Lorenz 系统在y-z 上的投影，图2-19（c）Lorenz 系统在x-y 上的投影，图2-19（d）为Lorenz 系统的三维相空间。

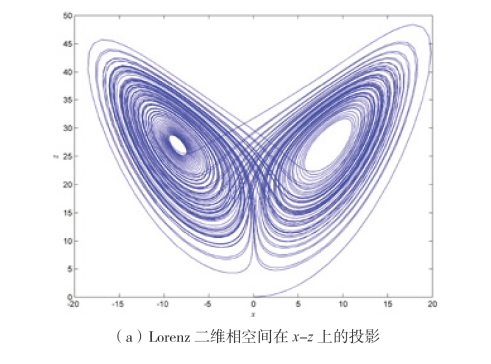
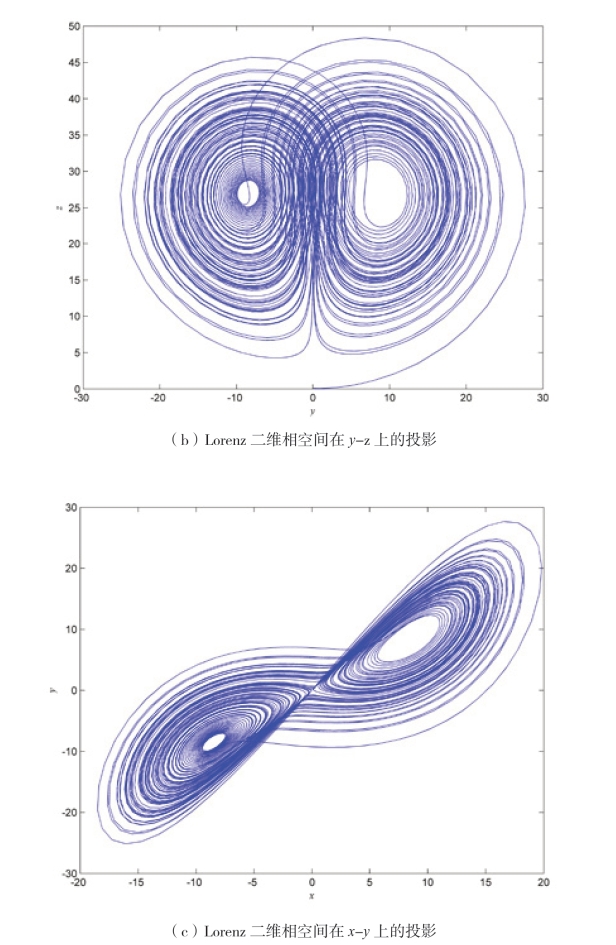
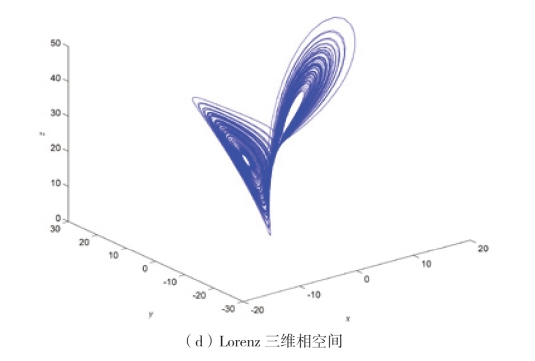
图2-19　Lorenz 的相空间

4.Lorenz 的相关性(https://www.xing528.com)

取序列长度N=1024，系统参数a=10,b=8/3,c= 28，初始值x（0）=y（0）=z（0）=0.1，相关间隔M=2048，自相关仿真结果如图2-20 所示。从图2-20可以看出，x（t）或y（t）的自相关类似于δ 函数，接近白噪声的特性，z（t）的自相关性差，因此Lorenz 常常选取x（t）或y（t）序列。

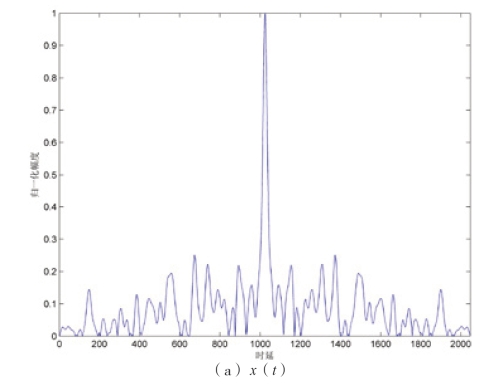
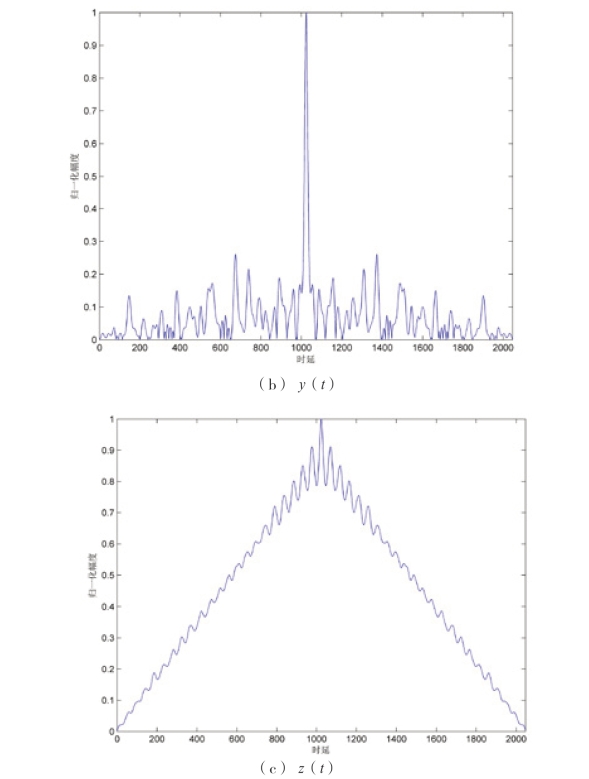
图2-20　Lorenz 的自相关

取序列长度N=1024，系统参数a=10,b=8/3,c= 28，初始值x（0）=y（0）=z（0）=0.1，另一组初始值x（0）=0.100001，y（0）=z（0）=0.1，x 最小初始值敏感度为10-6，相关间隔M=2048，互相关仿真结果如图2-21 所示。由图2-21 可以看出，x（t）或y（t）的互相关系数非常小，随着序列长度的增加会逐渐趋近于白噪声。而且，对于初始值相差10-6的两个序列经过数次迭代后，互相关性变得非常小。z（t）的互相关性差，因此Lorenz 常常选取x（t）或y（t）序列。

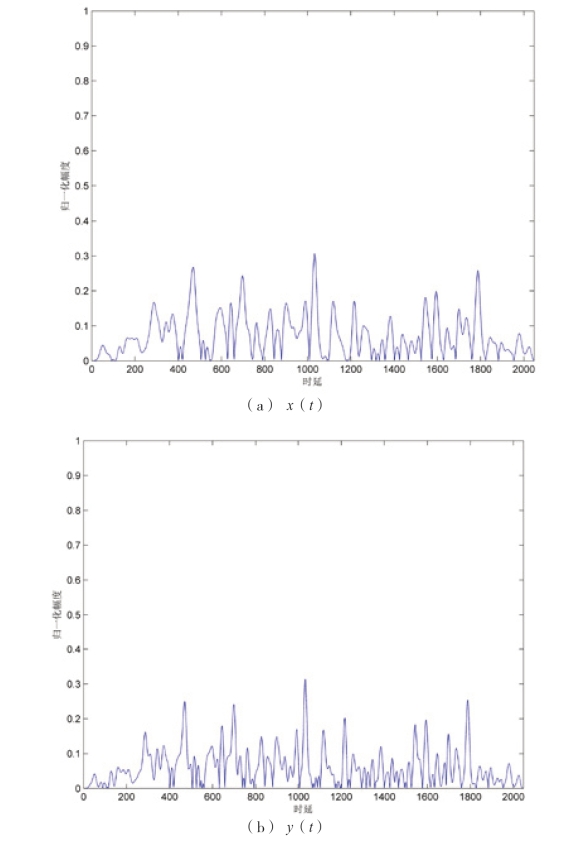
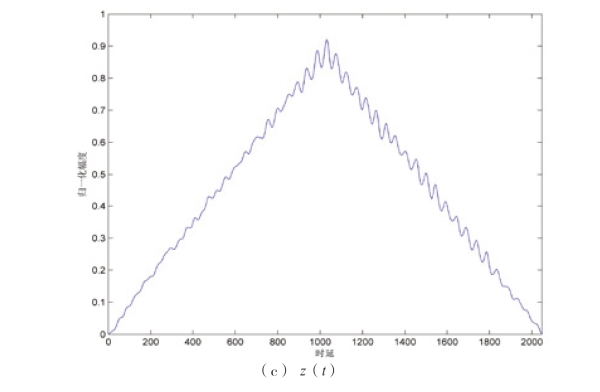
图2-21　Lorenz 的互相关

5.Lorenz 的倍周期分岔

系统初始值x（0）=y（0）=z（0）=0.1，系统参数a=10，b=8/3，c 的取值范围（0，50）由倍周期分岔图，如图2-22 所示，可知在c=24.74 时Lorenz 系统已经完全进入混沌状态。

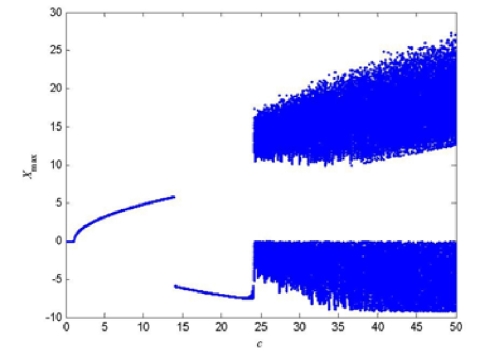
图2-22　Lorenz 的倍周期分岔

6.Lorenz 的Lyapunov 指数

李雅普诺夫指数是衡量一个系统进入混沌状态的重要指数。Lyapunov 指数是定量描述相空间中相邻轨道随时间变化按指数规律吸引或分离程度的物理量。

在一维映射中只有一个λ 值，而在三维相空间情况下一般就有三个λ，而且沿着相空间的不同方向，λ 值一般也不同。