广义裂纹生长问题练习：轻量化设计计算与构件结构

练习图33-1所示为安装在一个桁梁中的拉弦杆。弦杆承受正弦波形的脉动应力载荷Δσ∞=100N/mm²。在弦杆上产生了一个长度为a₀=10mm的裂纹。计算该弦杆到断裂前，还能承受的载荷交变次数为多少？

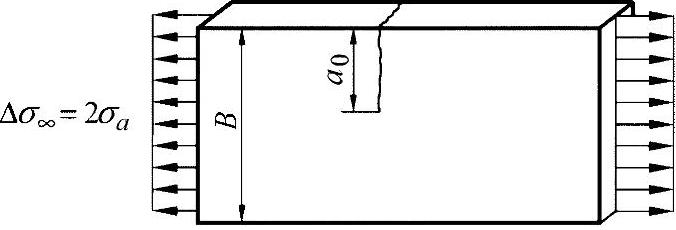
练习图33-1 拉弦杆

材料参数：m_p=2.7

C_p=2.54×10^-11（对于MPa m，m）

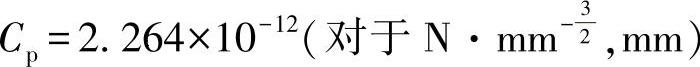
B=70mm

t=4mm

K_IC=4000Nmm^-3/2

根据24.8节中的结构，该问题可以用Paris方程求解，计算如下：

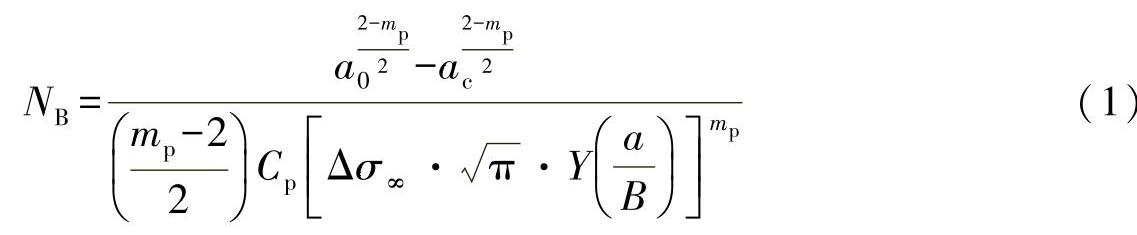
修正因子为

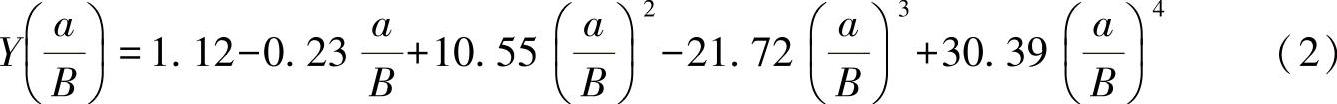
在公式中，临界裂纹长度a_c为未知的。参照方程式（24.32），该长度可以由周期应力强度的超出计算得出：

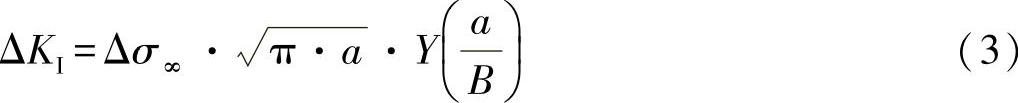
为此须满足，将最大裂纹长度进行周期分割，并且对于假设的裂纹长度确定修正函数和应力强度。在应力强度下，超出断裂韧性（K_Ic）的裂纹长度，可以被看做是临界裂纹长度。在本节中，可假设临界裂纹长度为a_c=40mm。(www.xing528.com)

如练习图33-2所示，经过以上计算，方程式（1）依然无法直接求解，因为该方程式由一个积分给出[见方程式（24.37）]，因此须考虑到与裂纹长度相关的修正因子。这里须选择一个迭代解法。

练习图33-2 临界裂纹长度的计算

要计算的方程为

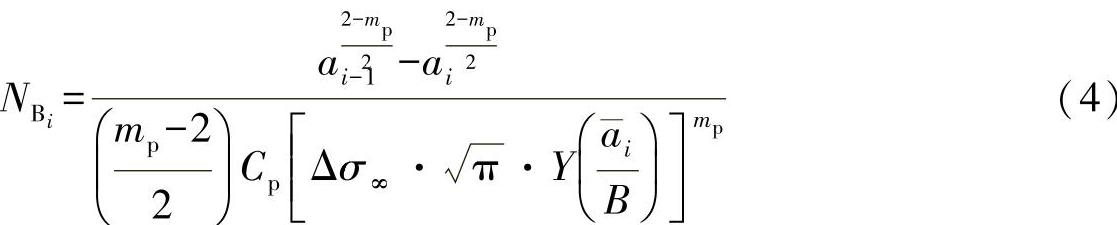
通过周期性叠加，可以得出直至断裂的总载荷交变为

为了对方程式（4）进行评估，如下选择了一个表格。其原则为

●在直至a_c的任意截面上的裂纹路径分割（从10到15，从15到20）；

●在间隔的中心上确定裂纹修正函数；

●将该波纹代入方程式（4）；

●将初始裂纹从10mm向前驱动到15mm，可得出所要求的应力循环次数。

通过在裂纹变化过程中进行叠加可以推断出，拉弦杆从产生初始裂纹开始直至断裂，可再承受N_B=54425LW次交变载荷。