轻量化设计：板材域与管的凸起练习

练习图26-1所示为一正交各向异性矩形盘，承受轴向压载荷。下面对盘的凸起进行研究。需要考察的是，各端支座的影响有多大；平板什么时候可以作为板杆来计算，什么时候可以作为板条来计算。

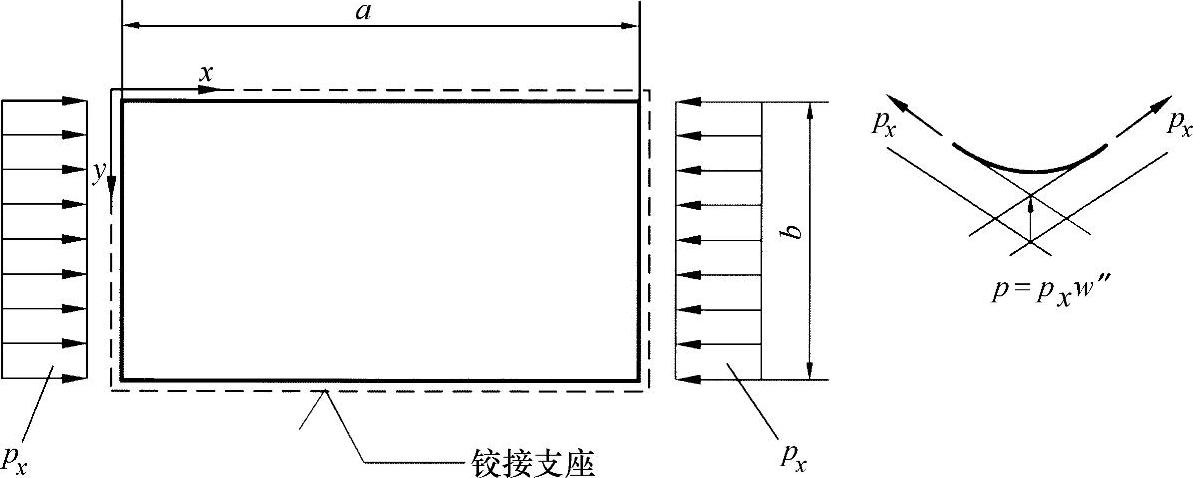
练习图26-1 矩形盘

按照方程式（19.1）有如下关系：

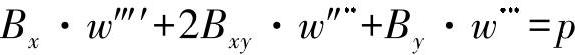
在该方程中，外载荷p与中心平面平行。由于在研究不稳定问题时，通常都是从变形的结构出发，因此现在必须要考虑由于中心平面翘曲而产生的反作用力。对于上面的凸起问题，可计算如下：

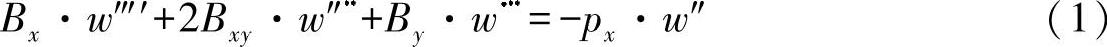
当出现极限载荷p_x=p_x边界时，凸起正好发生在中心平面上。

对于中心平面的挠曲，可进一步得出已知的双列表达式[见方程式（19.8）]：

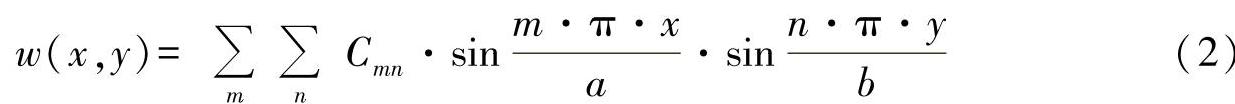
式中，m、n为半波数目。

通常对该方程进行求导，并代入方程式（1），则可生成以下的特征方程：

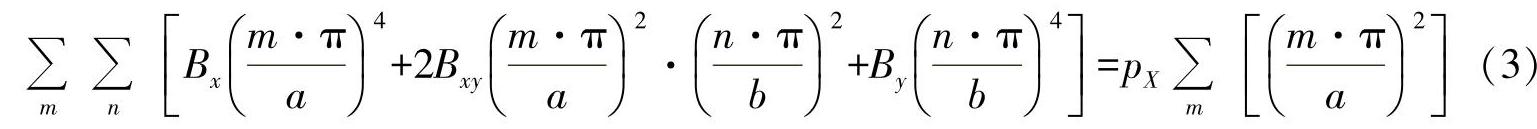
或者转换为

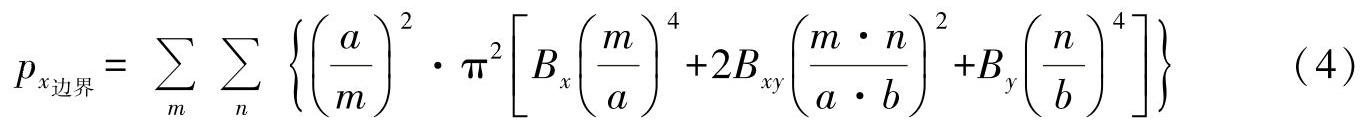
这里引入了如下参数：

●抗弯刚度，，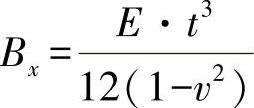

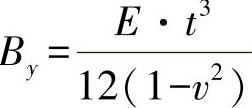
●对角刚度，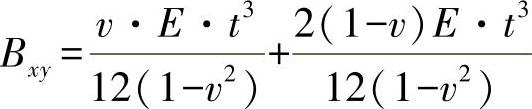

现在对方程式（4）进行转换，则无尺度的凸起数k得以分离出来：

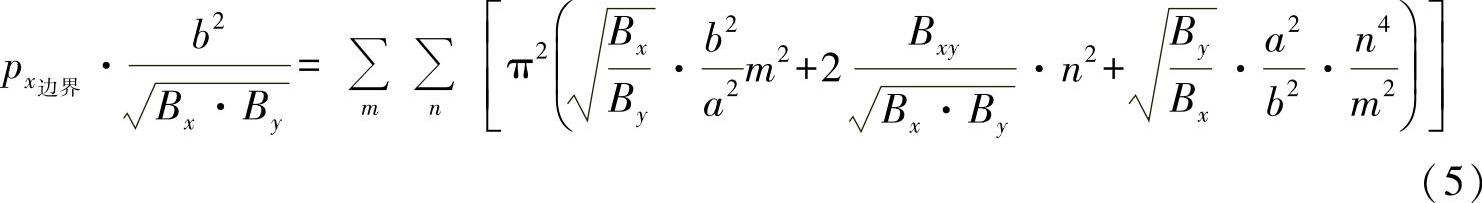
对于临界轴向压力，则有下述关系：

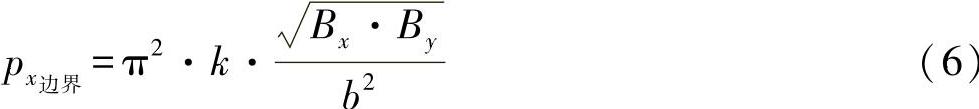
由方程式（5）可进一步求解出下列参数值：

●对角数

●有效的长宽比

●长宽比的倒数

由此，可求得凸起数为(www.xing528.com)

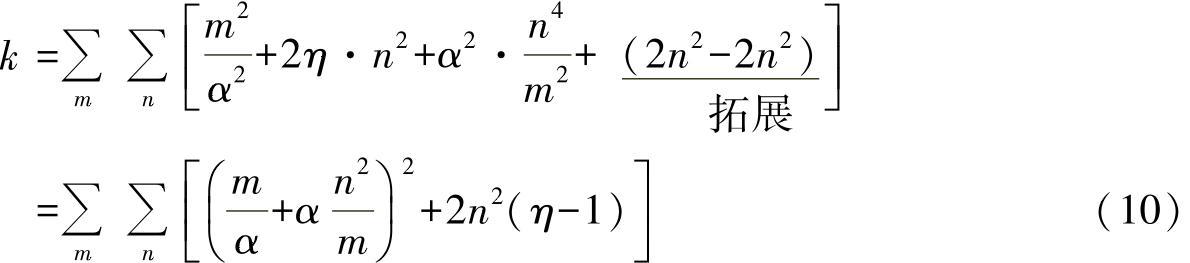
考虑到只有载荷p_x作用，所以在y方向上的凸起没有意义，因此可设置n=1（在y方向上波纹数）：

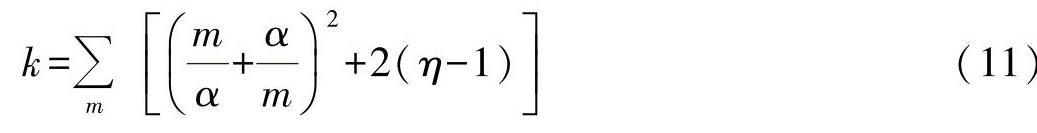
现在用值k-2（η-1）作为参数来描述长宽比α，则可以得到如练习图26-2所示的曲线变化。

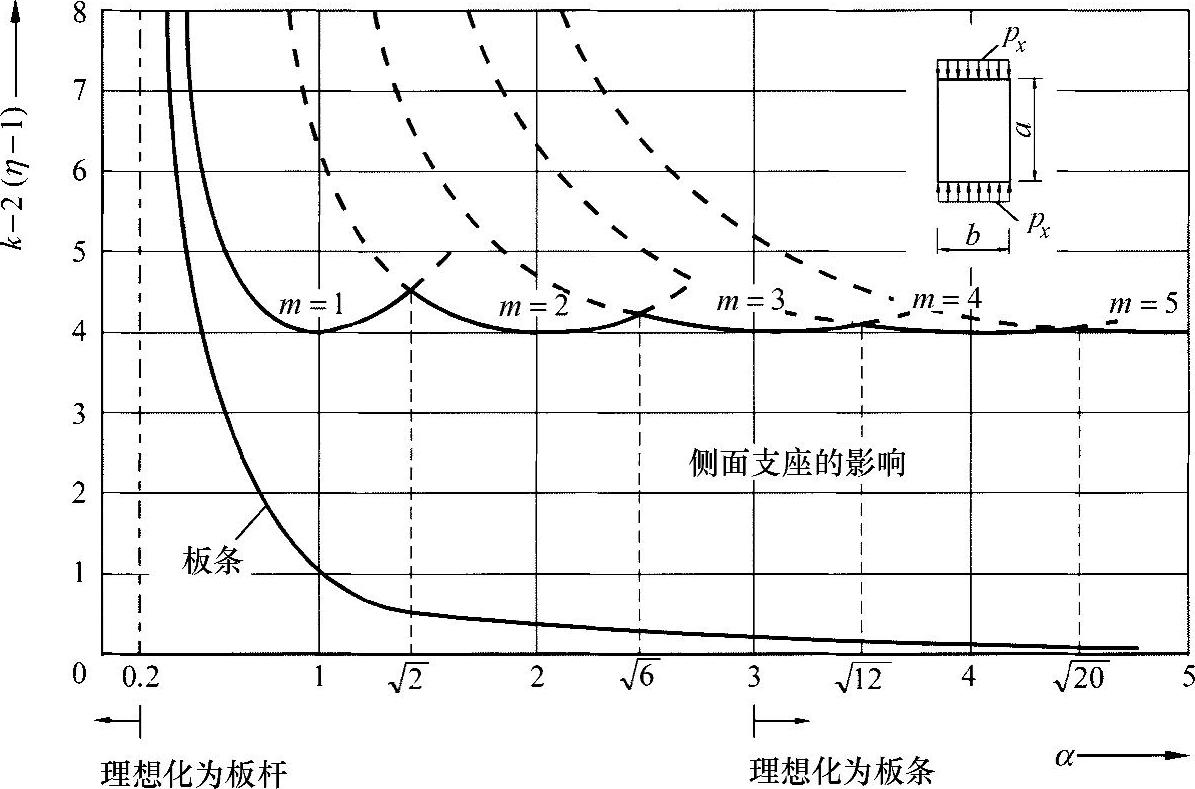
练习图26-2 凸起函数的变化过程

曲线具有相同的最小值，可通过下面的求导得出，对于所有波纹数m有：

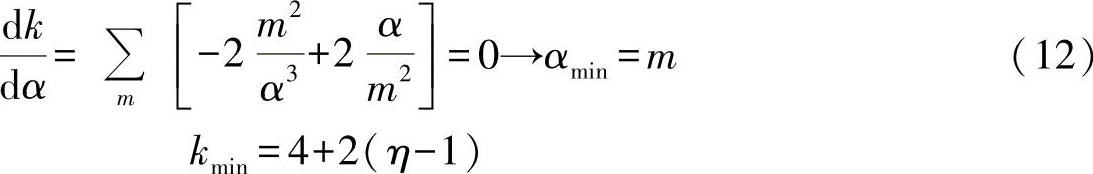
或者

k_min-2（η-1）=4 （13）

由于总是将凸起值设置为最小值，所以极限曲线就表现为吊挂曲线变化过程。曲线的截点为

k_m=k_m+1

或者

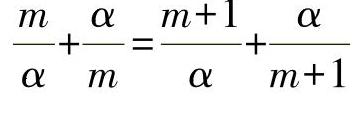
即

另外，还需要考虑到凸起问题的下述边界情形：

●如练习图26-3所示，将板杆模拟为在两个支座上的横梁：

以在y方向上的伸展无关紧要作为前提条件，则方程式（4）可转换如下：

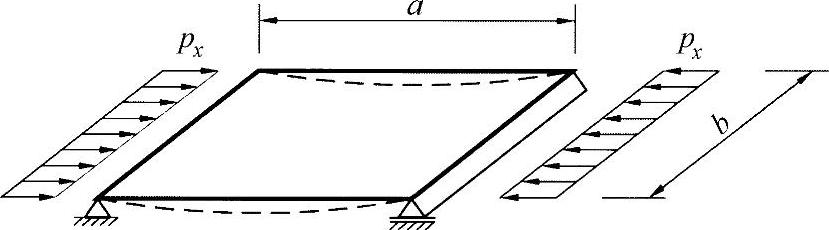
练习图26-3 板杆

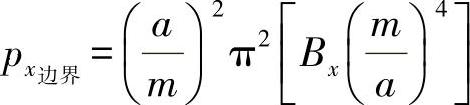
或者对于m=1，有：

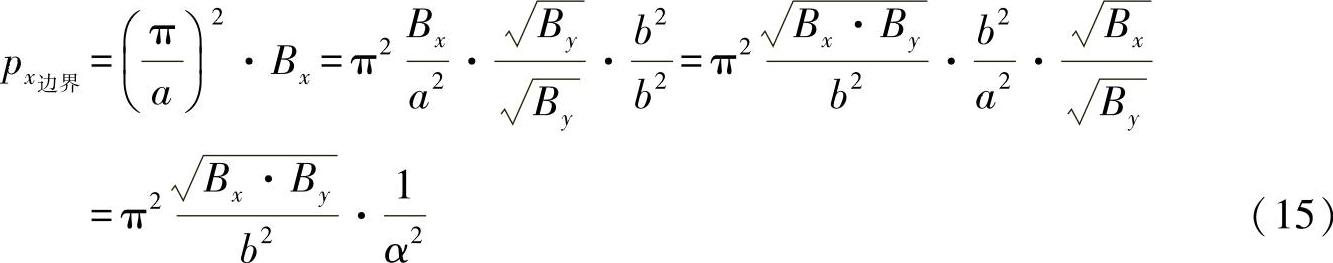
由此得出的曲线变化可见上面练习图26-2所示。当比例α<0.2时，曲线调整幅度很大，以至于所有端铰接支承的平板都可以简化为板杆。

●板条

从上面的吊挂曲线可以看出，对于有效长宽比α→∞，凸起值k→4。根据图表中的边界，这意味着，端面支承与端支承相比，其影响可近似忽略不计。当α=3，所有端铰接支承的平板都可以较小的误差简化为板条，如练习图26-4所示。

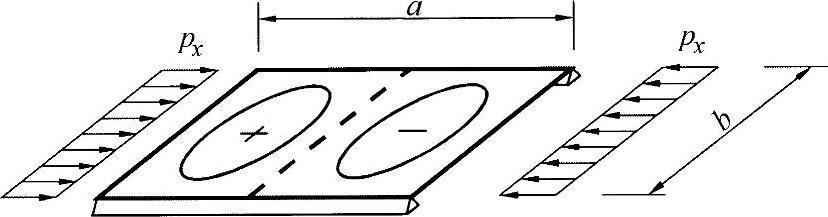
练习图26-4 板条