轻量化设计：不对称型材压弯的实践

练习图25-1所示为一个长度为L的两端铰接支承的压杆，其横截面不对称，欲求解弯曲扭转压弯的临界载荷。杆在中心处受压，终端横截面在位移的作用下保持在平面内，并且不承受弯曲应力。

对于型材，已知有：

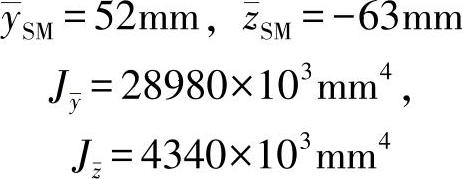
J_t=130×10³mm⁴

C_W=0（对于无翘曲支座）

A=3900mm2

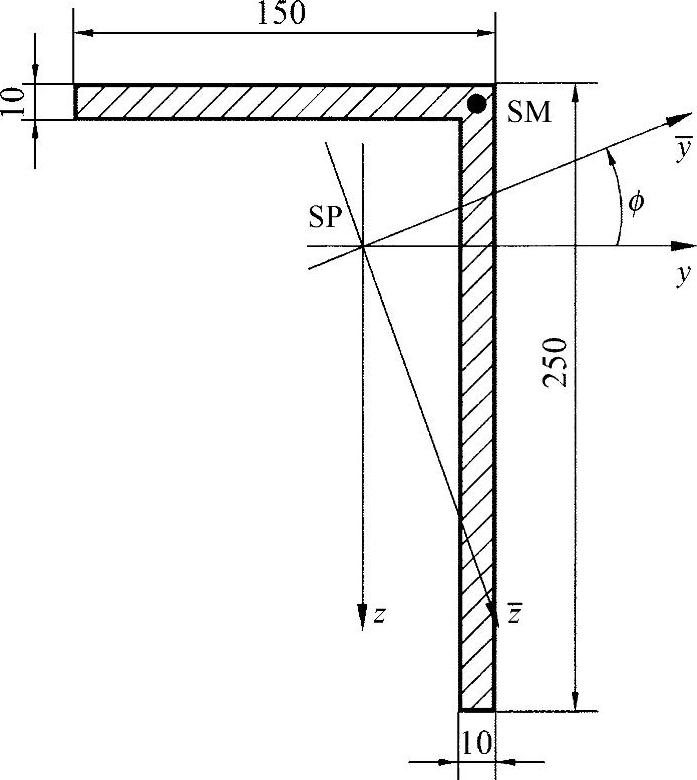
练习图25-1 不对称角型材

对于这里产生的弯曲扭转压弯，在方程式（18.26）中给出不稳定条件：

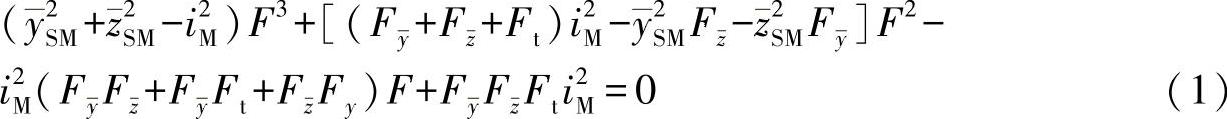
式中 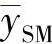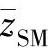，——剪切中心的坐标；

i_M——基于剪切中心的惯性半径，

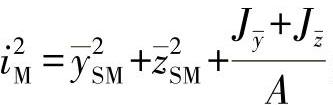； (2)

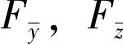——根据欧拉公式，由弯曲在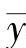轴与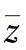轴上的产生临界压弯载荷，

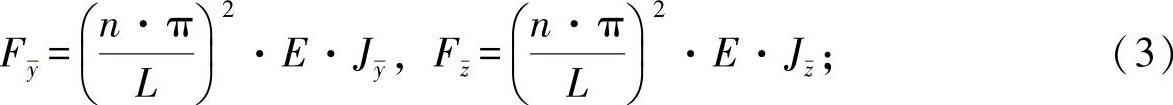
F_t——由围绕纵向轴x的扭转产生的临界压弯载荷，

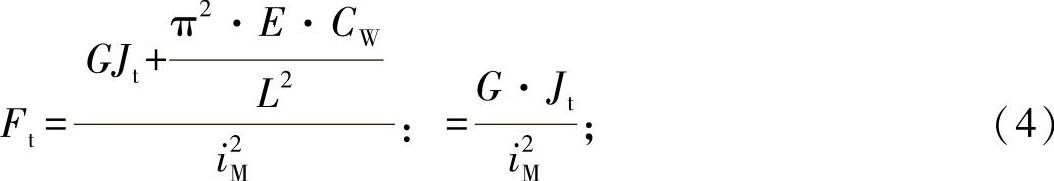
μ——弯曲线的特征值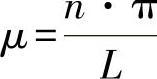，。 (5)

对于上面的例子，应首先将方程式（2）～（5）代入方程式（1），由此可得出：

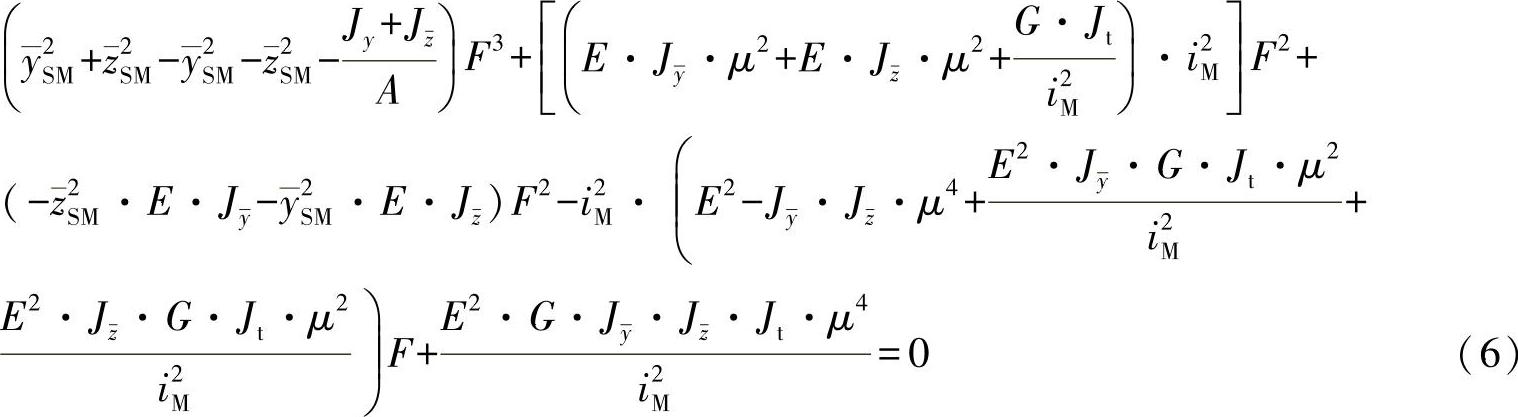
或者(www.xing528.com)

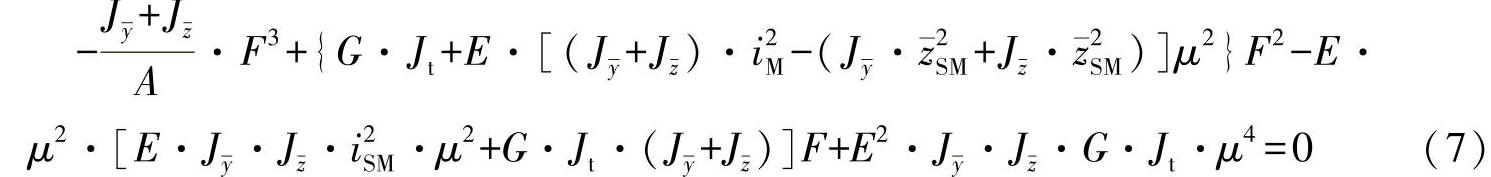
系数包括了几何形状的横截面值，材料值E和G，以及杆长度的特征值_μ与在弯曲中产生的正弦波纹数目。

如果进一步通过

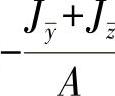分解，并且代入与问题相关的值，则可以得出：

i²_M=15.22×10³mm² （8）

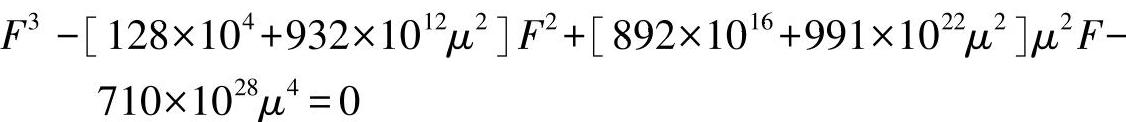
由该方程可以得出作为函数μ的临界载荷F_临界，当n=1时，为最小的真实根。

现在，可以针对不同的长度关系计算出临界载荷：

F³-369×10⁶·F²+5.06×10¹²·F-1.11×10¹⁸=0

F_临界=301kN

单独按照欧拉公式研究压弯，对于所考察的长度，根据方程式（3）可得出临界载荷如下：

L=1000：F_临界=9000kN

L=2000：F_临界=2250kN

L=3000：F_临界=1000kN

L=4000：F_临界=560kN

L=5000：F_临界=360kN

如练习图25-2所示，这一结果在下面以图表的形式表示出来。可以看出，在短杆的情况下，按照欧拉公式（弯曲压弯）得出的临界载荷与弯曲扭转压弯的临界载荷之间差异很大。对于较长的杆来说，其差异则很小。

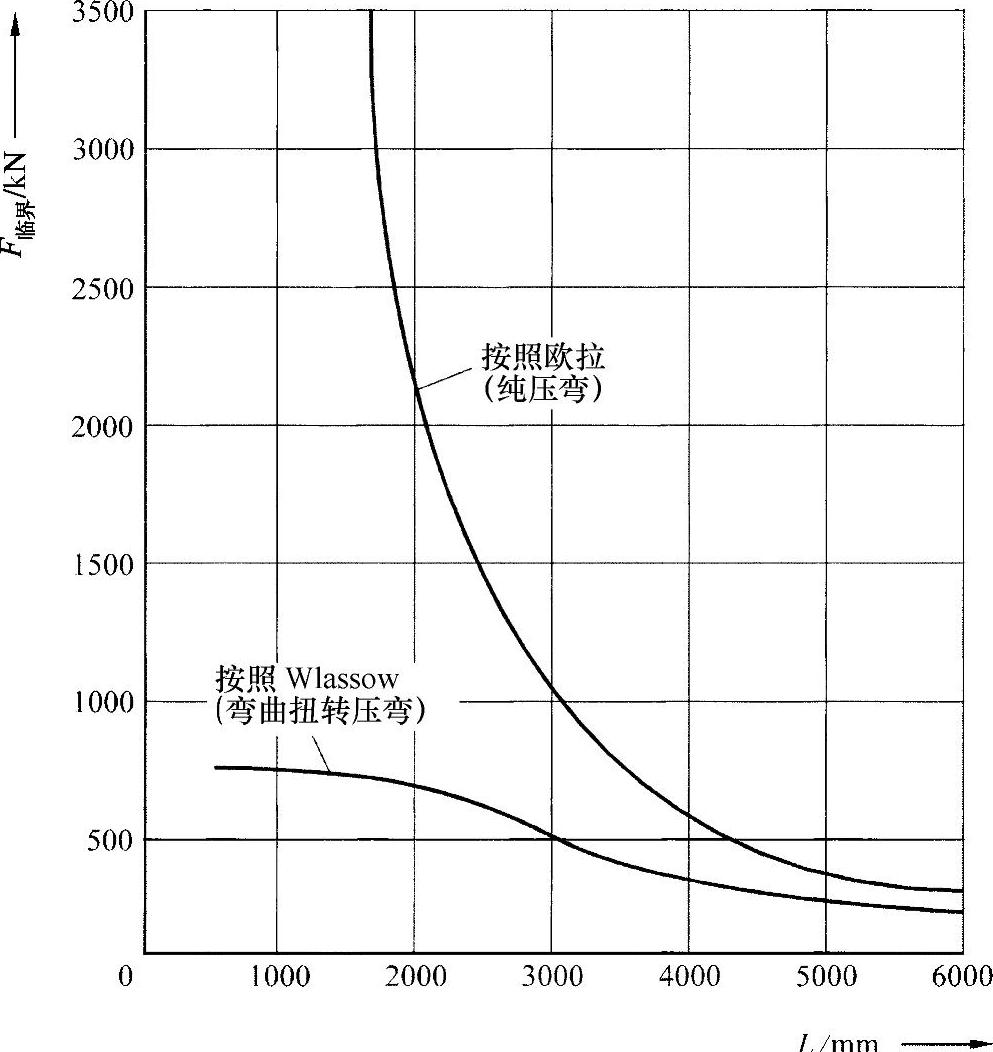
练习图25-2 在压弯长度上临界载荷的变化过程