【摘要】:在18.2.1小节中考察了一个杆,压载荷正好作用在这个杆的面积重心上。练习图24-1中所示的杆在x-z平面是对称的,承受偏心的压力作用,由载荷F导致的最大挠曲w和最大法向应力可如下计算。已知:Jy=J、Wy、A、L根据自由体图,可确定内弯曲力矩为M=F(e+W) 练习图24-1 偏心压杆根据方程式有:M=-E·J·w″ 将方程式代入方程式,并且通过微分方程转换有:借助下述方程:可按照方程式列出广义形式为w″+μ2w=C5+C6·x 其中,C6=0,C5=-μ2·e。
在18.2.1小节中考察了一个杆,压载荷正好作用在这个杆的面积重心上。实际中很少会遇到这样的情形,一般总是会存在轻微的直线度误差和偏心度,其结果就是,真实的杆不会按照抗冲击设计方向发生弯曲,而是先发生压弯,然后由于产生了不允许的应力导致失效。
练习图24-1中所示的杆在x-z平面是对称的,承受偏心的压力作用,由载荷F导致的最大挠曲w(x)和最大法向应力可如下计算。
已知:Jy=J、Wy、A、L
根据自由体图,可确定内弯曲力矩为
M=F(e+W) (1)
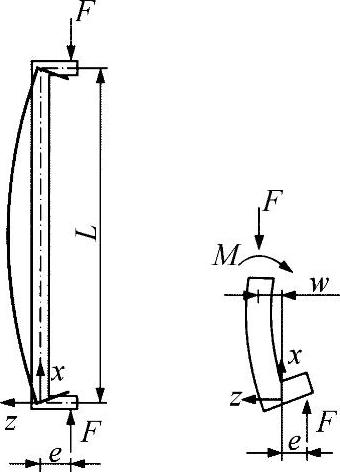
练习图24-1 偏心压杆
根据方程式(18.7)有:
M=-E·J·w″ (2)
将方程式(2)代入方程式(1),并且通过微分方程转换有:

借助下述方程:

可按照方程式(18.11)列出广义形式为
w″+μ2w=C5+C6·x (5)
其中,C6=0,C5=-μ2·e。 (6)
适合于方程式(5)的解式为
w(x)=C1·cosμ·x+C2·sinμ·x-e (7)(https://www.xing528.com)
由边界条件w(0)=0,可得出C1=e。由边界条件w(L)=0,可得出方程式:

还有

与
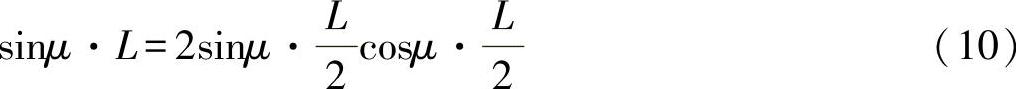
由方程式(9)和(10)可以得出:

将常量代入方程式(7)后,可用以下方程来描述弯曲线:
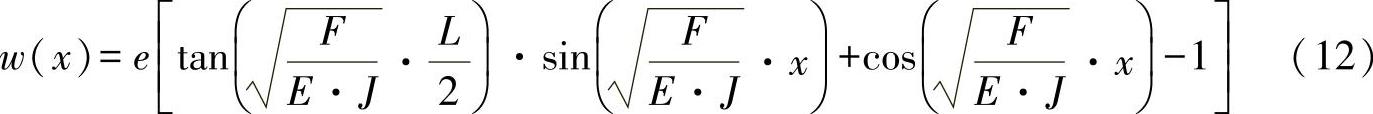
最大挠曲为
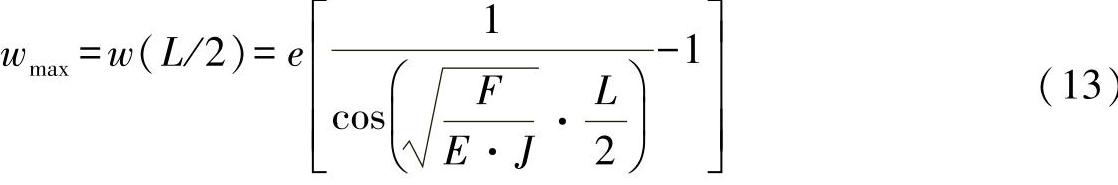
由弯曲应力与法向应力的叠加可得出应力为

利用方程式(1),可求出最大应力为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




