如练习图22-1所示的压杆带有弹性中间支座,须确定与弹簧刚度相关的临界压力。
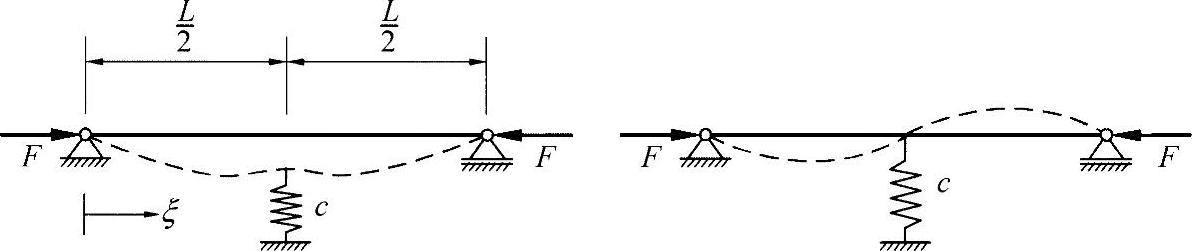
练习图22-1 压杆的对称压弯与反对称压弯形式
在压杆失效的情形下,可根据中间支座的刚度情况,假设压杆的压弯形式为对称的或者反对称的。
在反对称压弯形式下,中间支座上没有产生载荷。因此,临界压力对应于长度为LK=L/2的两端铰接叠加杆的欧拉压弯载荷为
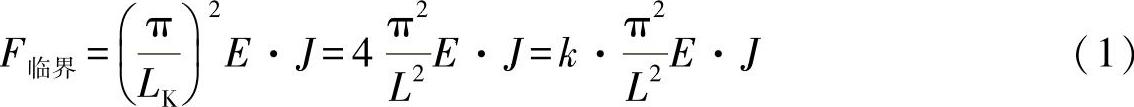
这里,用k=4求解问题的凸起值。
在对称的形式下,须求解微分方程[也可参见方程式(18.8)]:

其中,
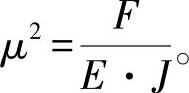
对应的解法表达式为
w(ζ)=C1+C2·ζ+C3·cosμ·ζ+C4·sinμ·ζ (3)
在位置0≤ζ≤2处,又可以得出积分常数为
w(0)=0:C1+C3=0 (4)
w″(0)=0:C3=0→C1=0 (5)
w′(ξ=1)=0:C1+μ·C4·cosμ=0 (6)
方程式(6)中,对应于两个未知量,只有一个方程式。如练习图22-2所示,通过释放弹簧,可以得到另外一个关系式,即:
2Q(1)=c·w(1) (7)
考虑到在梁弯曲情形下,还有:
M′=Q→Q=E·J·w(x)‴
则可以适当地推导出方程式(7)。
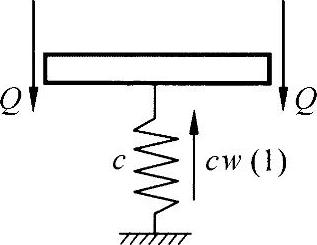
练习图22-2 在弹簧 上的力平衡(https://www.xing528.com)
这首先要求有一个方程的插入微分,即:
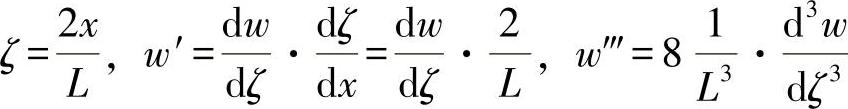
考虑到一半的桁梁长度,对方程式(7)可有:
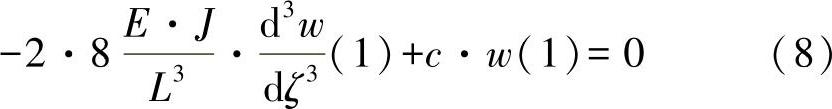
将其进一步代入方程,有:
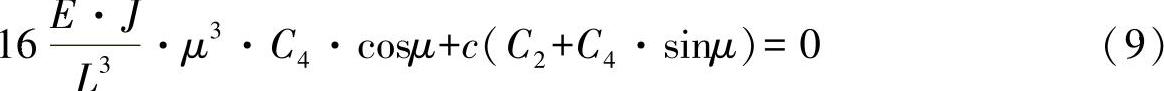
现在,对于依然未知的积分常量,通过方程式(6)和(9)可以生成一个方程组:
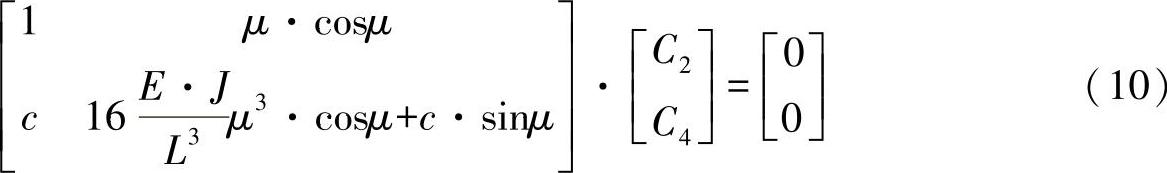
在消除系数行列式的要求下,可得出特征值方程为
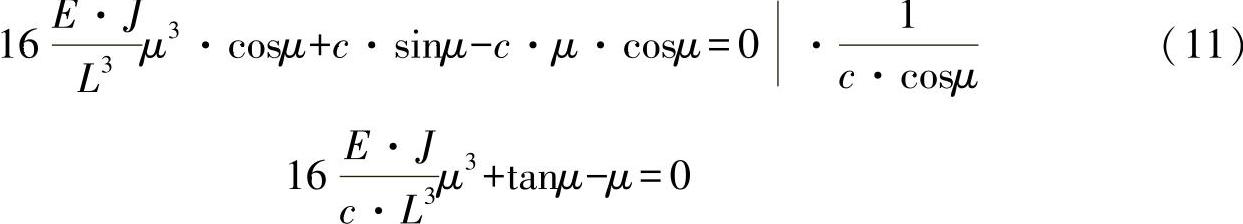
或
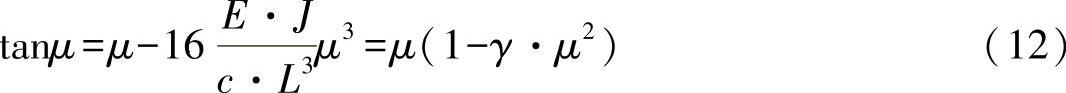
其中,可引入刚度参数:

在练习图22-3中,描述了将刚度参数作为特征值μ的函数的变化过程。
图中显示,当μ=π时,有最小特征值。这里,刚度参数为

在这个值的基础上提高刚度参数,并不能增加承载能力,因为杆会发生反对称压弯。由方程式(13)和方程式(14)可以得出刚度的极限值为
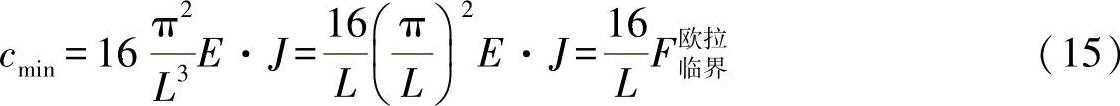
对以上计算进行归纳总结可以确定,通过一个支座可将承受的压弯载荷最大增加到欧拉压弯载荷的四倍;之后,再提高支座刚度,也只是能得到另外一种压弯形式而已。
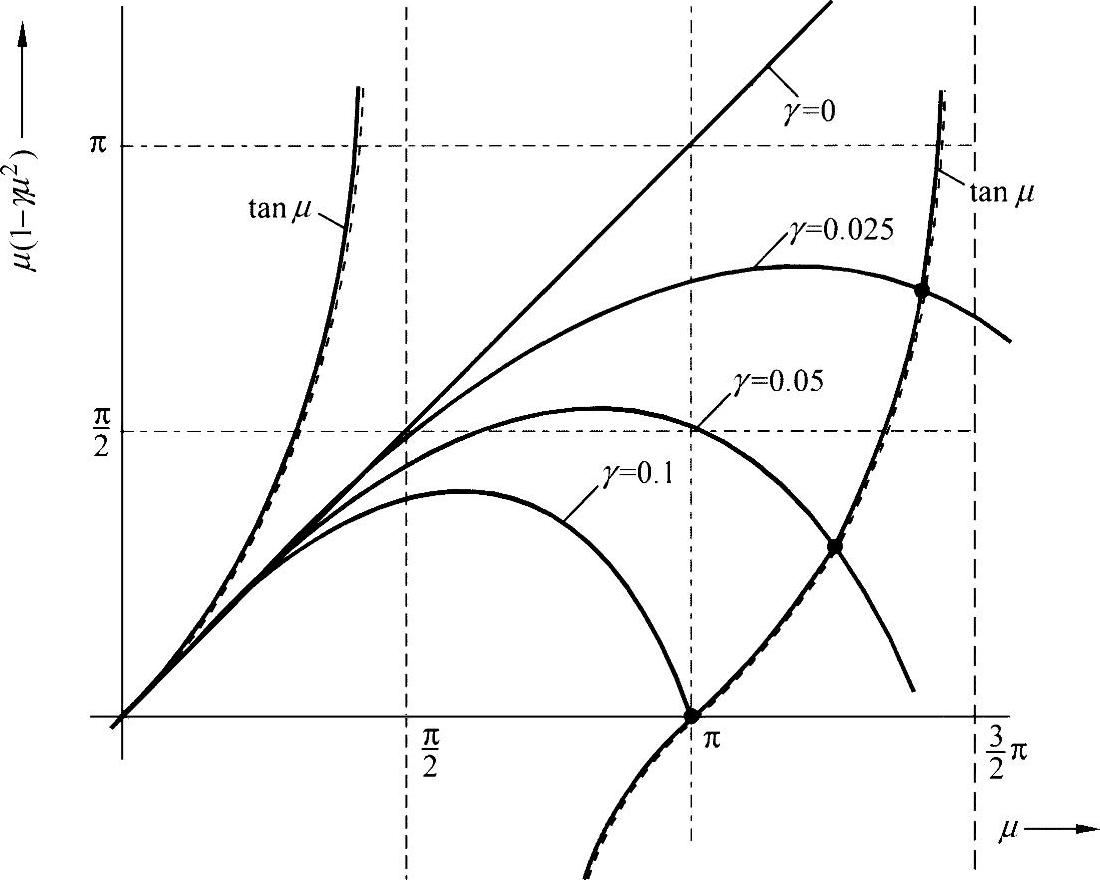
练习图22-3 特征值的表述
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




