三明治构件轻量化设计的计算基础与结构

练习图21-1中所示为一个两端铰接支座的三明治梁，承受分布载荷，须求出梁的最大挠曲。

考虑到剪切变形，可得出弯曲线的倾斜w（x）′：

w（x）′=γ（x）-β（x） （1）

描述横截面倾斜的旋转角β（x）可由下式求出：

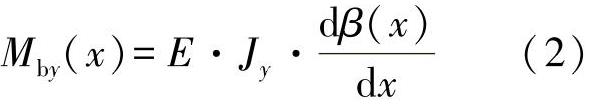
导致剪切变形γ（x）的内力大小为

Q（x）=G·A_s·γ（x） （3）

其中，A_s=b·h是三明治梁的横截面面积。对于上面给出的两端铰接支承的三明治梁，其内力变量变化为

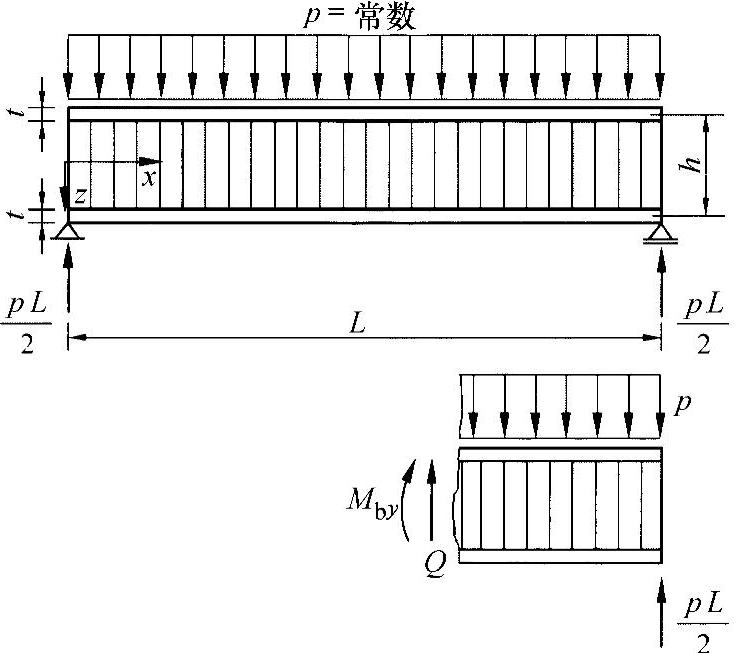
练习图21-1 宽度为b的三明治梁

由方程式（2）和（5）可得出旋转角的导数为

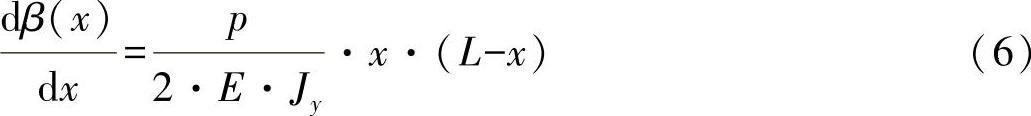
对方程式（6）进行一次积分，有：

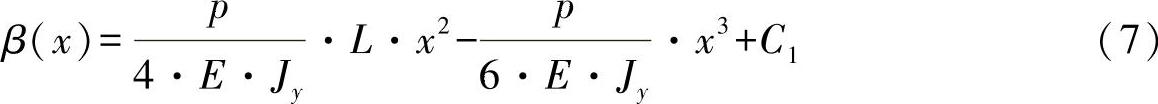
由方程式（3）和（4）求得剪切角γ（x）为

由此可以求出方程式（1）右边的两个参数，从而得出弯曲线的倾斜线为

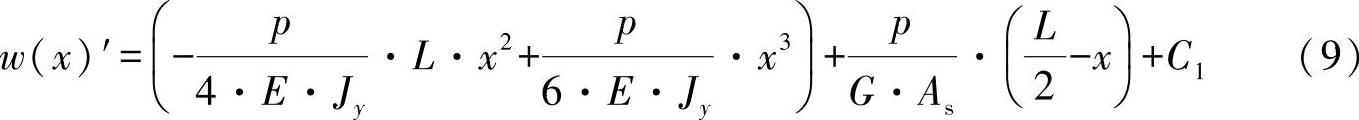
对上面的方程式进行积分，有：

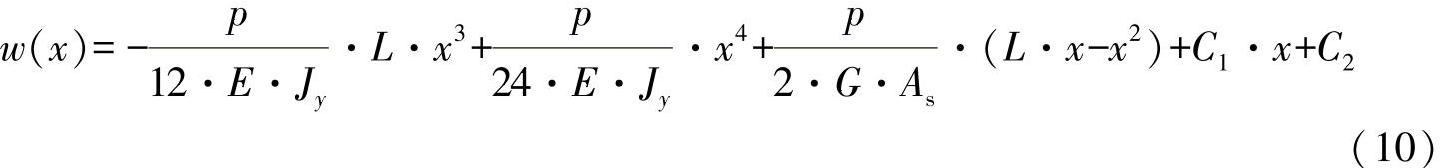
根据边界条件：

w（x=0）=0与w（x=L）=0（11）

可求出在方程式（10）中的两个常数：(www.xing528.com)

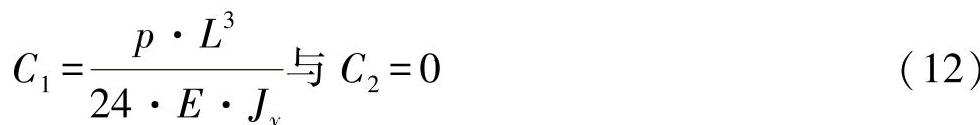
其中，对于弯曲变形，考虑到剪切影响，有以下方程式：

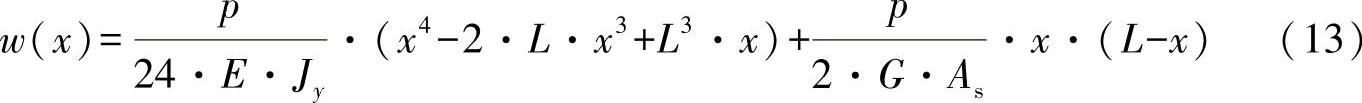
可以看出，根据部分挠曲理论，弯曲线方程式（13）由两部分组成，一个为纯弯曲分量：

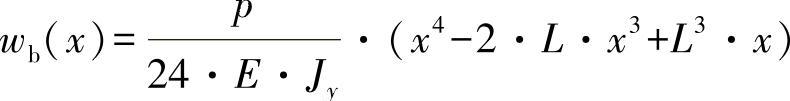
另一个为纯剪切分量：

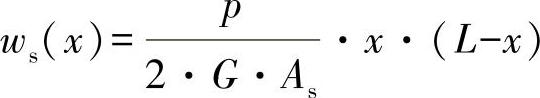
桁梁中心的最大总挠曲为

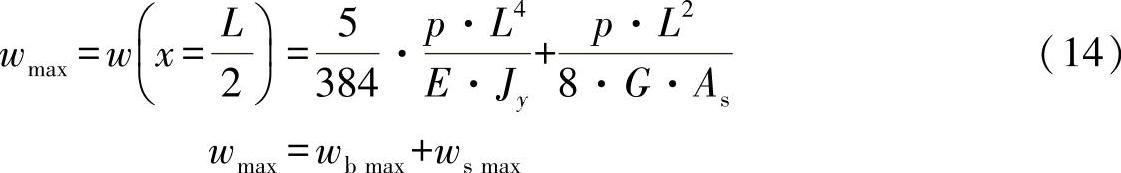
最大剪切分量与最大弯曲分量的比例关系为

从本质上来说，抗弯刚度E·J_y取决于上面板与下面板；其近似对应于用表皮平板E_H的弹性模量乘以Steiner分量：

E·J_y≈E_H·t·b·h^2[1] （16）

剪切刚度G·A_s则由形芯确定：

G·A_s=G_K·b·h （17）

考虑到方程式（16）和（17），有：

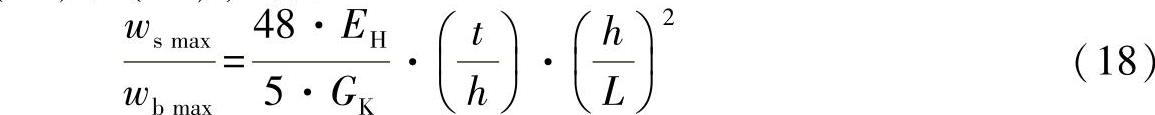
示例：铝表层和铝蜂窝芯

E_Al≈70000N/mm²，G_K≈100N/mm²，t/h=0.1

表中的结果表明，在短桁梁中，不允许忽略剪切力流。在长桁梁中，弯曲的影响则是主要的。练习图21-2所示为由方程式（18）得出的结果。

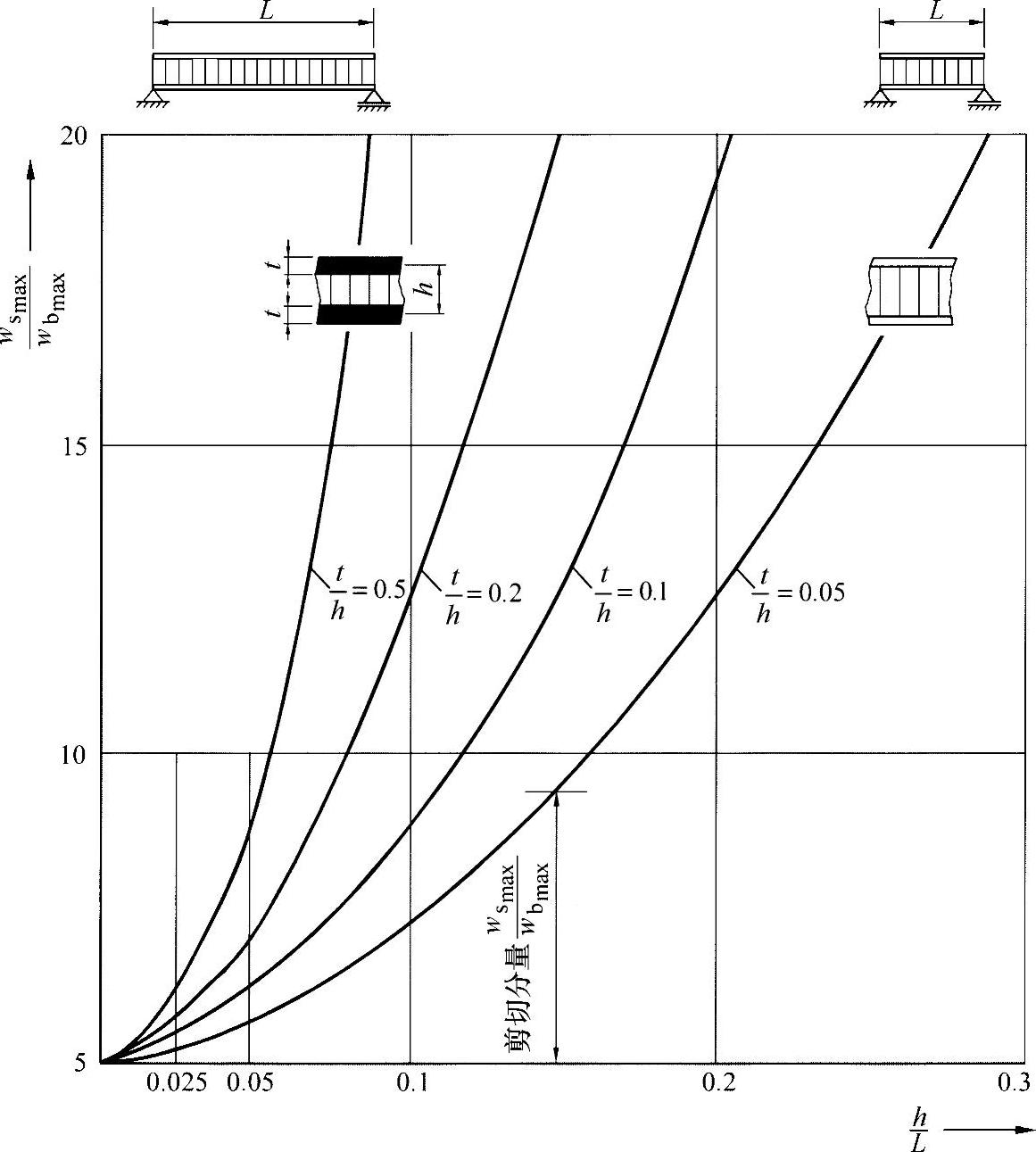
练习图21-2 三明治梁弯曲下剪切的影响，与梁的尺寸相关