【摘要】：如练习图18-1所示的框架承受分布载荷。对此，须通过做功原理以及由此得出的如下关系来确定变形：其中，i为力“1”的位置；k为实际载荷的位置。这里要特别注意的是，应采用合适的坐标系来进行计算。练习图18-1 框架与力矩面积a）浮动支座B侧向位移u的计算在要寻找的位移处，须在位移作用的方向上引入一个单位力“1”。（续）练习图18-4 在支座B上带有从属力矩变化的标准单位单元
如练习图18-1所示的框架承受分布载荷。对此，须通过做功原理以及由此得出的如下关系来确定变形：
其中，i为力“1”的位置；k为实际载荷的位置。
这里要特别注意的是，应采用合适的坐标系来进行计算。
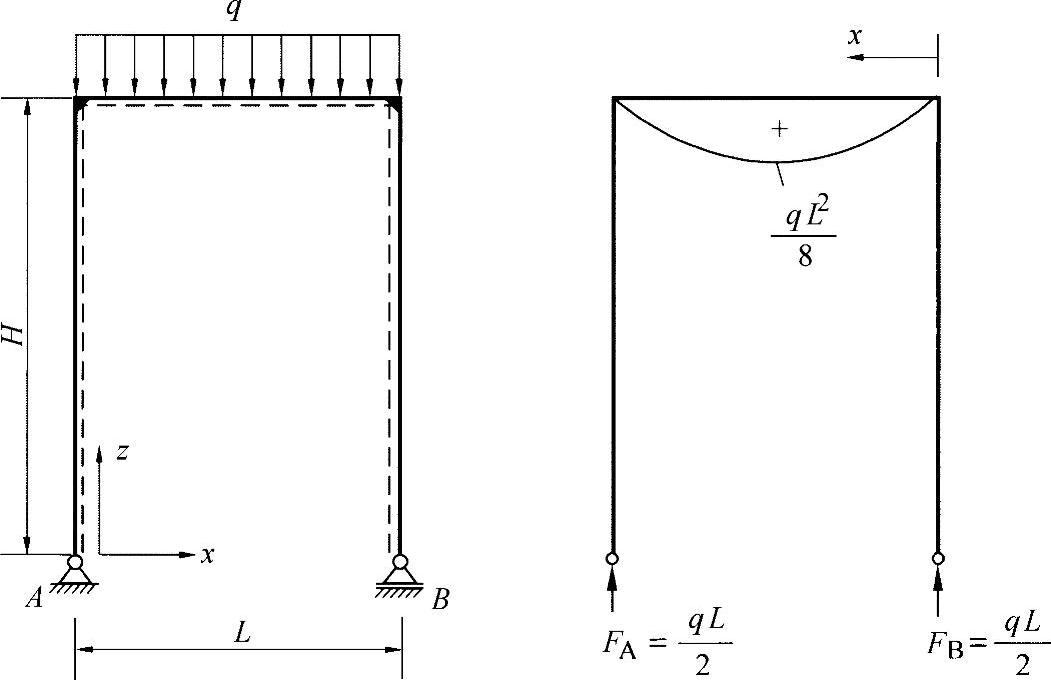
练习图18-1 框架与力矩面积
a）浮动支座B侧向位移u的计算
在要寻找的位移处，须在位移作用的方向上引入一个单位力“1”。练习图18-2中所示的弯曲力矩变化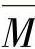
就是该单位力作用的结果，该力矩应分段并必须采用框架的实际弯曲力矩变化M进行叠加。
为了确定浮动支座的位移，可如下应用和评估做功原理：
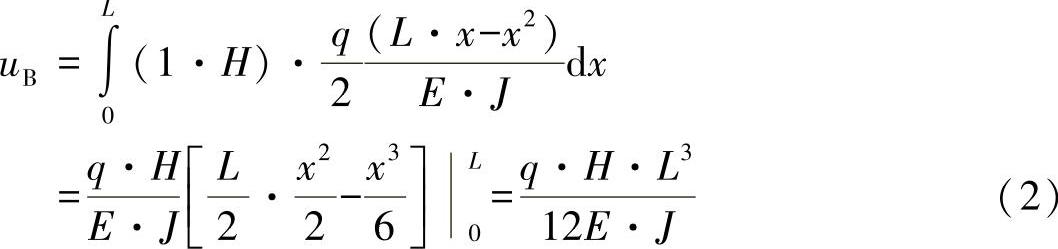
b）框架中心的挠曲wM的计算
如前面所示，此种载荷情形也可产生力矩变化，如练习图18-3所示。
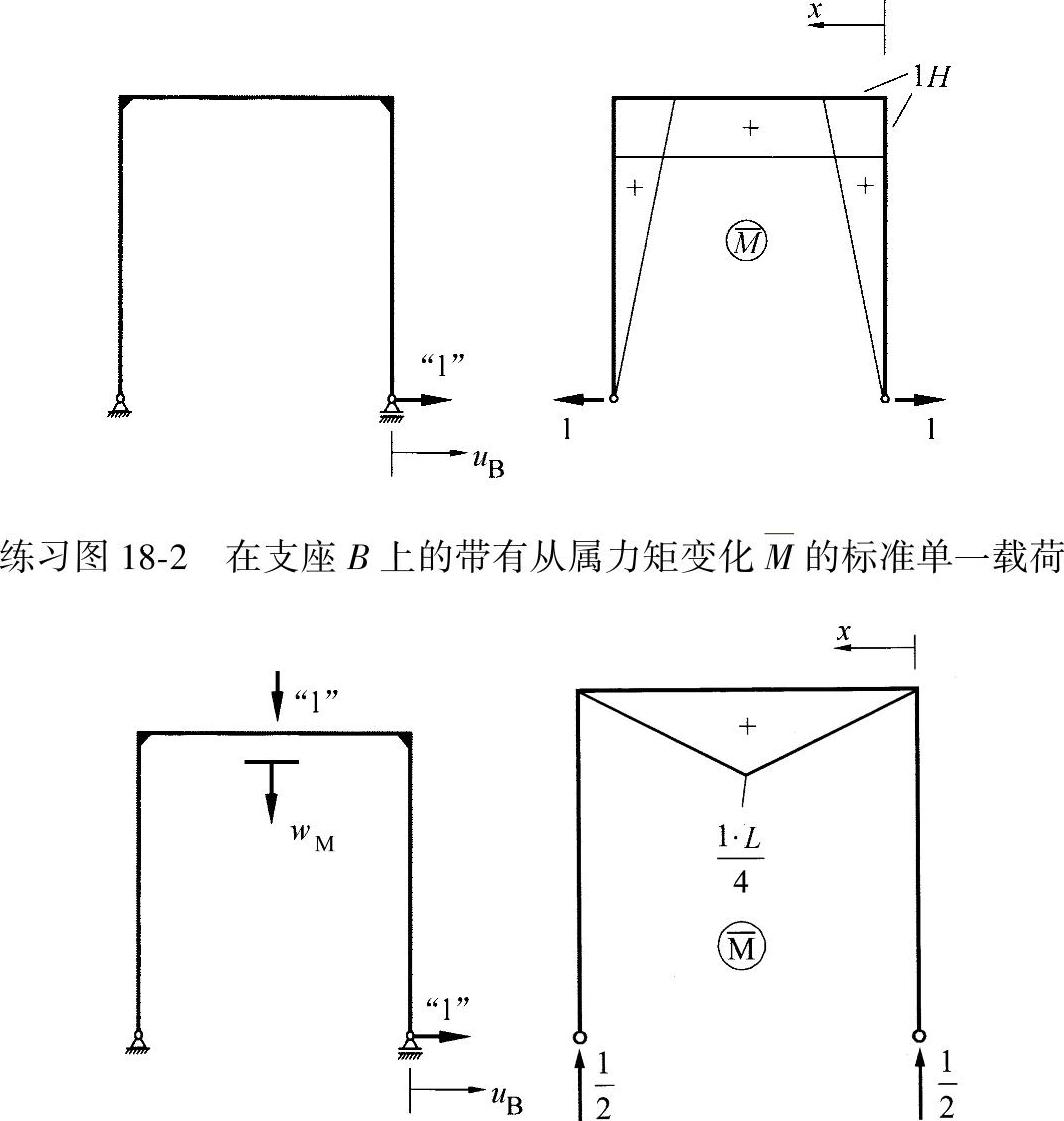
练习图18-3 在框架中心带有从属力矩变化M的标准单一载荷(www.xing528.com)
因此，可计算出挠曲为
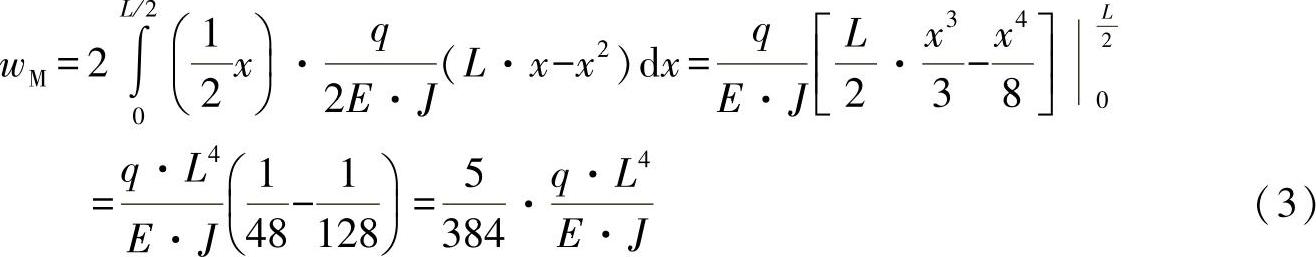
c）支座B处支架横截面倾斜ψ的计算
如练习图18-4所示，为求解这种载荷情形，须在框架的扭转方向上引入一个单位力矩，并考察力矩的变化。
因此，可以求出扭转为
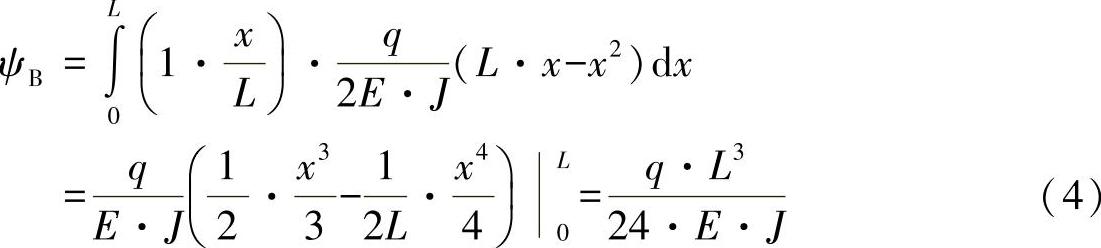
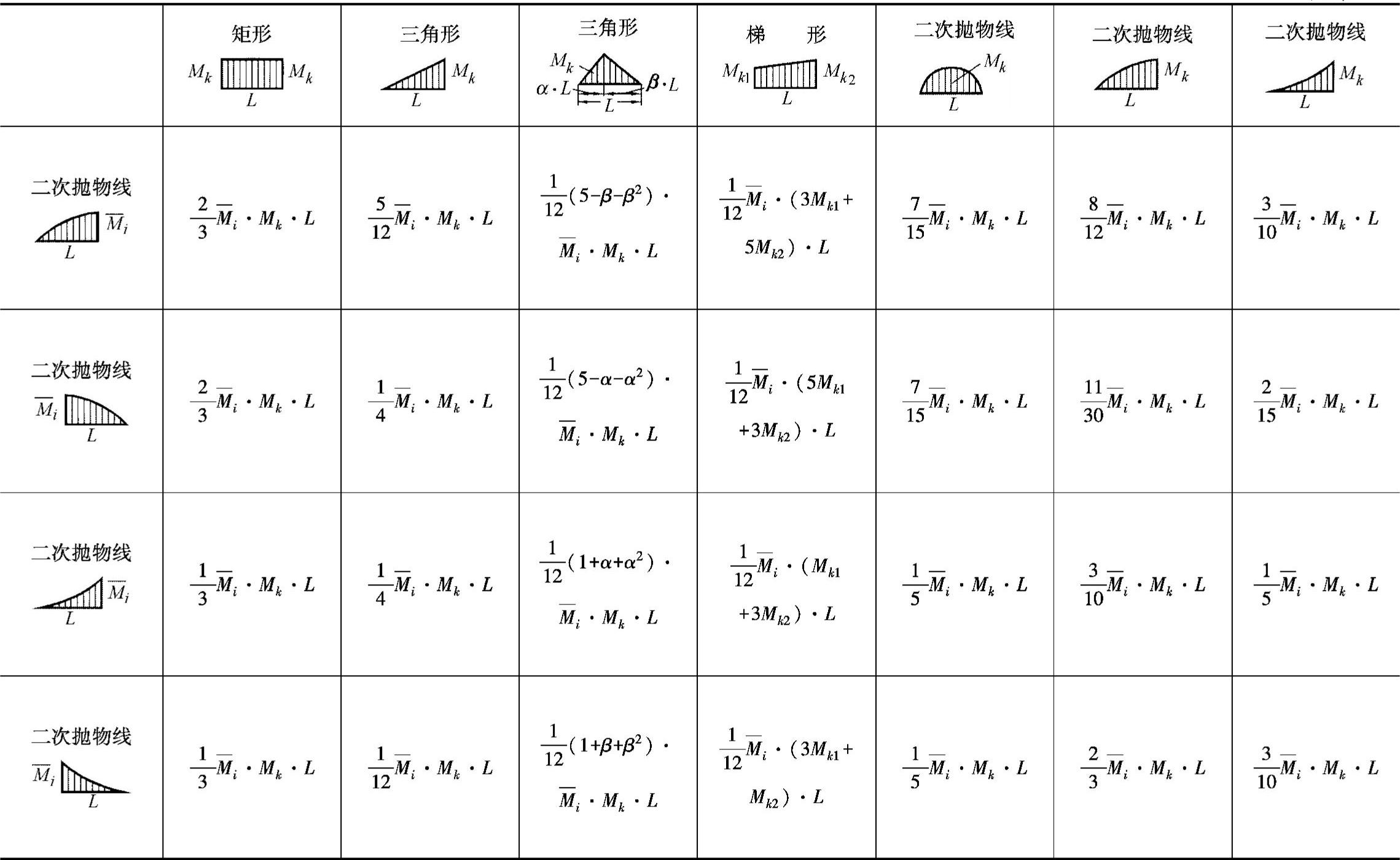
d）前面得到的单一结果也可以不通过积分的方法，而是借助下表求出。所有的变形值大小都可以通过相应的力矩面积的叠加而得出。
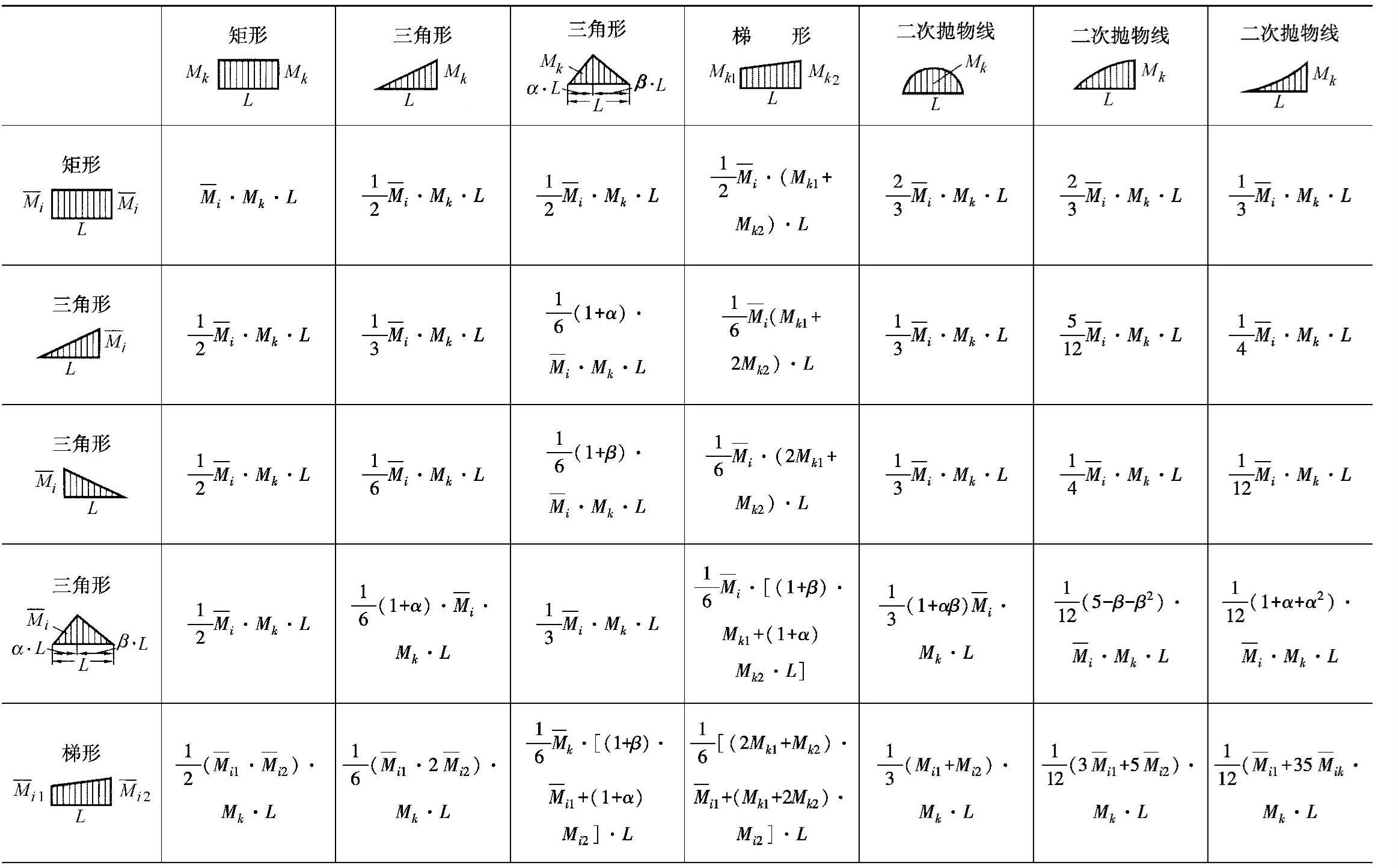
（续）
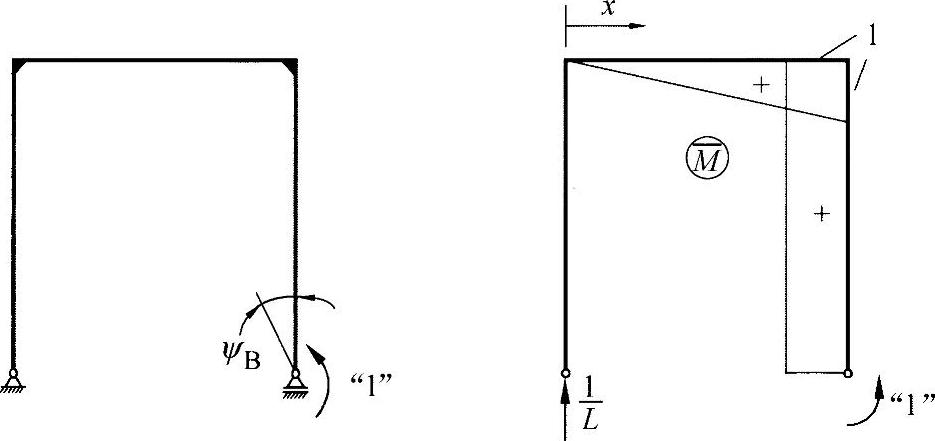
练习图18-4 在支座B上带有从属力矩变化的标准单位单元
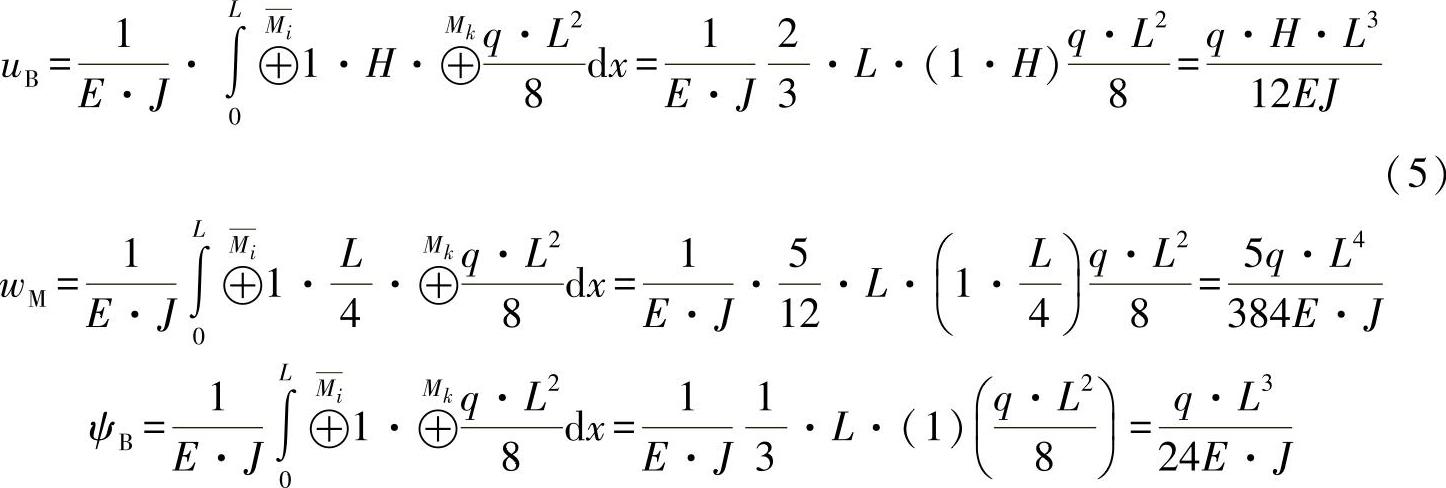
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
