【摘要】：对于练习图17-1中所示的悬臂梁，利用被动变形功求出弯曲线。对于弯曲情形，有如下关系：由此可以得出在位置处xi的挠曲wi。xi点是虚拟力“1”的作用点。Mb为真实作用载荷的弯曲力矩变化，Mb是由虚拟力“1”得出的弯曲力矩变化。w用0≤xi≤L作为变量值来描述弯曲线。真实弯曲力矩变化与真实曲率变化κ在力导入的a处产生了压弯，因此，须在两个区间内描述弯曲线，即wi与wi。
对于练习图17-1中所示的悬臂梁，利用被动变形功求出弯曲线。
悬臂梁在位置a处承受单一力F，力作用于型梁的剪切中心。
对于弯曲情形，有如下关系：
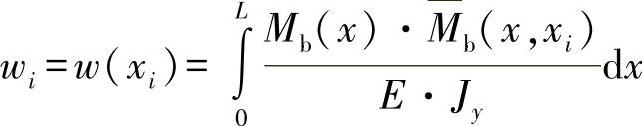
由此可以得出在位置处xi的挠曲wi。xi点是虚拟力“1”的作用点。Mb（x）为真实作用载荷的弯曲力矩变化，Mb（x，xi）是由虚拟力“1”得出的弯曲力矩变化。w（xi）用0≤xi≤L作为变量值来描述弯曲线。真实弯曲力矩变化与真实曲率变化κ在力导入的a处产生了压弯，因此，须在两个区间内描述弯曲线，即wi（0≤xi≤a）与wi（0≤xi≤L）。
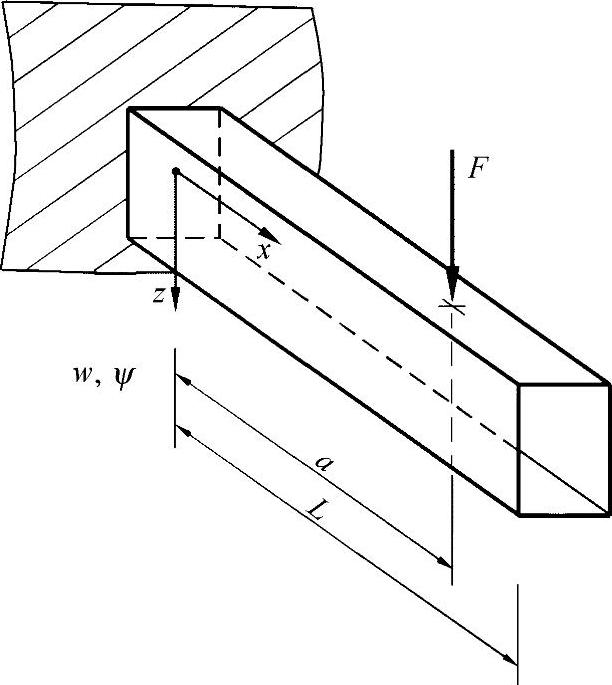
练习图17-1 承受单一力F的悬臂梁
如练习图17-2所示为在区间0≤戈，≤n的弯曲线
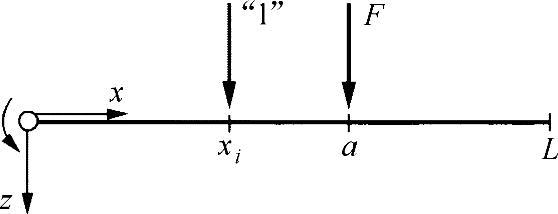
练习图17-2
弯曲力矩Mb（x）的变化为
0≤x<xi：Mb（x）=-F·（a-x）
xi≤x≤a：Mb（x）=-F·（a-x）
a<x≤L：Mb（x）=0
弯曲力矩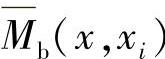
的变化为
如练习图17-3所示为在区间0≤xi≤L的弯曲线(www.xing528.com)
练习图17-3
弯曲力矩Mb（x）的变化为
0≤x<a：Mb（x）=-F·（a-x）
a≤x≤xi：Mb（x）=0
xi<x≤L：Mb（x）=0
弯曲力矩
的变化为
a<x≤L：Mb（x，xi）=0
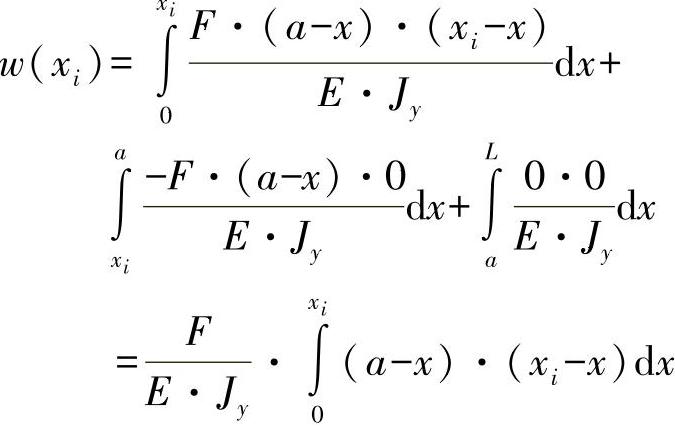
对0≤xi≤a，有
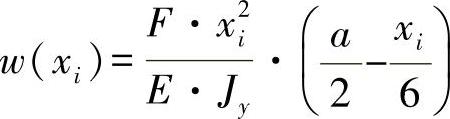
a<x≤L：Mb（x，xi）=0
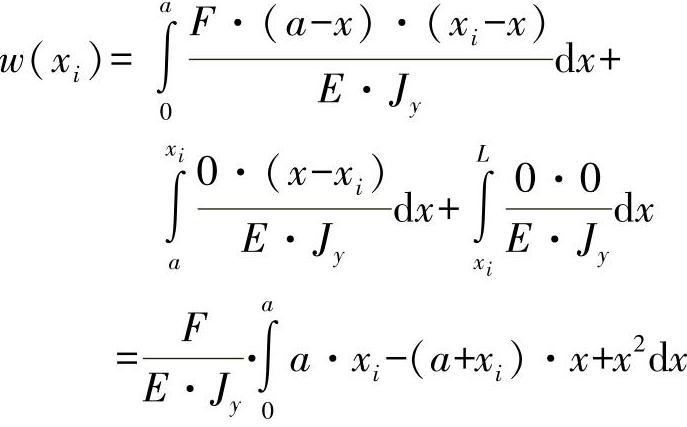
对a<xi≤L，有
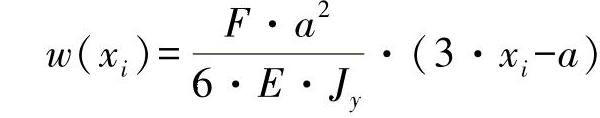
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
