【摘要】：针对变形功，本节将考察承受单一外力的封闭框架，如练习图16-1所示，以求出在水平桁梁段的中心面上的弯曲力矩。练习图16-1 承受压力的封闭框架在15.1节中阐明了，一个弹性体的变形功可广义表示为将此方程应用于本节所示的问题，则可以导出方程式：由于本节中所要讨论的框架为双对称性的框架，因此，只需考察四分之一的框架就可以了。为此，在要求解的力矩处将框架切开，并且将得到的内力作为外力引入计算中。
针对变形功，本节将考察承受单一外力的封闭框架，如练习图16-1所示，以求出在水平桁梁段的中心面上的弯曲力矩。
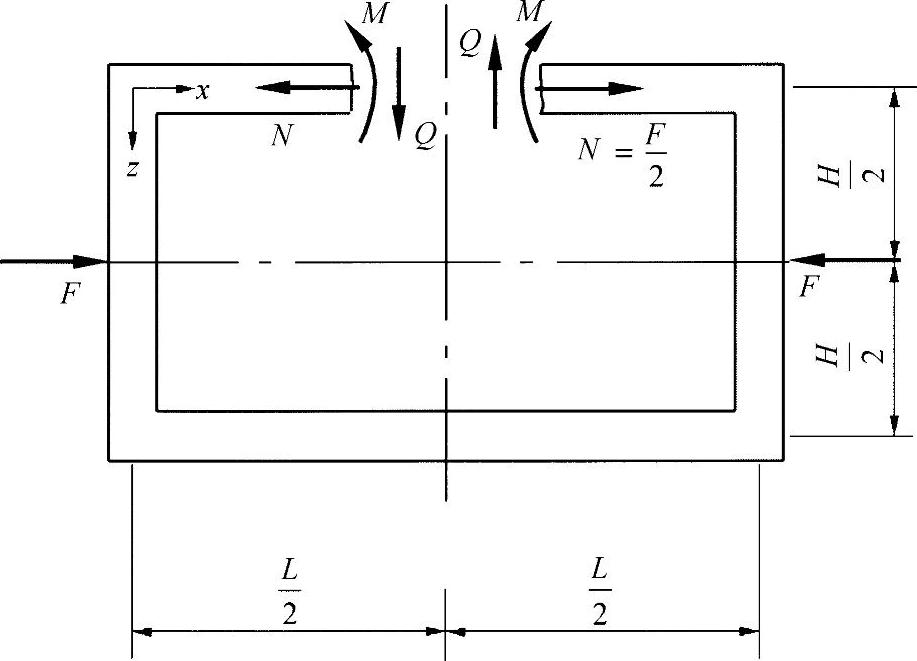
练习图16-1 承受压力的封闭框架
在15.1节中阐明了，一个弹性体的变形功可广义表示为
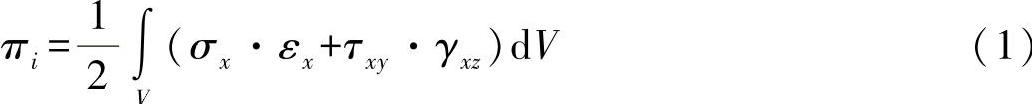
将此方程应用于本节所示的问题，则可以导出方程式：
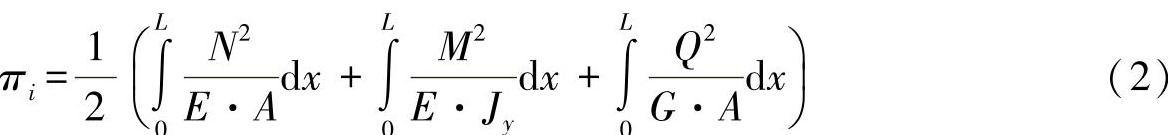
由于本节中所要讨论的框架为双对称性的框架，因此，只需考察四分之一的框架就可以了。
为此，在要求解的力矩处将框架切开，并且将得到的内力作为外力引入计算中。由于要处理的是围绕对称线的中心面，则可去掉反对称内力。在本例中，可求出剪力Q。借助平衡条件，即可以算出法向力。
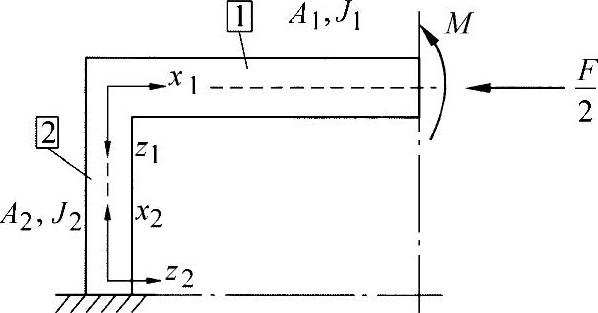
●切割桁梁的描述：
如练习图16-2所示，桁梁段上的内力为
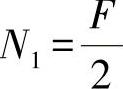
Q1=0
M1=M
N2=0
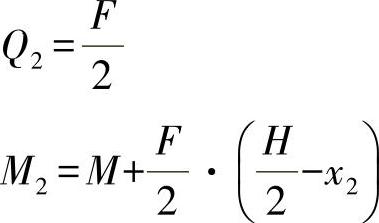
●桁梁段1在变形功上的分量：
(www.xing528.com)
练习图16-2 受力的桁梁段
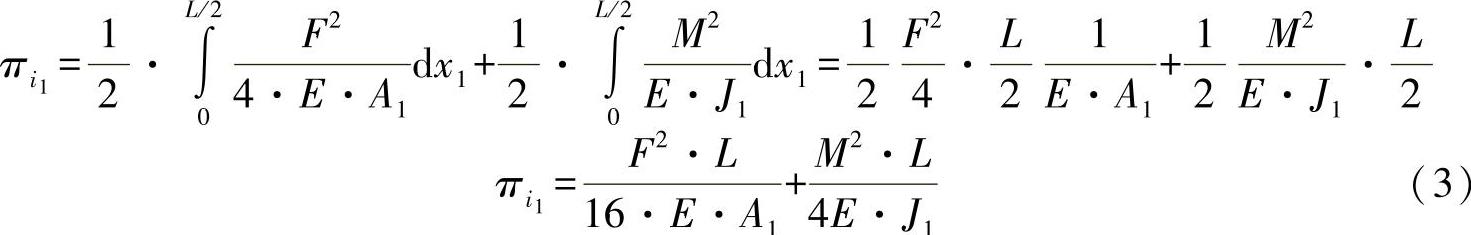
●桁梁段2在变形功上的分量：
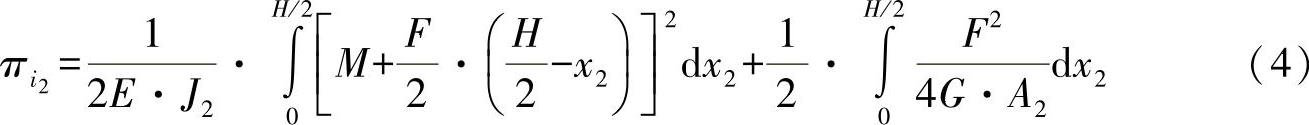
积分可有：
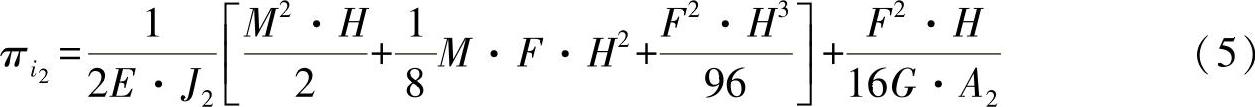
所计算的四分之一框架的变形功可归纳如下：
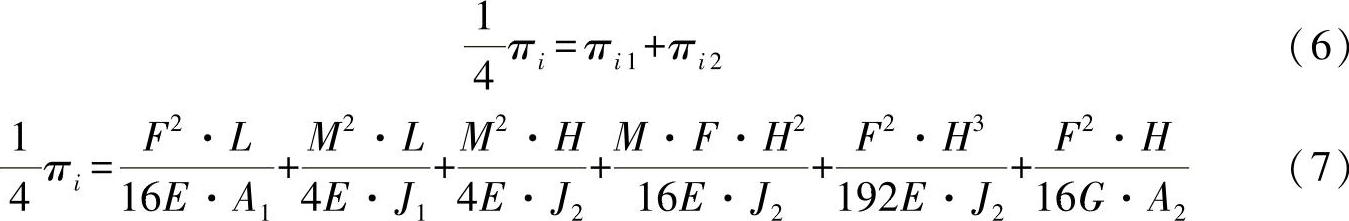
为了求解未知力矩，现在应用卡式最小功定理，该定理为
根据受力（一个力矩）的外功的部分求导，可以得出在力作用点上沿这个力（这个力矩）的方向上的位移（旋转）。
由于框架在固定截面位置上不允许裂开，所以，这里要求位移须等于零。
将这一定理用于方程式（7），则有：
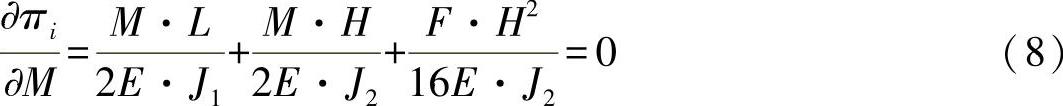
与
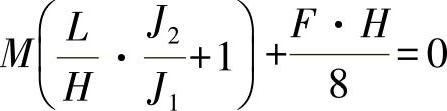
最后可得出力矩为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
