轻量化设计：翘曲阻力演练成果

如练习图13-1所示，当一个固定的型梁承受端面扭转力矩时，会在固定支座处产生翘曲阻力。这里要求出由纯扭转和翘曲力扭转产生的要传递的分量。

10.6节中已经证明了，在翘曲阻力作用下，外扭转力矩通过两个分量得以传递，对应于以下公式：

M_x=M_xt+M_xT （1）

或者微分方程：

E·C_W·ϕ‴-G·J_t·ϕ′=-M_x （2）

经过转换，可得出：

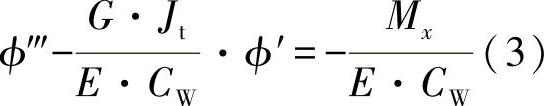
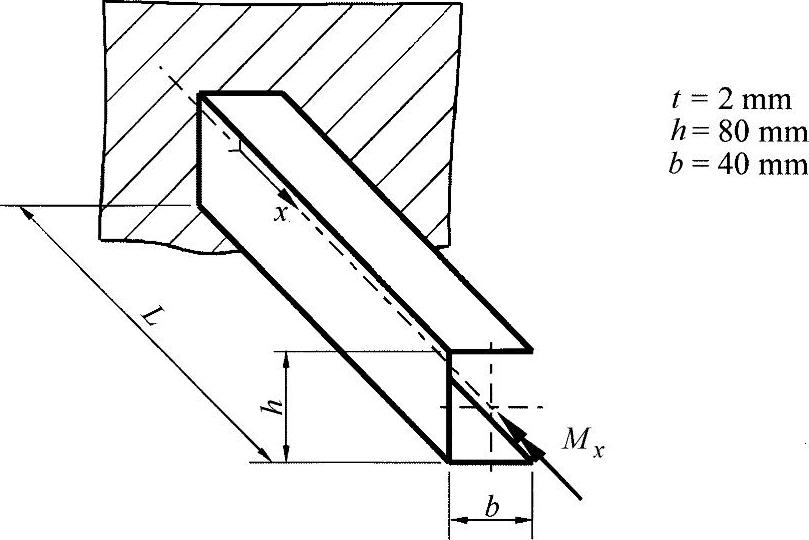
练习图13-1 承受翘曲阻力的扭转型梁

或者有标准形式：

ϕ‴-α²·ϕ′=-μ （4）

对于该不均匀微分方程，其均匀的和部分的解都是已知的，即：

ϕ_h=A+B·coshα·x+C·sinhα·x （5）

由边界条件可以得出：

1）x=0：ϕ（0）=A+B=0

2）

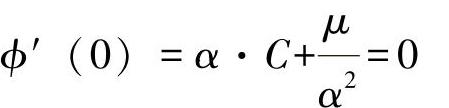
3）x=L：ϕ″（L）=α²·B·coshα·L+α²·C·sinhα·L=0

其中，

为常数，并得出：

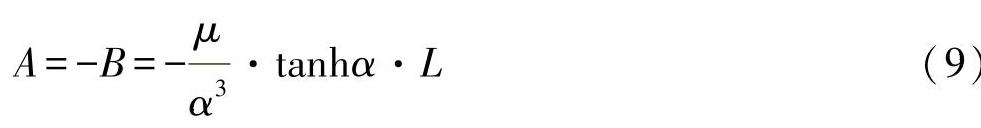
则微分方程（4）的解为

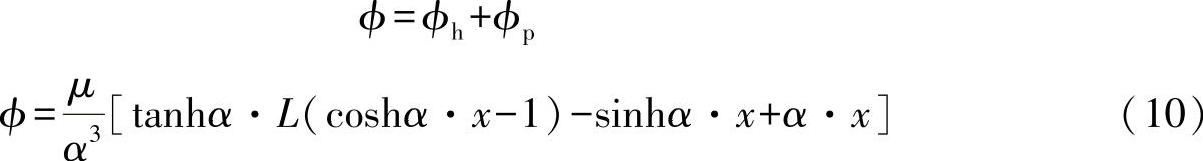
进一步对方程式（10）求导：

根据方程式（1），现在可以确定力矩分量，即有：

●圣维南扭转力矩分量：(https://www.xing528.com)

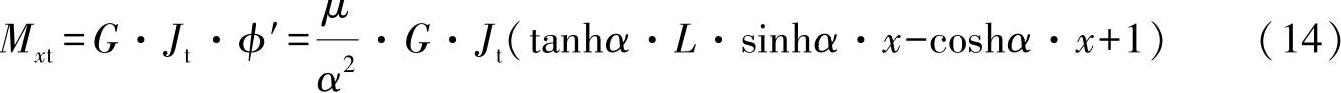
代入α²和μ，可以得出：

M_xt=M_x（tanhα·L·sinhα·x-coshα·x+1） （15）

●翘曲力扭转分量：

M_xT=-E·C_W·ϕ‴=-E·C_W·μ（tanhα·L·sinhα·x-coshα·x） （16）

代入_μ，可以得出：

M_xT=-M_x（tanhα·L·sinhα·x-coshα·x） （17）

为了能够讨论翘曲阻碍的影响，必须进一步求出：

其中，

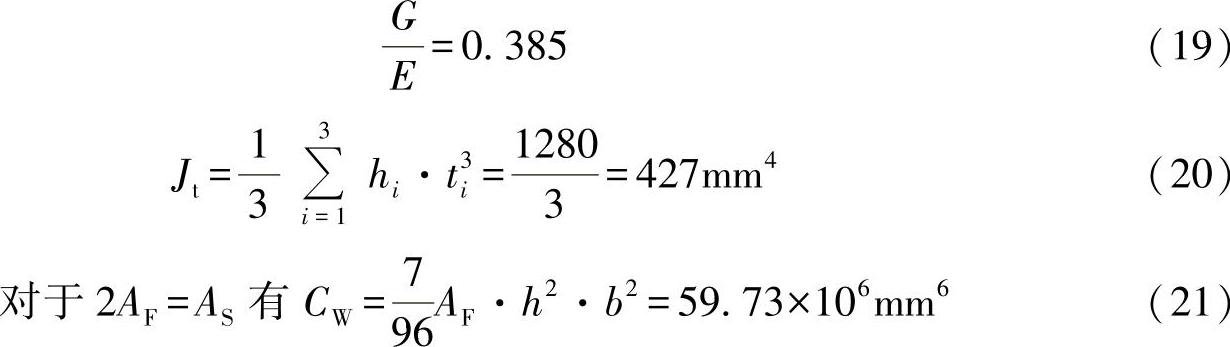
代入方程式（18），则有：

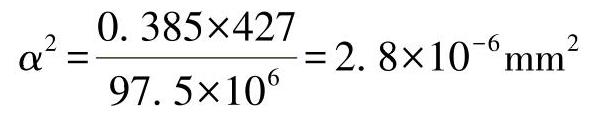
与

α=1.6×10^-3mm^-1（22）

经过以上推理，现在可以对方程式（15）和（17）进行评估了。不过，如果将带有ξ=x/L的纵向坐标加以标准化，会更好一些。为此，可将上述方程表示为

M_xt=M_x（1-η） （23）

其中，η=coshα_i·ξ-tanhα_i·sinhα_i·ξ；α_i=1.6×10^-3·L_i。

M_xT=M_x·η （24）

更重要的是比例关系：

在标准长度上对_η的评估结果见练习图13-2。

练习图13-2 沿杆轴向上的力矩变化

可得出结论，在较短的长度上，翘曲的影响是主要的。

对于所有的杆来说，翘曲力矩主要出现在固定位置处，而在力作用位置处起主要作用的则是圣维南扭转。