【摘要】:下面两图所示为两个薄壁的、承受纯扭转载荷的管,第一个是开口的、沿轴向切开的型材;第二个是闭口的型材。练习图9-1 开口薄壁管练习图9-2 闭口薄壁管如练习图9-3所示,首先考察在扭转应力载荷Mx作用下的一个细长矩形横截面。按照方程式和式,切应力的比例为在闭口型材中的最大切应力明显小于在开口型材中的最大切应力。所以,在可能的情况下,应优先采用闭口型材,而不是开口型材的设计。
下面两图所示为两个薄壁的、承受纯扭转载荷的管,第一个是开口的、沿轴向切开的型材(练习图9-1);第二个是闭口的型材(练习图9-2)。这里对管的承载能力和变形能力进行比较。管的固定方式须确保自由翘曲。

练习图9-1 开口薄壁管

练习图9-2 闭口薄壁管
如练习图9-3所示,首先考察在扭转应力载荷Mx作用下的一个细长矩形横截面。
按方程式(10.3)(对于扭转)有:

在方程式(10.10)中,当t<<b,则矩形扭转惯性矩为

由此,可以得出扭转为

当t<<b时,扭转阻力矩Wt为

这里,切应力τ0可以直接求出:

练习图9-3 细长矩形截面
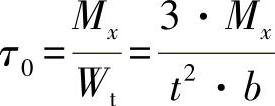
根据方程式(2)进行类推,则轴向开口管横截面的扭转惯性矩为

据此,可以求出扭转为(https://www.xing528.com)

以及切应力:

按照方程式(10.15),可计算出薄壁闭口管的扭转惯性矩为

扭转则为


练习图9-4 在开口截面与闭口截面下扭转的比例
对于闭口管,按照10.2节,其初始假设可为薄壁,并且切应力在壁厚上是均匀分布的,则有:

比较开口型材与闭口型材:
扭转比例为

由于rm>>t,开口型材的扭转比闭口型材大很多,练习图9-4所示为扭转的比例。
按照方程式(7)和式(10),切应力的比例为
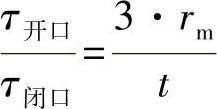
在闭口型材中的最大切应力明显小于在开口型材中的最大切应力。
基于扭转、变形和应力的比较,证明了闭口型材具有更好的性能。所以,在可能的情况下,应优先采用闭口型材,而不是开口型材的设计。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




