【摘要】:练习图7-1所示为一个底盘设计结构的悬臂梁,由于内部需要铺设液压导管,设计为开口型梁。当时,可得出静态矩:另外,还需求解基于y轴的面积惯性矩,对此有:现在,可以按照方程式确定剪切中心坐标ySM:b)请计算由在剪切中心SM处作用的剪力FZ引起的剪切力流与法向力流!
练习图7-1所示为一个底盘设计结构的悬臂梁,由于内部需要铺设液压导管,设计为开口型梁(练习图7-2)。
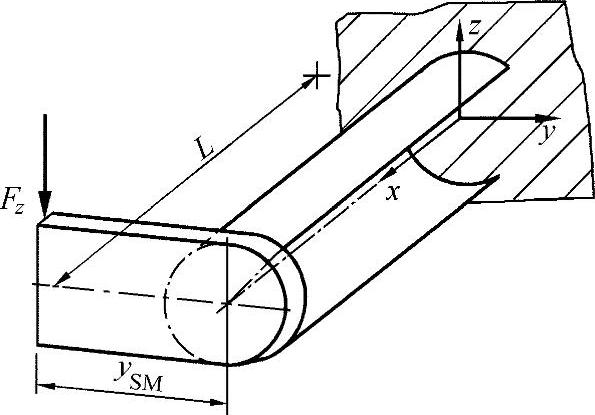
练习图7-1 底盘设计结构中的悬臂梁
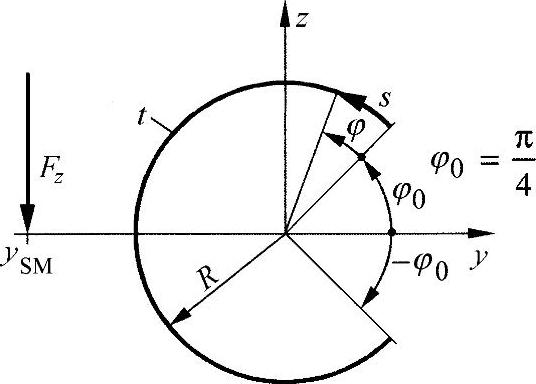
练习图7-2 部分圆型材
a)图中所示的剪切力FZ必须用哪个杠杆ySM作用在部分圆形型材上,从而不会产生扭转载荷?
对于剪切中心SM,通过a展开形成的积分为
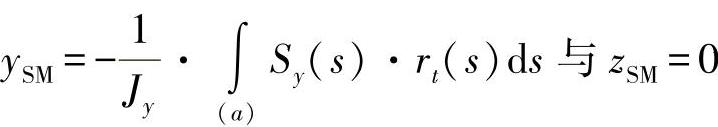
rT(s)是切线的距离(最小距离),从起点(坐标原点)出发通过型材中心线上的点s。在圆上,rt(s)=R。这里,用圆弧角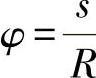 代替圆弧坐标s。通过s=φ·R与ds=R·dφ进行替代,可以得出:
代替圆弧坐标s。通过s=φ·R与ds=R·dφ进行替代,可以得出:
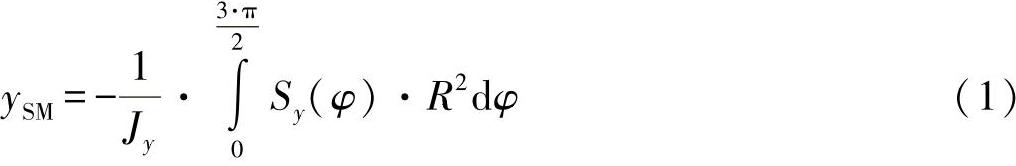
直至圆弧坐标s形成的不完整静态力矩为
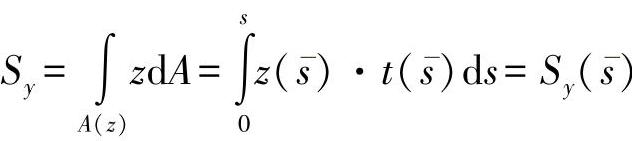
这里,也采用s=φ·R与ds=R·dφ替代圆弧坐标s,即:
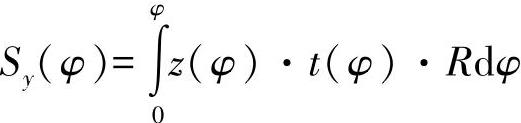
对于坐标z与角φ的相关性,按照练习图7-2有:
z(φ)=R·sin(φ+φ0)=R·(sinφ·cosφ0+cosφ·sinφ0)沿圆弧长度s与角φ上的型材厚度t为常数。当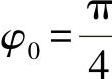 时,可得出静态矩:
时,可得出静态矩:
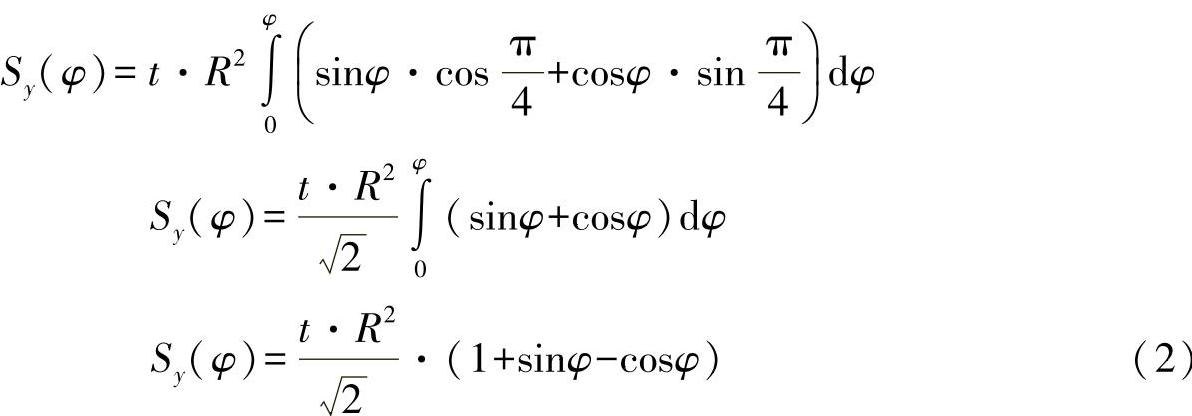
另外,还需求解基于y轴的面积惯性矩,对此有:
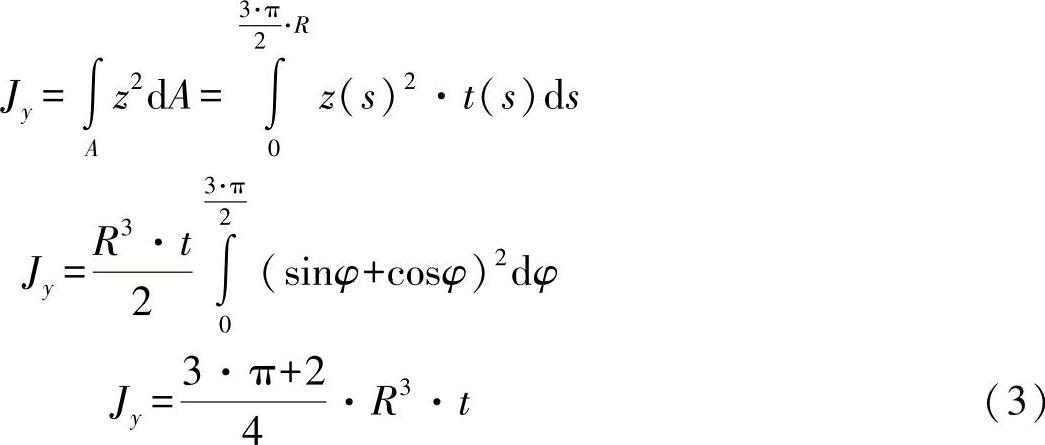 (https://www.xing528.com)
(https://www.xing528.com)
现在,可以按照方程式(1)确定剪切中心坐标ySM:
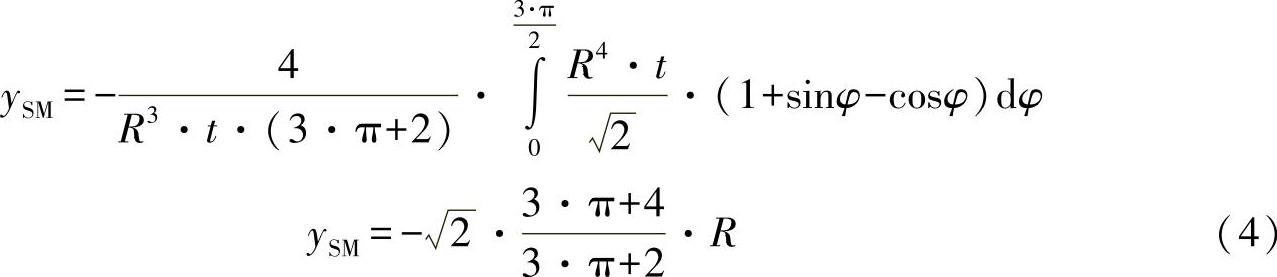
b)请计算由在剪切中心SM处作用的剪力FZ引起的剪切力流与法向力流!在图中所示的坐标系中,剪切力流为
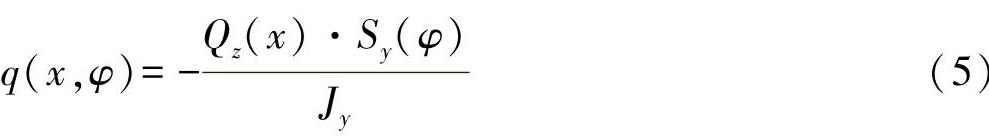
在悬臂梁上的内力变量为
QZ(x)=-Fz与Mby(x)=Fz·(L-x)
将方程式(2)与式(3)代入方程式(5)可得出:
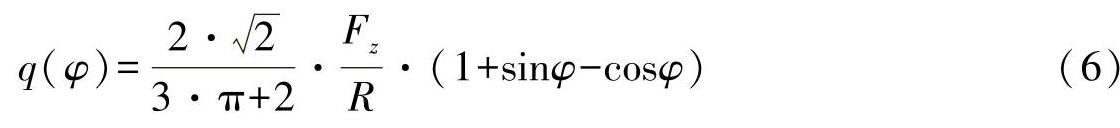
法向力流可由下式确定(举例):
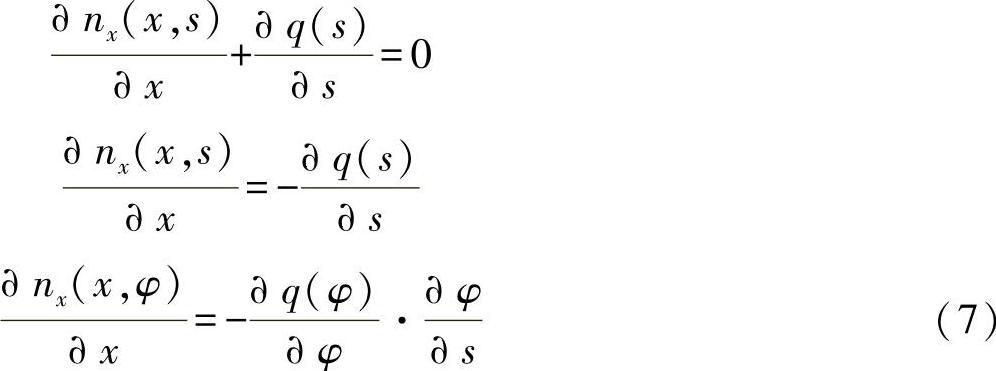
其中,
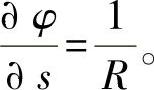
由方程式(6)得出:
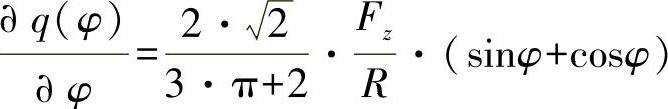
由此,对方程式(7)可有:
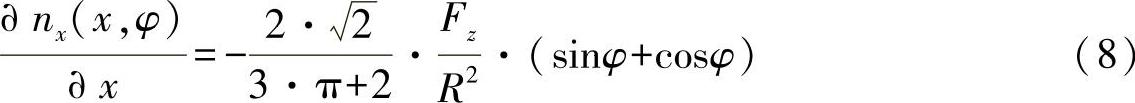
经过一次积分,并且考虑到在自由桁梁终端的边界条件nx(x=L,φ)=0,最后可以求得法向力流为
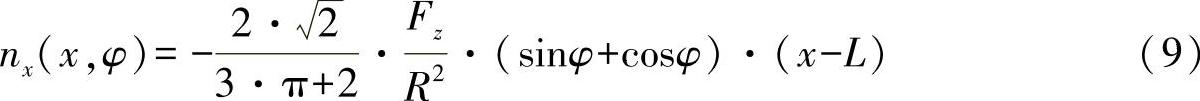
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




