轻量化设计：计算基础与构件结构-盘单元练习

对于盘，在方程式（8.57）中已经推导出微分方程为

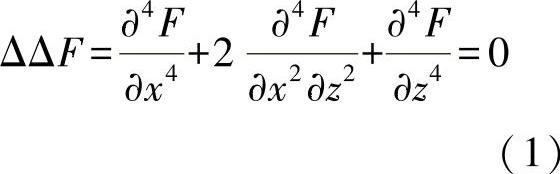
下面将以一个悬臂盘为例，来说明如何应用应力函数。对于练习图6-1中所示的例子，须确定内力变量。

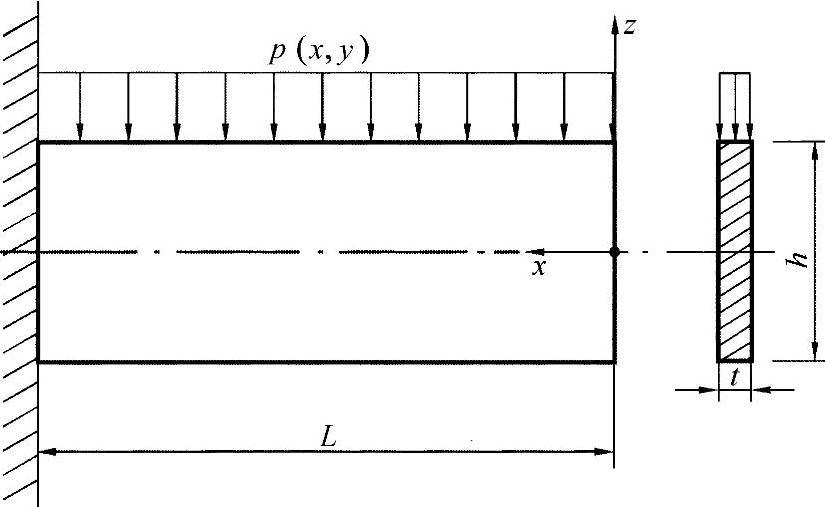
练习图6-1 在面积载荷下固定的盘

该示例中的边界条件（注意坐标系）为

对于x=0： n_x=0， q_xz=0 （2a）

对于x=L： u（L）=0， w（L）=0 （2b）

对于z=+（h/2）： n_z=-p·t， q_xz=0 （3a）

对于z=-（h/2）： n_z=0， q_xz=0 （3b）

选择应力函数系数时，应当尽可能准确地满足方程式（1）及边界条件。这里还假设，不考虑边界条件式（2b）。

对于爱黎应力函数，可生成一个双位公式，即有：

F=a₂₀·x²+a₂₁·x²·z+a₂₃·x²·z³+a₀₃·z³+a₀₅·z⁵ （4）

在系数a_ik处的第一个下角i表示x的指数；第二个下角k表示z的指数。

根据定义，利用所选择的方程，可求出内力变量为

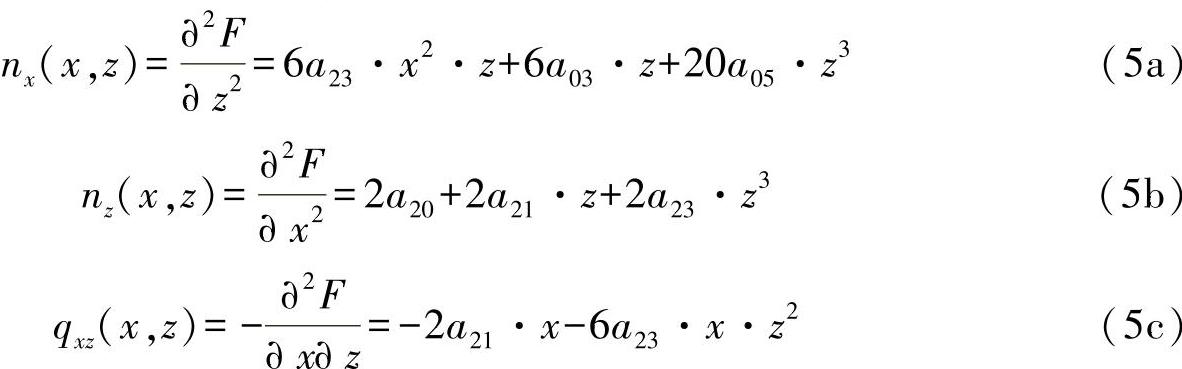
方程中出现的自由系数a_ik须如下确定，以满足盘的双位方程（1）和边界条件式（2）和式（3），即：

●由微分方程式（1）可得出：

a₂₃+5·a₀₅=0 （6a）

●由边界条件式（3a）和方程式（5b）可得出：

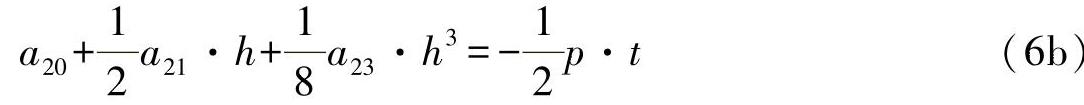(www.xing528.com)

●由边界条件式（3a）和方程式（5c）可得出：

●由边界条件式（3b）和方程式（5b）可得出：

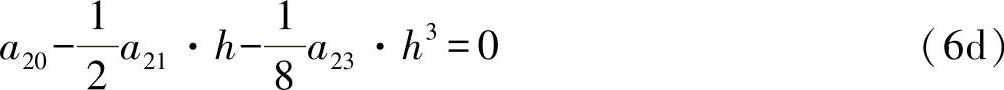
方程组（6）已经提供了系数的解：

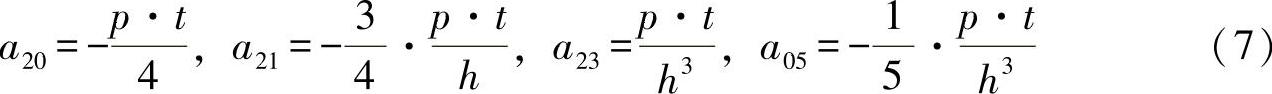
在方程式（3b）中，无法由第二个边界条件得出更多的信息。但是，还需要确定未知系数a₀₃。由边界条件（2a）可进行失效判断：

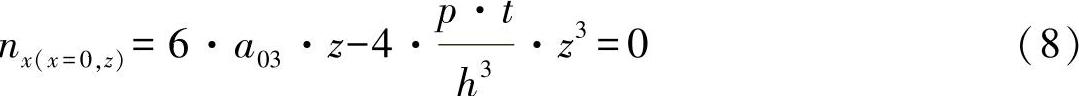
对于常数a₀₃，这一判断无法得到满足，因此，对于边界条件式（2a）需要有一个替代边界条件，以消除方程式（8）的要求。这样一个替代边界条件为

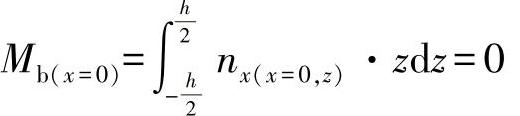
由方程求得的内力变量变化过程n_x（x=0，z）中的弯曲力矩M_b（x=0）应当消失在端面处（x=0）。由此，得出系数a₀₃为

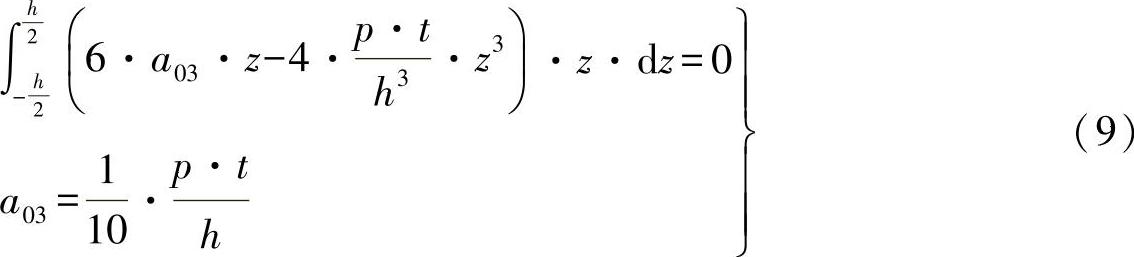
欲求解的内力变量为

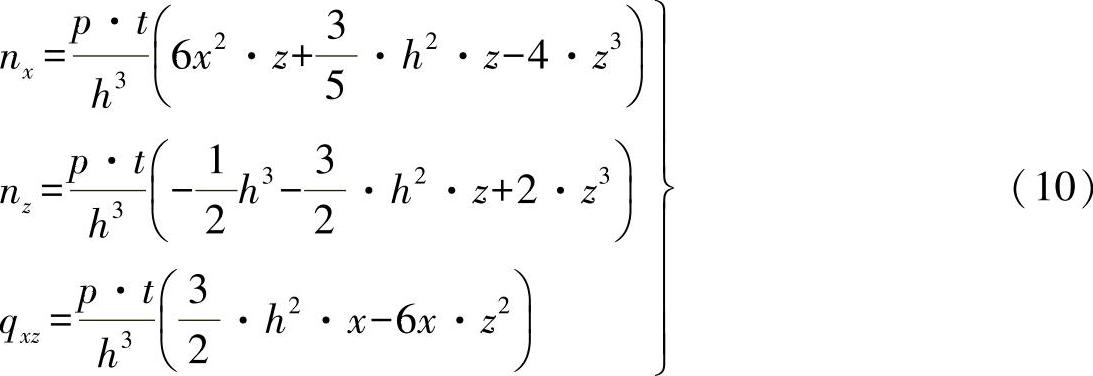
如果按照传统的梁弯曲技术理论，则只能得出法向力流：

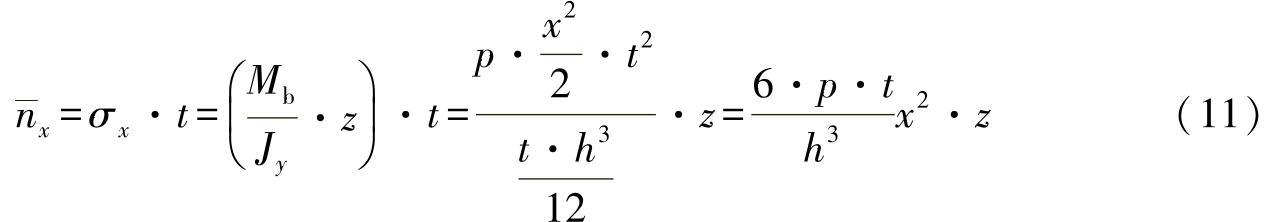
由此可以看出该方法与经典弯曲理论的区别。在练习图6-2中，表示出了发生的应力变化过程。从图中可以看到，在位置x=0处，边界条件n_x=0没有得到满足。

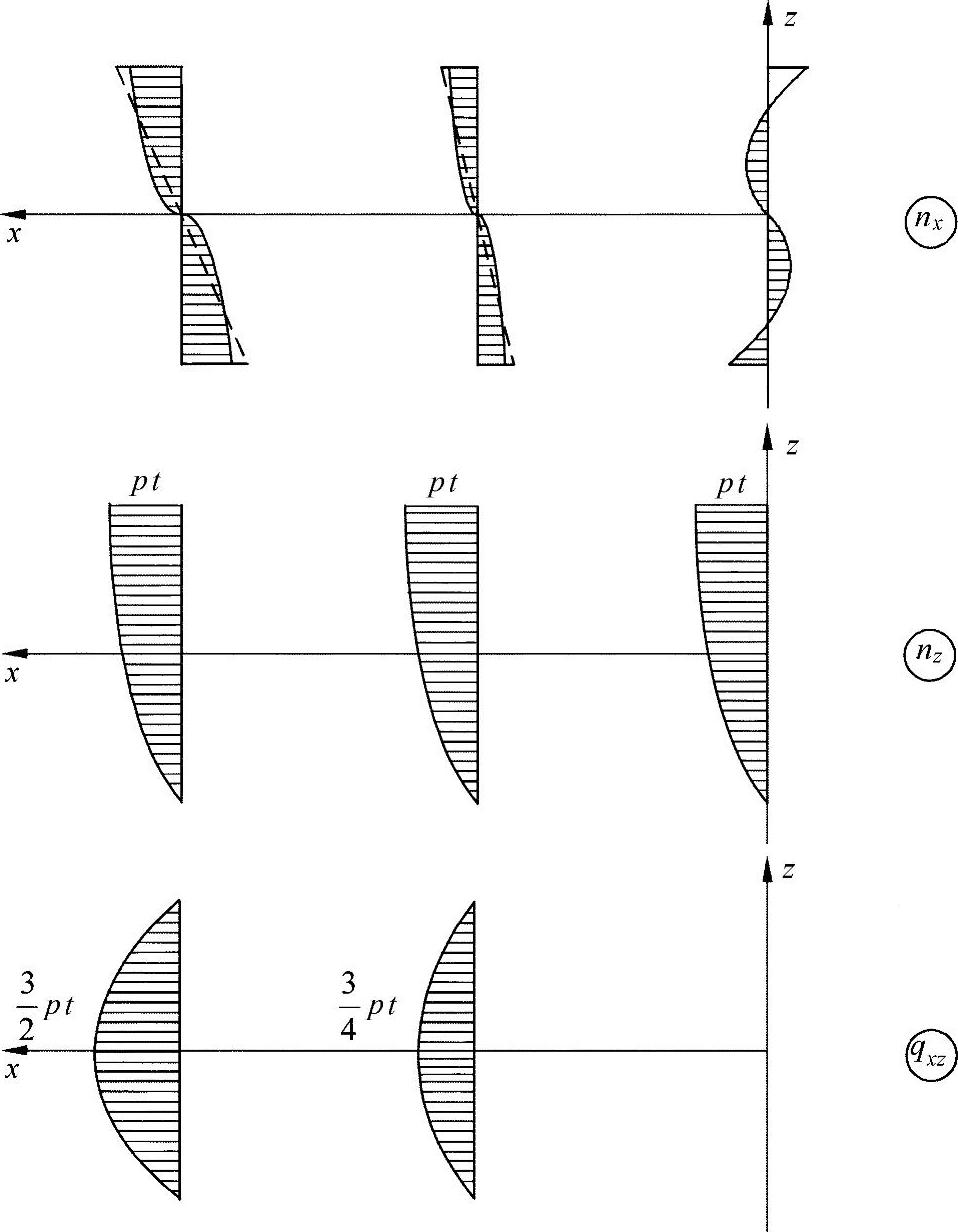
练习图6-2 在盘（——）与梁（----）上应力变化过程的对比