轻量化材料练习：计算基础与构件结构

在承载的板材设计结构中，越来越多地采用钢多层板材或者铝多层板材。板材的组合原则在于在使用性相同的情况下，具有明显的重量优势（减重约10%）。下面的例子用来阐述多层承载桁梁基础知识。

如练习图3-1所示，众所周知，在弯曲下的纤维的变形，可以用曲率半径（ρ）得出：

ds′=（ρ+z-z_o）·dϕ （1）

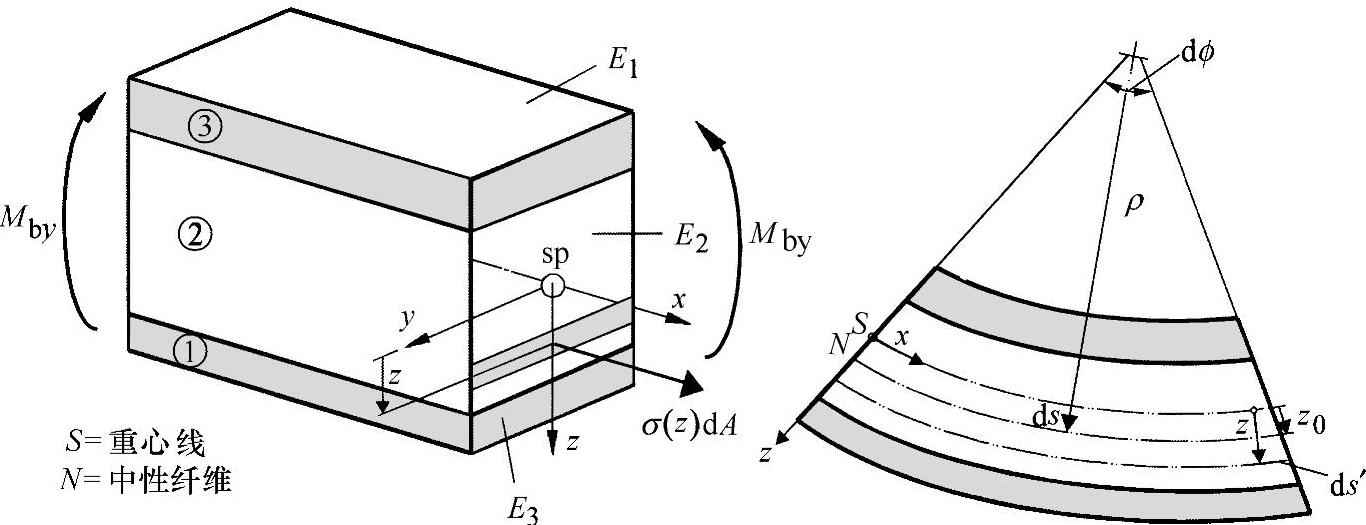
练习图3-1 具有冶金的、粘接或者辊轧层的复合桁梁的载荷

对于应变有：

对于应力有：

同样的，作为平衡条件可以列出如下方程：

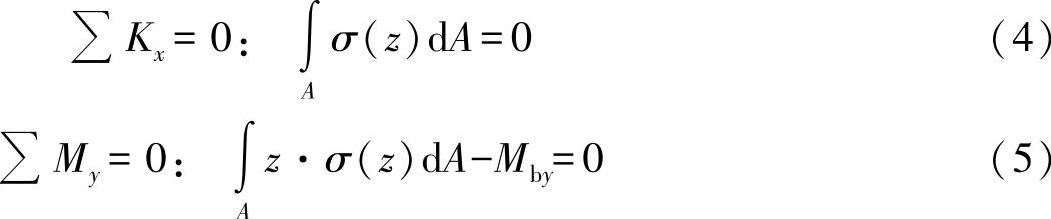
如果在这里代入方程式（3），对于方程式（4），则可进一步得出：

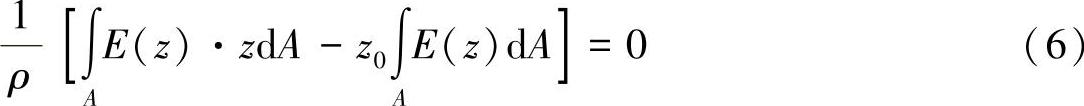
以及对于方程式（5）：

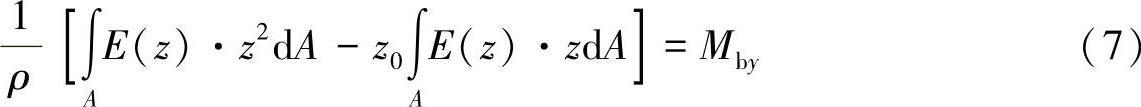
由于弹性模量在区域内是常数，积分也可以写成：

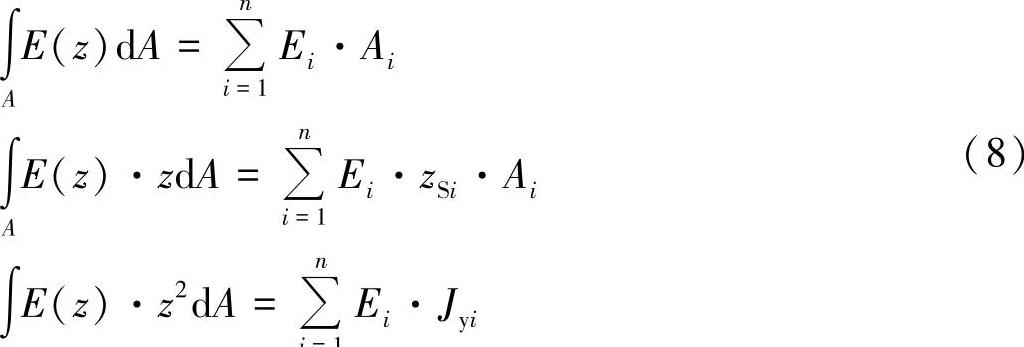
这里，可以用循环变量i求得每个子面积。因此，前面的方程式（6）、式(www.xing528.com)

（7）可以写成：

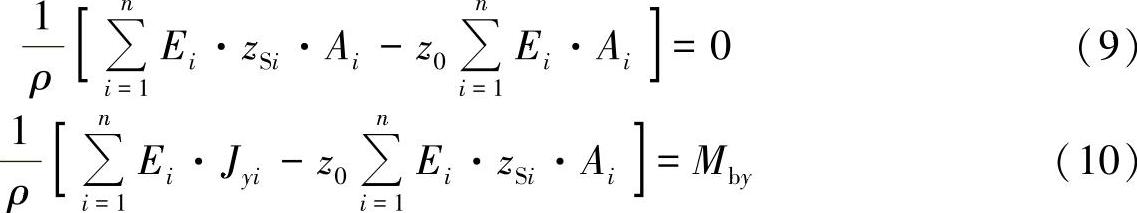
如练习图3-2所示，由方程式（9）可以得出重心的位置：

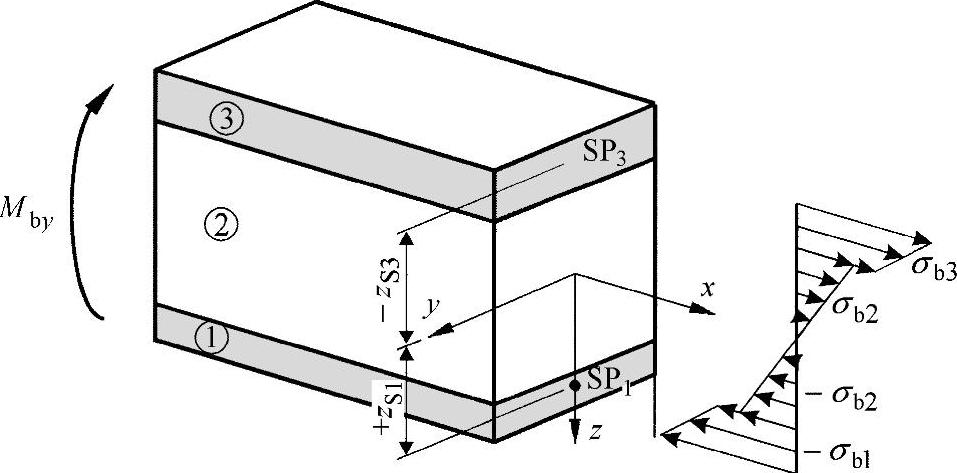
练习图3-2 重心的位置

并且，由方程式（10）得出桁梁的曲率：

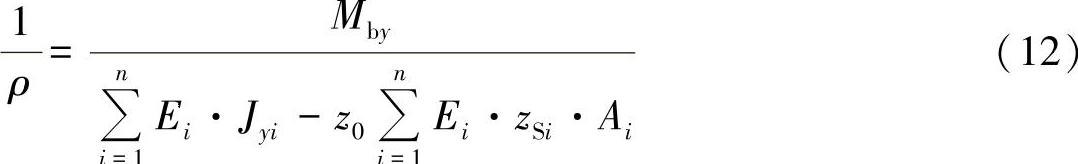
通过以上研究，可求得应力的分布为

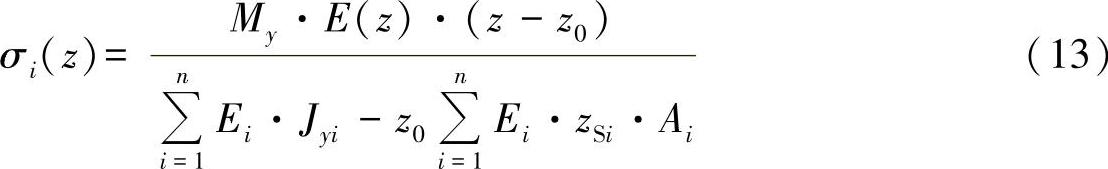
在中性的纤维中，该应力函数在z=z_O处的值为零。除此之外，在每个E_i=常数的材料领域中，函数与z一起产生线性变化。

通过曲率半径，可进一步得出挠曲的内在关系为

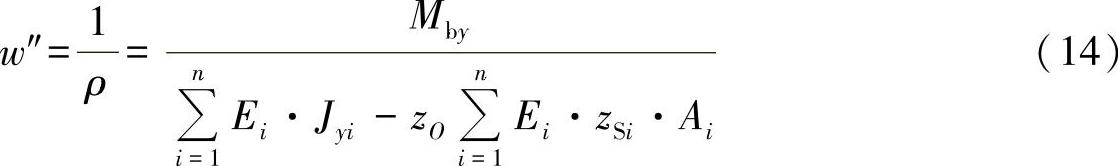
也就是说，由其二次积分可以确定该示例中的弯曲。

如今，在高级乘用车中，很多板材构件（发动机罩盖、盖、门板）都用到了铝多层板（例如Novelis公司的Fusion技术）。这些构件中大多数采用了两层或者三层的复合构造，以达到更好的强度、刚度和表面性能。练习图3-3中显示了Fusion技术的生产过程。

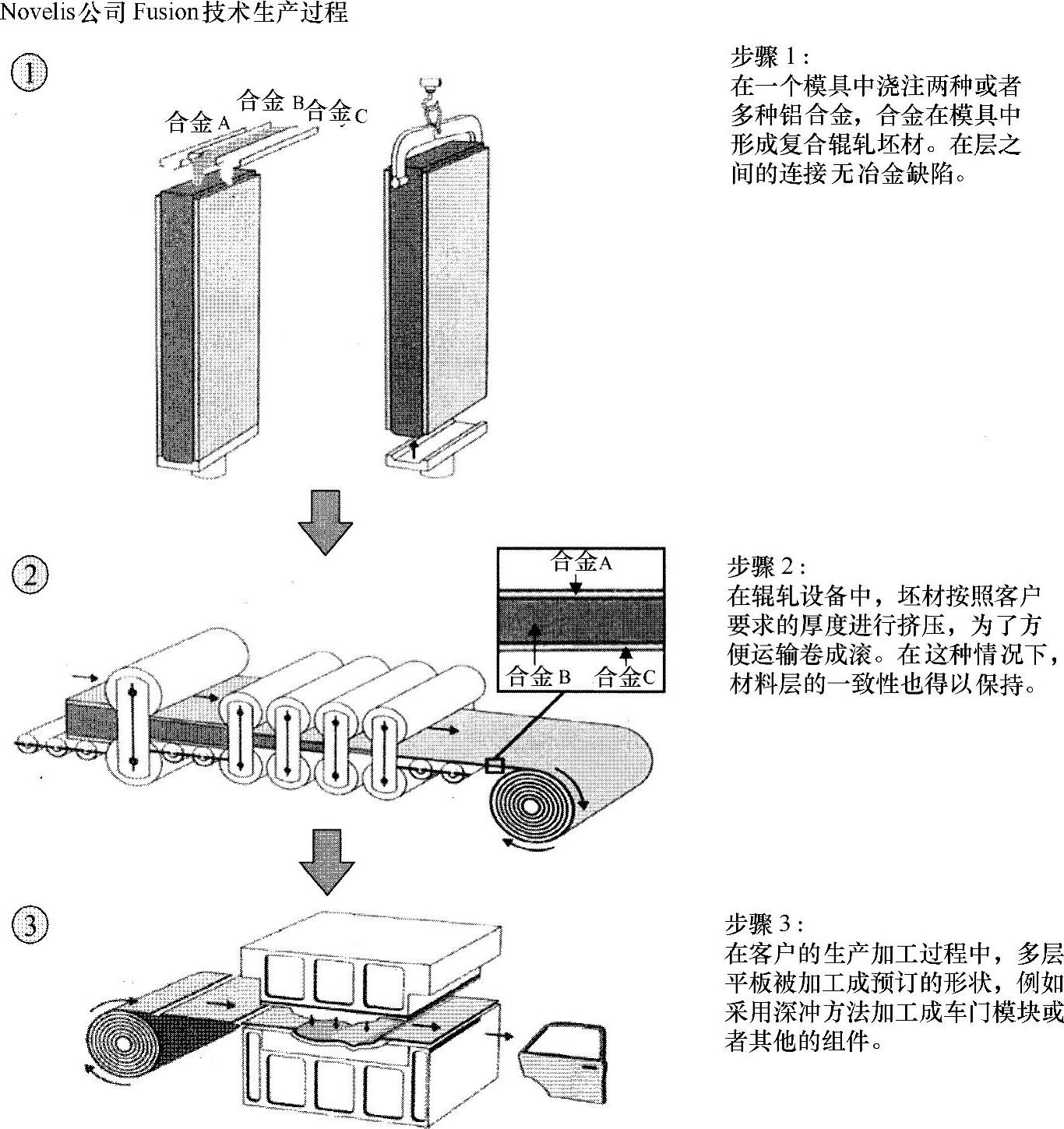
练习图3-3 铝多层板的制造与轧制成型（源：ATZ2/2007）