轻量化设计：材料选择准则与轻量材料练习

从轻量化的角度选择设计材料时，其基本的要求为

●保证功能（变形条件）；

●保证安全（持久性能）；

●满足重量要求（有效载荷/结构重量比例关系）；

●可加工性（可成型性/适于焊接）；

●生产成本（材料成本，加工成本）；

●维护成本（腐蚀保护，修理）；

●经受考验（采用新材料的风险）。

由于目标要求常常相互冲突，选择合适的材料比较困难，绝大多数情况下，必须做出妥协，以选择一个折中的方案。

为了能够采用量化的方法选择材料，可以研究对于钢或铝替代的使用限制条件。

2.1 低质量的优点

低质量的优点在承载的动态过程中体现得特别明显，可以用以下的例子加以证明。

2.1.1 回转件

回转部件产生的离心力：

F_z=m·r·ω² （1）

该离心力在部件的内部产生应力，其大小为

式中c——系统常数，

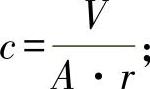
v——切线速度；

ρ——密度。

按照速度进行简化有：

其中c₁为一个新的常数。

结果表明，最大可达到的边界速度直接取决于材料的断裂系数。现在，可以将这一知识用在一个小的应用案例上。

示例：回转机械手

如练习图2-1所示，按照方程式（3），可以得出切线速度为

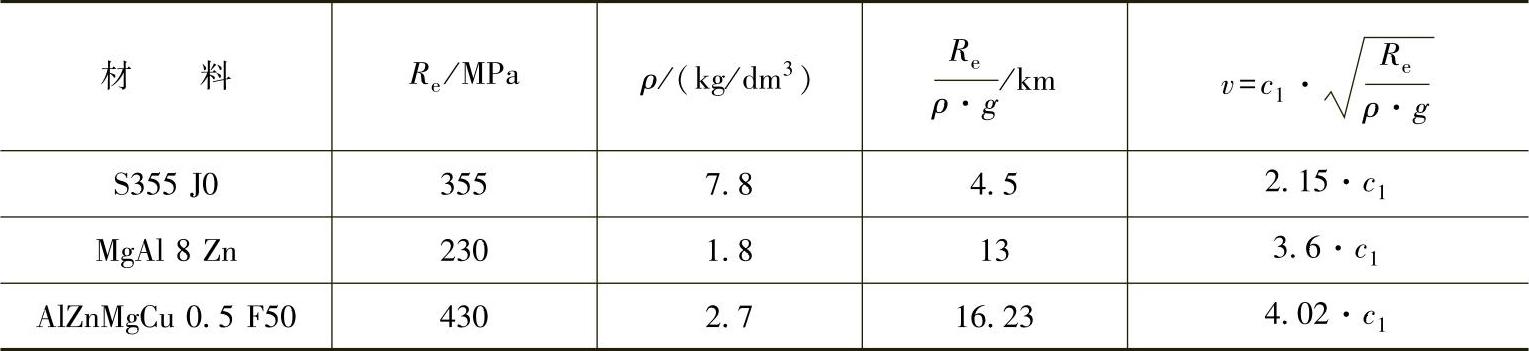
如果将材料的屈服强度R_e作为允许应力，从下表中可以看出，如采用铝替代钢，在相同的结构尺寸下，机械手的转速几乎增加了一倍。

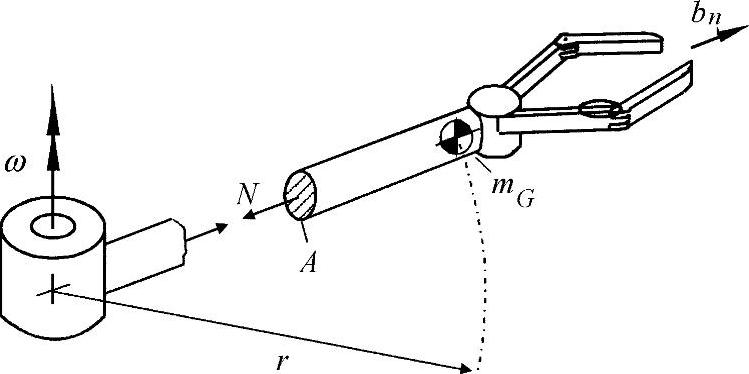
练习图2-1 机器人的机械手

2.1.2 振动件

在振动件中产生的力与材料的密度和加速度线性相关：

N=m_G·b=ρ·V·b=ρ·A·L·b （6）

其中，b为移动加速度。

在常应力σ_Z=N/A与结构尺寸不变的情况下，首先满足：

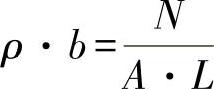
或者，在材料替代情况下，比例关系必须保持大小相同，即：

ρ·b=常数 （7）

下面的示例显示了这一结果。

示例：线性移动机械手

如练习图2-2所示，通过采用铝替代钢，机械手的加速度增大为

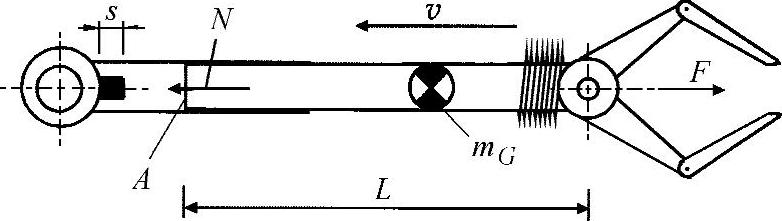
练习图2-2 机器人的机械手

这里，惯性力大小保持不变。

2.1.3 不稳定移动结构设计

举例来说，所有类型的机动车都属于这一类别。由于常常减速或者加速，机动车必须适应一定的节奏。如果放弃提高加速度，则减小设计重量可以取得显著的节能效果。这一点可以由下面的地铁案例加以证明。

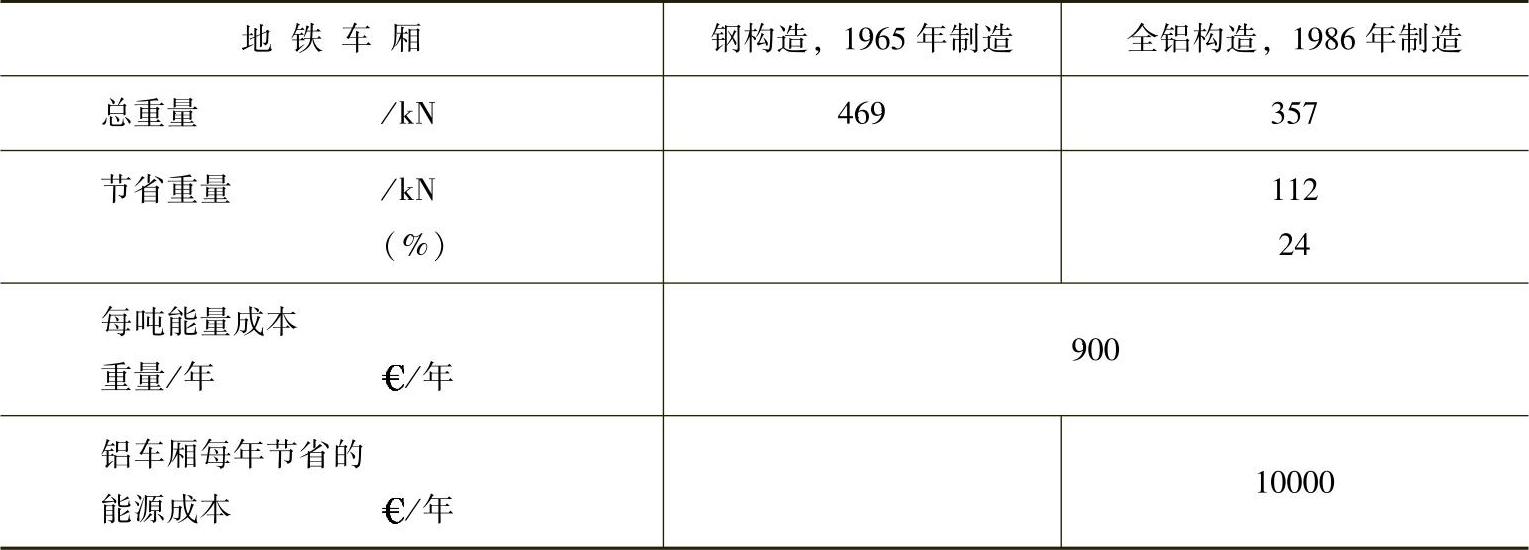
如果假设一列车由5节车厢组成，通过材料替代，每年最多可以节省下50000€的能源费用。

2.2 弹性模量的影响

如果一种材料的弹性模量小于钢的弹性模量，则在承载结构设计中要考虑到，由该材料制成的结构会产生更大的变形。在采用铝方案替代钢方案重新设计的时候，特别要注意到这一点。

2.2.1 刚度相同的参数选择

绝大多数情况下，承载结构要满足变形条件。由于铝的弹性模量只有钢的弹性模量的1/3，其变形则为钢的3倍。对于不同的应力载荷类型，这一点决定了必要的设计措施。

示例：拉应力载荷

如练习图2-3所示，在应变相同的情况下，采用铝的结构，则杆的横截面积要求为

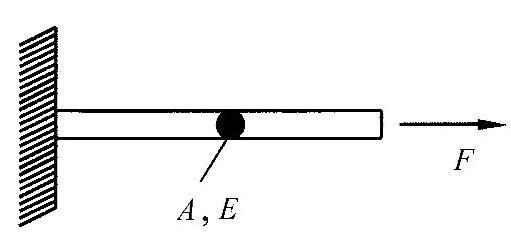
练习图2-3 拉杆

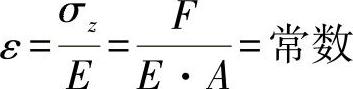
就是说，在给出的外力F下，分母必须保持为常数。由此，可以得出：

E_铝·A_铝=E_钢·A_钢

或者

从这里可以看出，在拉应力载荷设计中，由于钢的重量正好是铝的3倍，所以无法达到减重效果。

示例：弯曲应力载荷

如练习图2-4所示，对于抗弯梁的挠曲，可以根据载荷与支座情形加以计算：

练习图2-4 弯曲横梁

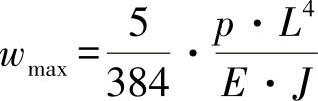
在钢梁和铝梁的挠曲相同的前提条件下，有：

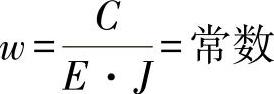
由此，可以得出相应的面积惯性矩为

E_铝·J_铝=E_钢·J_钢

或者

现在，是否能减轻重量取决于如何实现这一面积惯性矩。当横截面尺寸还可以更改的时候，就总是有重量可减；就是说，要在尽可能小的横截面面积上达到最大的面积惯性矩。在这种情况下发生弯曲，高度的变化最大。对于练习图2-5中所示的I-桁梁可以得出以下结果。

练习图2-5 抗弯刚度相近的钢抗弯梁和铝抗弯梁

作为补充，还应当采用位于中心的单一载荷考察一个平板的挠曲。

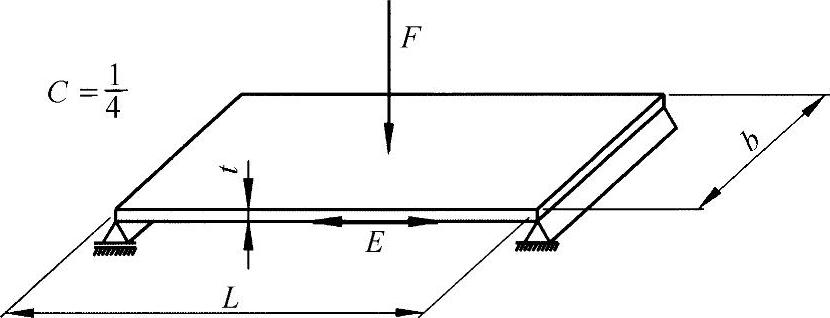
练习图2-6 单一载荷作用下的平板

如练习图2-6所示，这里，位于中心的挠曲为

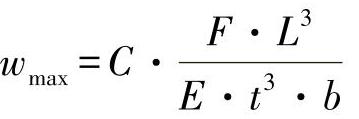
并且应保持为常数。C为考虑到支座条件新引进的一个常数。

在钢板和铝板的挠曲相同的条件下，可以由此得出平板的厚度为(www.xing528.com)

E_铝·t³_铝=E_钢·t³_钢

或者

如练习图2-7所示，如果能实现这一厚度比例关系，铝的结构可以比钢的结构减轻重量50%，如下表所示。

为了评估平板的刚度，这里可以采用比刚度作为典型的特征值。这可以由下面的步骤导出：

●由变形条件：

●由平板重量：

练习图2-7 刚度相同的钢平板和铝平板

当平板所有的构造尺寸都确定后，刚度值最大的平板就是最轻的板。

2.2.2 稳定性相同的参数选择

对于不稳定性的参数选择来说，如前面一样，结构设计的刚度起主要作用。

示例：压弯

如练习图2-8所示，按照欧拉公式，一个中心受压杆的弹性压弯载荷可计算为

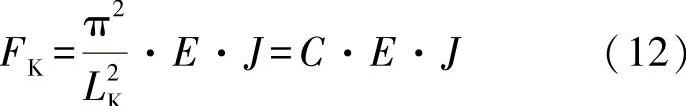
其中，。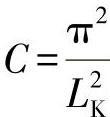

为此，对于压弯来说，须满足在弯曲时已经导入的比例关系。在相同的压弯安全性下，要求

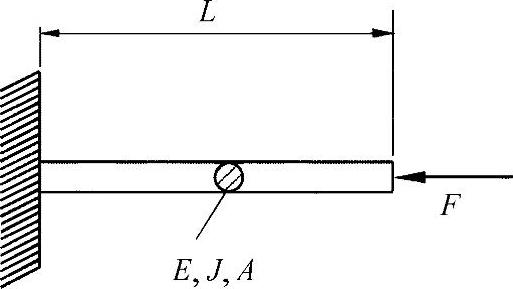
练习图2-8 抗弯杆

的面积惯性矩为

J_铝=3·J_钢（13）

其中，J≈2π·r_m³·t；G=μ·L·g。

这里，采用如下练习图2-9所示的圆杆进行了比较。结果表明，薄壁圆管的方案更好一些。

练习图2-9 压弯安全性相近的钢抗弯杆和铝抗弯杆

由此得出的结论是：当采用铝管替代钢管作为压弯支承时，在壁厚相同的情况下，直径比例关系须为

这意味着，直径增加44%。不过，分析也表明，当直径增大后，薄壁钢管的性能则更好了。

示例：凸起

如练习图2-10所示，如果在一个承受压应力载荷的盘上，超出了一定的临界应力，则在中心平面上会发生凸起。该临界应力可如下计算：

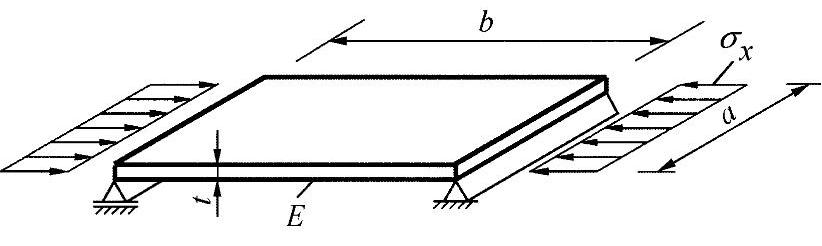
练习图2-10 受压盘

这里，k是与实际情形相关的凸起值，考虑到了支座、几何尺寸和应力载荷。

对于矩形场，凸起值为

其中，。

练习图2-11显示了在一个平放的盘上，凸起值对于不同大小的场的意义。

练习图2-11 盘的凸起值

为了达到与钢盘一样的凸起强度，可以将铝盘加厚，即：

尽管采取了这样的措施，采用铝材依然可以减轻重量42%，即有：

2.2.3 强度相同的参数选择

对于强度参数选择应当假设，材料直至屈服强度都是可以利用的。

示例：平板弯曲

如练习图2-12所示，固定的平板应通过一个位于中心的单一载荷受载，所允许的载荷可计算为

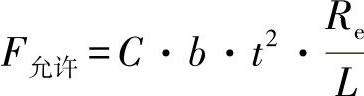
练习图2-12 平板弯曲

平板的重量为

G=m·g=ρ·g（b·L）·t

采用要求的板材厚度：

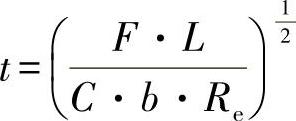
可以得出：

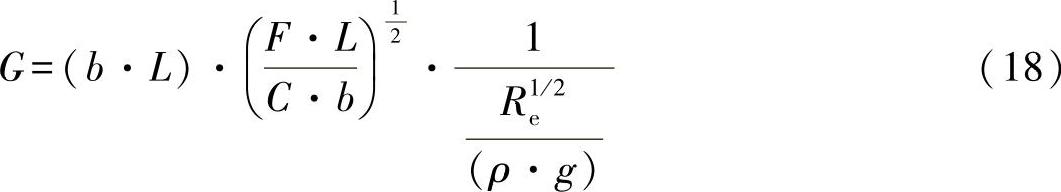
由此可以看出，通过最大的比特征值R_e¹/2/（ρ·g），可以得出最轻的平板。

2.3 变形能的影响

如练习图2-13所示，冲击应力载荷结构组件（如：挤压型材、冲击盒）就是一个典型的考虑到变形能力的设计结构。在这种情形下，由于具有较低的弹性模量，铝更适于作为这类结构的材料，因其在相同的力导入情形下会产生更大的变形。

变形功通常可如下计算：

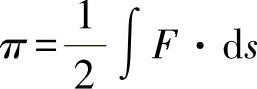
在线弹性区域有：

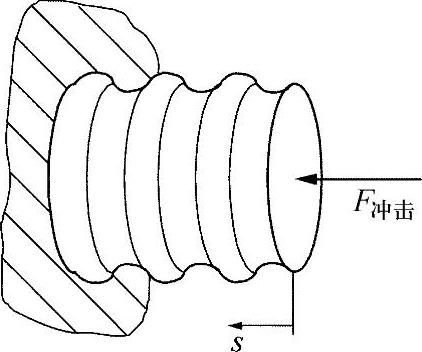
练习图2-13 冲击应力载荷型材

对于作用力，可进一步得出如下的内在关系：

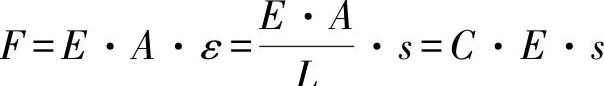
由该式可导出比例：

在能量吸收相同的情况下，变形比例为二次幂：

对于内力则有：

在基本强度大致相同的情况下，采用铝材料可以具有更大的抵抗塑性变形的储备能力。

在汽车制造中，越来越多地采用铝合金型材替代钢纵梁承受冲击载荷。在汽车工业中，用于承受拉压应力载荷的结构件替代的壁厚经验计算公式为：

其中R_m表示抗拉强度；A表示伸长率。

如下所示为替代方案可能性的参考图。

铝与参考材料相比较没有重量优势。不锈钢倒是具有重量上的优势，在实际中也得到了越来越多的应用。