固体声传播特征速度与频率弥散

在固体中，激发以特征速度进行传播。在这种情况下，不仅是弹性轴向变形会遇到阻力，剪切变形、弯曲变形与扭转变形也会遇到阻力。因此，在固体中会出现轴向波、切向波、弯曲波与扭转波。

●延伸波

延伸波可表示为准纵波（轴向波）。对于钢（ρ=7850kg/m³，E=2.1×10¹¹ N/m²）来说，可确定其传播速度亦即延伸波速度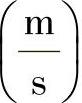为：

延伸波（图26-2）产生的前提是，物体横向的尺寸小于波长。通常在杆形结构中存在这样的比例关系。

带有二次横波的准纵波也会出现在平板形的结构中，即出现在平板表面上。对于钢（ν=0.3）来说，平板中的延伸波速度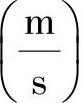为

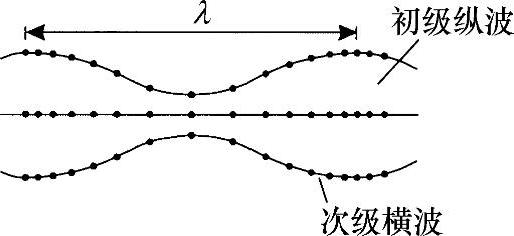
图26-2 延伸波原理[HEN 01]

●密度波

如果固体在所有三个方向上的空间膨胀大于产生的波长，则在轴向激发上会产生纯轴向波或者膨胀波（密度波）。传播速度具有球的形状。因此，可计算密度波速度为

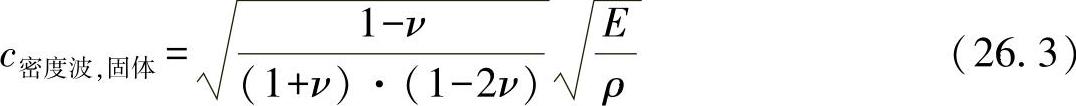
由钢材构成的固体，其密度波速度c_{密度波，固体}=5970m/s，比杆状结构中的传播速度高15%。在图26-3中，这一过程以抽象的形式表示出来。

●切向波

在空间结构中，由剪切力激发可引起纯横向切向波。切向波以空间的形状传播。在钢材（G=8.1×10¹⁰N/m²）中，切向波速度为

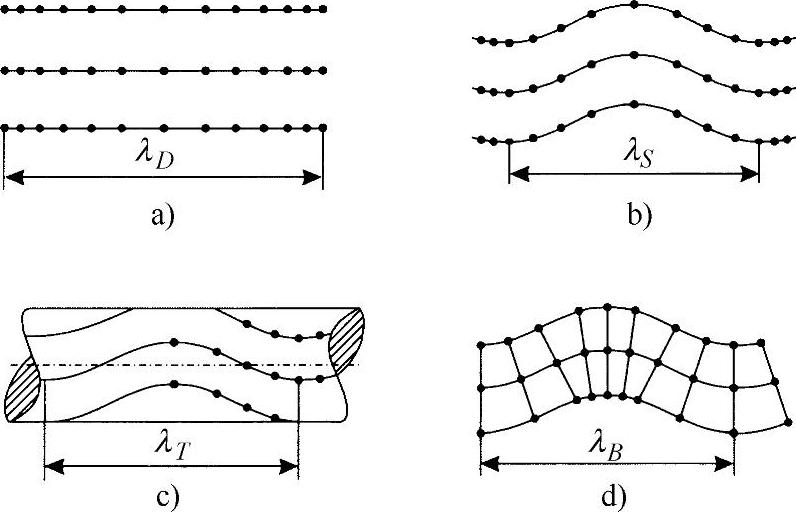
图26-3 结构中的波传播[HEN 01]

a）密度波 b）切向波 c）扭转波 d）弯曲波

●扭转波

切向波的一个特殊情形为在杆状固体中的扭转波，其表现形式为圆周形状。扭转波的速度为

式中，G·J_T为扭转刚度；Θ_x为围绕纵轴的质量惯性矩。

在圆形结构横截面情形下，c_T=c_Q。(www.xing528.com)

●弯曲波

轻量化结构承受最多的是弯曲应力载荷，因此，弯曲波对于固体声的传播和辐射是最重要的。在所有固体横截面同时倾斜的情形下，弯曲波会产生横向偏移。

在杆状固体中，自由弯曲波的传播速度为

式中，J_b为面积惯性矩；μ_L为单位长度的质量；f为激发频率。

式中，i为惯性半径。

对平板进行类推有：

式中，μ_A=ρ·t≡每个面积的质量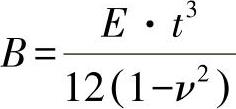；，为抗弯刚度。

与

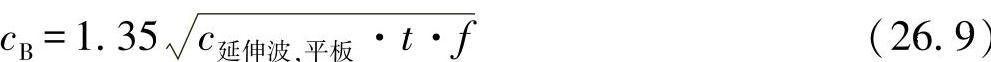
因此，可确定一个弯曲波的波长为

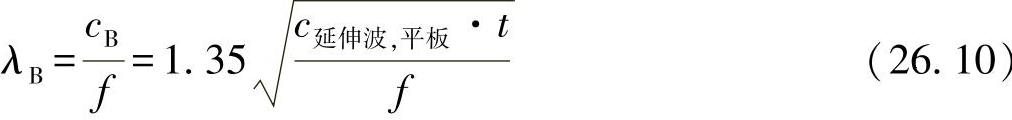
与迄今为止所得到的波传播速度不同，弯曲波速度取决于频率f，并且随着频率的增加而增大。这一现象被称为固体声的频率弥散。

与应力载荷相对应，所有的构造波形状都会在固体中出现，也有可能发生波转移。例如，当延伸波在角或者节点处被反射回来时，就会变成弯曲波。

●易弯固体的横向波

预紧易弯固体（钢丝、琴弦）在振动下会产生横向波（图26-4）。

对于延伸波速度，在式（26.1）中，用预应力替代弹性模量，可得出：

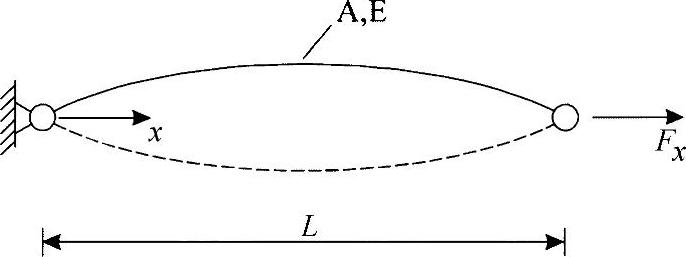
图26-4 在弯曲松弛、杆状物体上的第一横波[HEN 01]

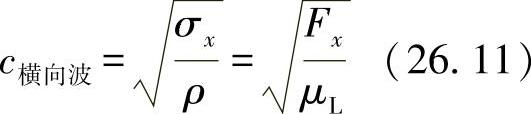
如前面已经确定的，在围绕声音的介质中，只有垂直于表面的相对运动是声音辐射产生的原因。这取决于在延伸波很小的范围内和在弯曲波很强的情况下，横波是以什么样的方式出现的。这里，弯曲波是非常关键的。