早期失效和后期失效-轻量化设计、计算基础与构件结构

在一个由很多彼此相互连接的单一部件组成的结构中，会存在摩擦或者其他的系统因素的作用。实际中，可由早期失效、随机失效与/或后期失效来加以确定。图25-1中采用失效曲线（浴盆曲线，见[AUT 84]）对失效行为加以描述。

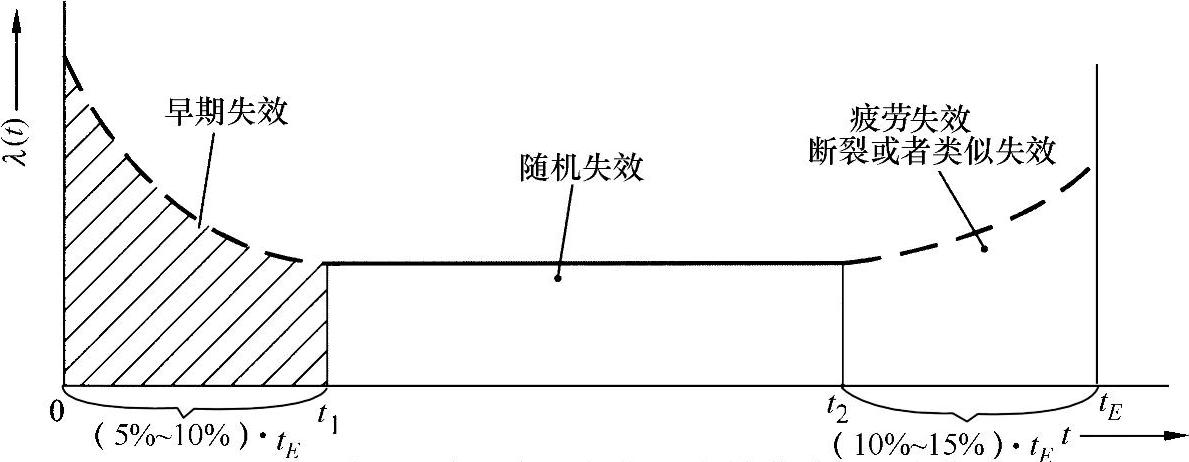
图25-1 根据不同区域而变化的失效曲线（浴盆曲线）

这里，可以将曲线划分为三个区域：

●在间隔t=0到t₁内，故障率曲线下降。早期失效的特征是由原厂缺陷（加工缺陷、装配缺陷或者材料缺陷）引起的。

●在间隔t₁到t₂内，故障率稳定，因为之前所有有缺陷的结构都已经失效了。进一步的失效只是偶尔发生。

●在间隔t>t₂后，故障率又重新上升，其原因可能有磨损、老化或者疲劳。

上面所描述的行为，在数学上可采用魏布尔分布[BER 86]加以描述。就是说，对于上述失效行为，可采用两参数或者三参数的魏布尔分布进行计算。

●对于两参数的魏布尔函数，对应的幸存概率：

其中，t为时间变量；T为特征寿命（在63.2%失效下）；b为控制分布曲线形状的形状参数。从b=3.44开始，魏布尔分布大约对应于高斯分布。

密度函数可计算为

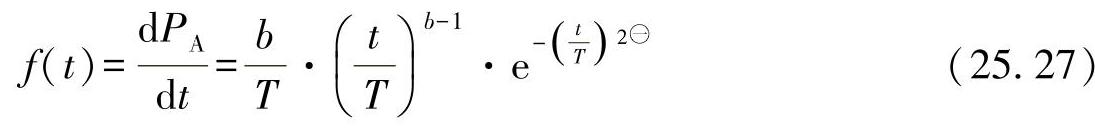
㊀对于P_A=1-e-（t/T）b与t=T=1，有P_A（T）=0.632，并且与b无关，因为有1^b=1。由此T描述了直至所有结构/系统的63.2%都发生失效的寿命。

故障率为(www.xing528.com)

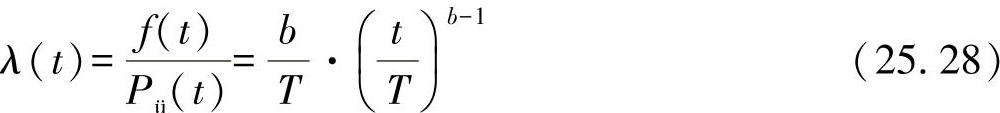
经验表明，用两参数魏布尔函数计算出的寿命几乎总是低于实际测出的寿命。其原因可能是，根据方程式（25.26），假设在时间点t=0已经发生失效了。不过，这在实际情况中非常罕见。通常可以假设，每个结构都有一定的最低寿命，只有超过了最低寿命后，失效才会发生。

●对于三参数魏布尔函数，通过一个附加的参数t_o将无故障时间考虑进来，则有：

总体来说，该方程对工作行为描述的效果更好一些。

对于密度函数，可有：

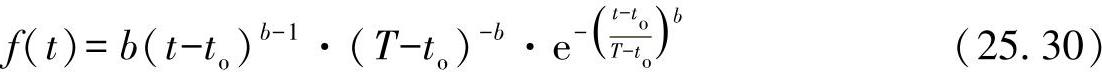
并且有故障率：

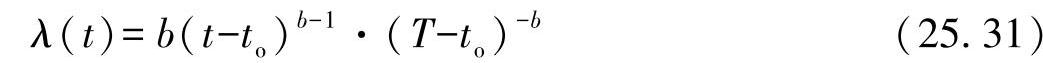
实际中，对t_o的确定意味着要进行大量的试验，所以通常对其进行估算。通常将早期失效的三分之一假设为无故障时间，采用这一假设，有：

其中，t_E表示寿命结束估计值。

按照目前的知识水平，迄今为止，在预测结构的寿命方面，还没有比魏布尔函数更可靠的方程式。