进一步可假设,一个结构是由带有不同薄弱环节的多个元件组成的。对于单个元件来说,通过仿真或者试验研究,其幸存概率或者失效概率可以是已知的。现在需要预测的是,单个薄弱环节对整个结构会有什么影响。
根据一般性知识可知,在一个技术体系中恒定有确定的布尔基本排列。该布尔基本排列或者为串联排列,或者为并联排列。
在布尔基本排列中,从拉普拉斯意义上可将失效或者幸存看做是互补事件。因此,对于一个结构/系统有:
Pü+PA=1 (25.1)
对单一的薄弱环节/构件有:
Püi+Pai=1 (25.2)
由此,可如下表征基本排列:
●串联排列:这种情形可表示为,关键元件(K1~Kn)一个跟着一个地作用。在这种情况下,只有所有的元件都幸存下来,一个结构才能幸存。因此,结构的幸存概率为
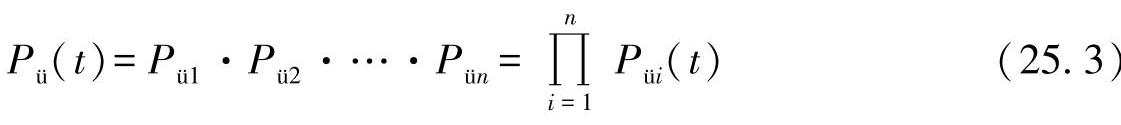
或者失效概率为
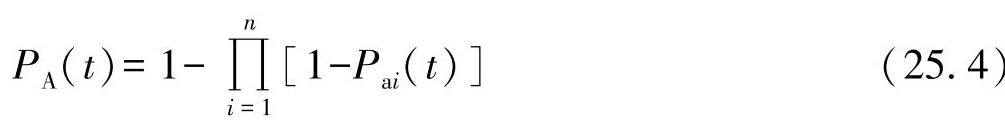
如果所有元件呈现相同的概率值,则上述方程可以简化为指数律:
Pü(t)=Pnüi
PA(t)=1-(1-Pai)n (25.5)
●并联排列:这种情形由分叉标识,即存在多个力的路径。一个元件的失效不会导致整个结构的失效。结构失效概率为(https://www.xing528.com)
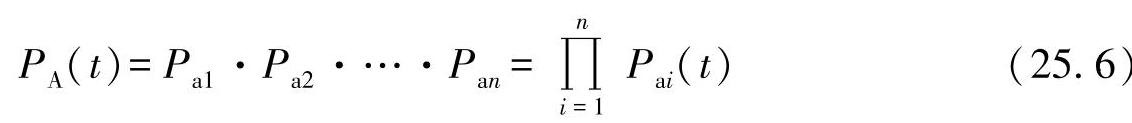
或者幸存概率为
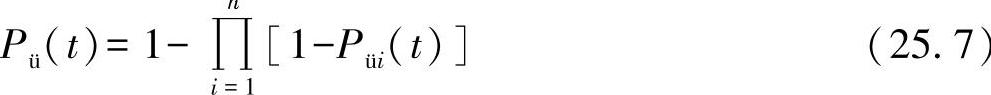
如果所有的概率相同,则可形成如方程式(25.5)所示的双元关系。
在表25-1中,用符号表示了典型基本排列的构造。
表25-1 在可靠性框图中的逻辑基本排列[LEC 79]

在工艺体系中,到处都有串联排列,力的变化过程通过所有的构件传递,最后达到一个平衡状态。一般情况下,大多都是这样的排列。在并联排列中,力的变化被分解了。实际中这样的情况相对比较少,尽管也有一些实用案例(如载货汽车的双回路制动系统、燃油箱的双层壁等)。
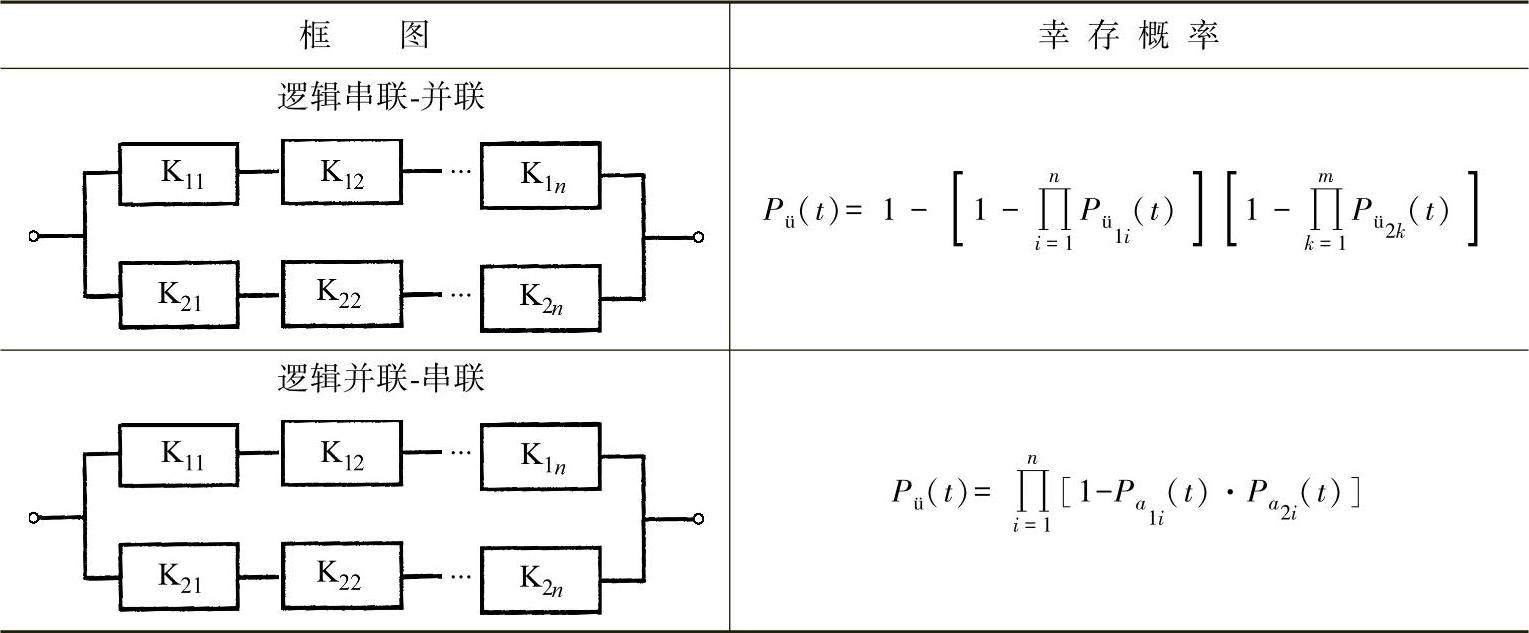
另外,也经常会出现这两种基本结构的混合排列。表25-2所示为并联-串联排列的构造形式。
当正好有两个在相对支路上的元件K1i、K2i产生失效时,串联-并联排列失效。不过,发生这种情况的概率非常小。并联-串联排列方式则可提供更高的可靠性,因为这里的每个环节都有冗余度。只有当一个并联排列整体失效时,才会发生结构的总体失效。
在表25-2中,示范性地列出了属于这种排列的概率函数。
表25-2 混合排列的可靠性框图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




