轻量化设计：非线性损伤假定

在前面介绍的线性损伤累积中，可用单一损伤系数简单相加来评估寿命。这里并没有考虑到实际的载荷变化过程。从这一点来看，采用这种方法得出的结果只能用来进行非常粗略的评估，而且实际上只适用于方案比较。只有考虑到顺序效应（根据经验，低-高载荷不如高-低载荷那么关键）以及载荷相关的材料损伤，评估才可能更准确。近几年来，研究人员集中开发非线性损伤假定方法，在这种情况下，假定一个行为，如图24-15中所示。

在上述描述中，理论的线性损伤可以表示为图中的对角线，而曲线表示的是实际的损伤。对于一个轻量化构件来说，如果承受有限的、单级振动应力载荷，则损伤分量为

在这之后运行的损伤机制可以从数学与物理角度来加以解释。举例来说，对于一个Miner假设等效的3级集，可计算为

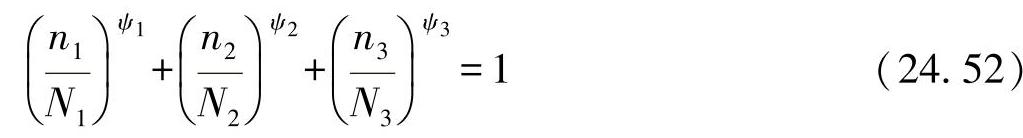
并按照累积法则进行转换：

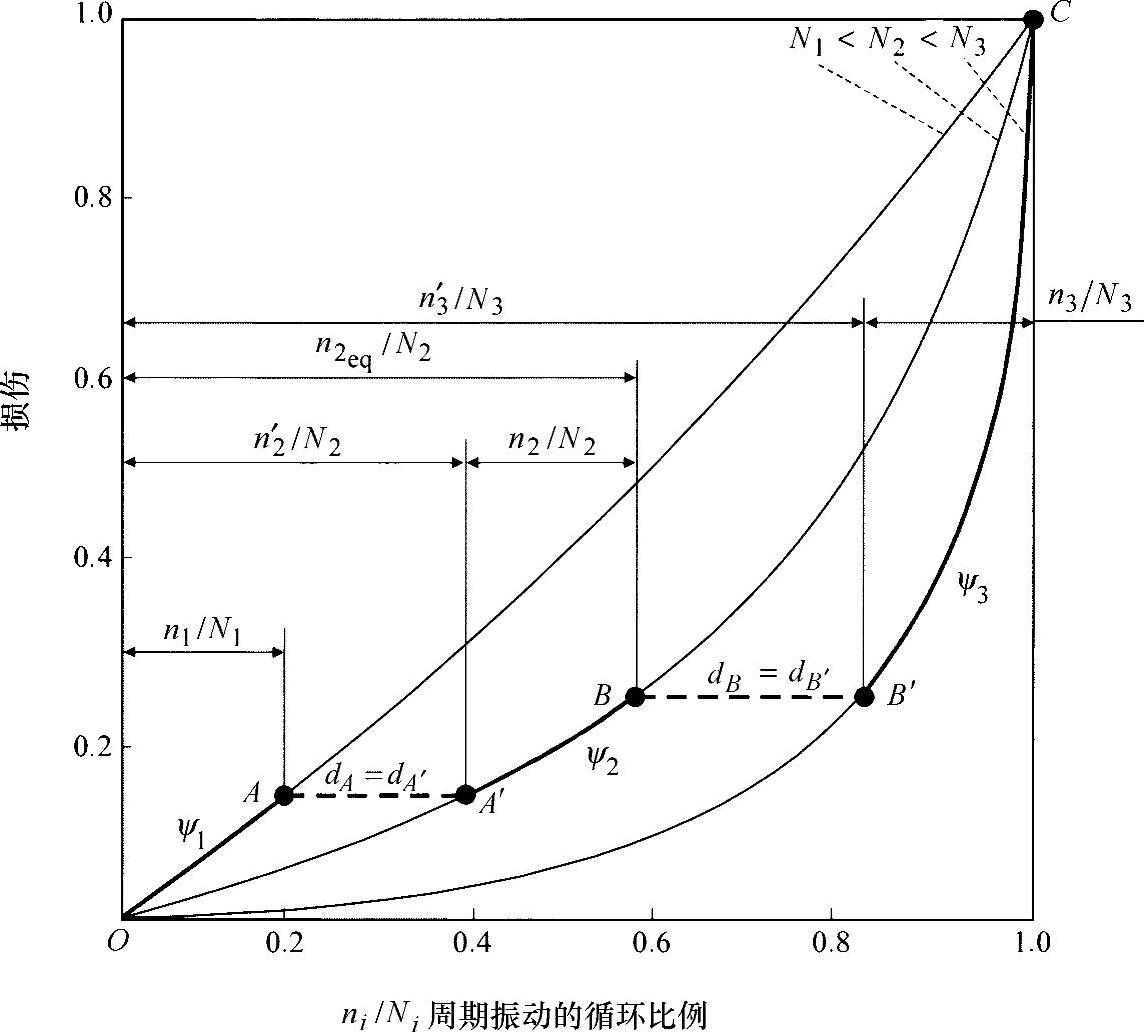
图24-15 在三个集层级上的非线性损伤过程

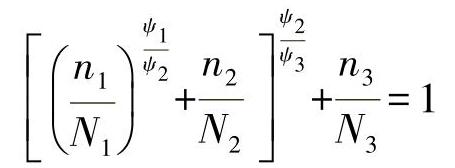
从物理学角度上看，这个过程复杂一些，可进行如下推导：

●在进入第一级时，对于一个高的载荷水平σ_a1、n₁，可通过路径OA得出载荷循环，直至断裂载荷循环次数N₁，载荷是可承受的。但是，在n₁范围内只产生了部分损伤d_A（直至状态A）。

●在转换到较低的载荷级σ_a2时，因为存在另外一种损伤行为，则必须从状态A变换到状态A′（新的初始状态）。

●为了用一个较低的载荷水平σ_a2通过载荷路径OA′生成相等的部分损伤d_A′（如d_A），（虚构的）n₂′应承受振动循环。用这个重要的损伤参数可以列出如下方程式：

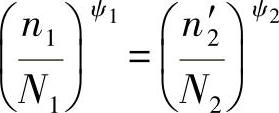
或者（24.53）

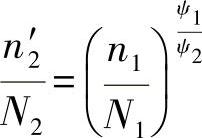
●在B的第二个载荷级的终端，可设置一个等效周期数n_2等效，根据下式相加：

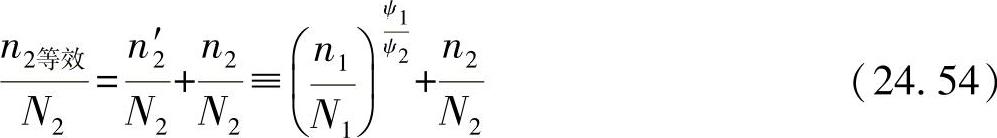
该式由变换分量和实际分量组成，可重新得出相对部分损伤d_B。

●现在考虑到前面的等效周期数^[9]，则从下一个载荷级σ_a3、n₃直到最后在C（D=1）的失效可作为一个二级方程式推导出来，即有：

替代上面的关系，可得出一个三级应力载荷：

(www.xing528.com)

下一步的目标须为，将该方程式通过i应力载荷级加以推广：

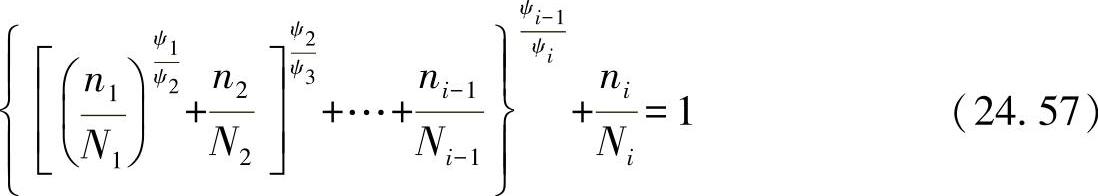
近年来，开发出了一些针对这个非线性原理的损伤理论（如Subramanyan，Hashin，Manson/Halford），这些理论的本质区别在于，作者如何计算损伤参数ψ_i。所有作者都采用沃勒线作为基准，考虑到这些方法具备更好的实用性，须将其加以分类。

在试验中得到了最好证明的是Manson方程[MAN 81]。按照Manson方法，损伤参数可计算为

ψ_i=N^P_i （24.58）

对于钢来说，重要的系数位于区域p=0.3～0.5（均值：p=0.4）。由此得出的损伤法则为

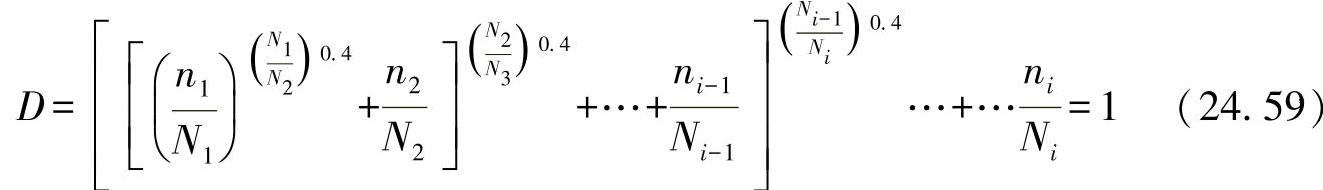
适当地对该方程进行叠加：

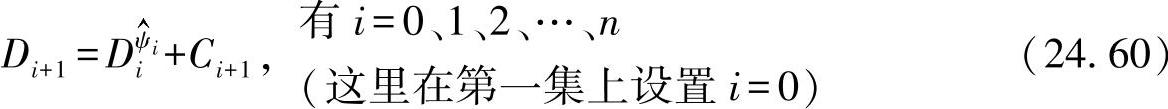
考虑到：

D_o=0

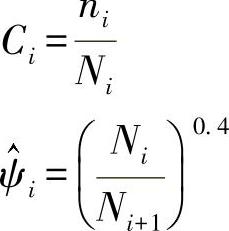
最后得出损伤和D_n。在一般情况下来看，与实际达到的使用寿命相比较，这种方法预测的结果非常好（由650个试验得出的结果）。

[1]如果想保留这个信息，就必须过渡到多维计数（如：雨流体）。

[2]对于磨损问题可回溯到相对应的魏布尔分布。

[3]“针对钢件、铸钢件与灰铸铁件沃勒线的计算—合成沃勒线”，ABF 11报告，德国冶金业者协会，杜塞尔多夫1984。

[4]试验表明，线性比例的假设并没有得到证实，而是出现了非线性关系。

[5]在Miner所进行的试样试验中，在DK_min=0.79与DK_max=1.49之间确定了损伤和。Miner试验结果的平均值为D_K≈1.05。

[6]特别突出的测量值必须进行异常测值测试（如：按照Pearson或者Grubbs方法进行测试）。

[7]在美国ASTM标准中b≡W（宽度）。

[8]裂纹的生长速度可为da/dt，采用测试技术通常无法得到其值。

[9]上面的写法与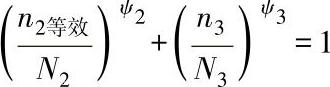一致。