基于断裂力学的轻量化设计计算与评估

继续进行前面的研究，则现在应当考虑阶段周期性振动应力载荷。迄今为止，与裂纹生长行为相关的现象还没有完全解释清楚。下面从注重实际出发，介绍断裂力学累积，出发点为图24-14中所示的阶梯集。

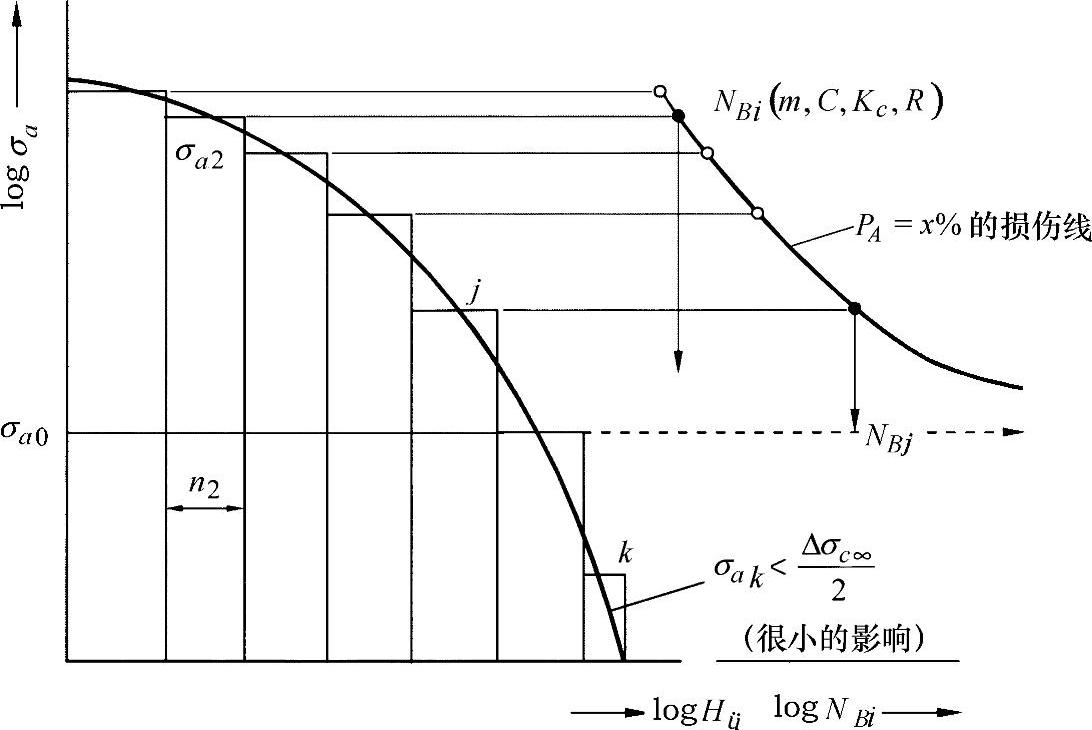
图24-14 裂纹集与断裂力学损伤线，对于m、C的失效概率P_A=x%

考虑到断裂力学的疲劳强度值ΔK_o，将载荷集限制在有效的裂纹集上。对裂纹生长起决定作用的只有应力振幅：

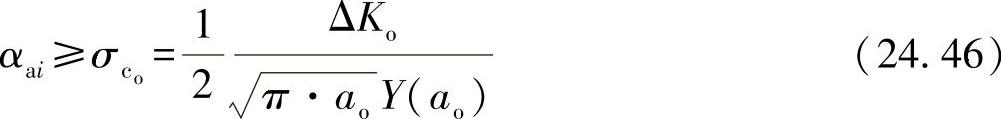
小的振幅由于不会导致超出极限值，对裂纹生长没有影响或者影响很小。（这样的约束条件是很普遍的，由此表示了Palmgren/Miner假设的一个类推。在这种情形下，随着材料塑性的不断增加，须取消这样的约束。）

在等效单级应力载荷的假设下，现在可应用裂纹生长法则来确定对于所有级的损伤线。这里可以采用Paris方程或者Forman方程。其过程设计如下：

●对Paris方程一级一级地积分

在方程式（24.42）中，可给出用于叠加载荷循环次数评估的内在关系为

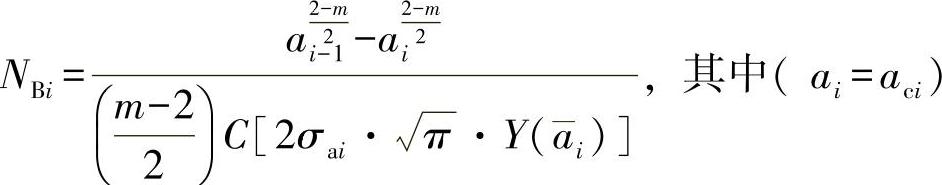
叠加区域包括σ_ai到a_ci的应力水平。与水平相关的临界裂纹长度a_ci须采用超出计算加以确定，也即在a_i=a_ci下，由不等式：

(www.xing528.com)

加以满足。

在得到所有重要的损伤N_Bi值后，可以进行类推断裂力学损伤评估。在每级上都可得出一个损伤分量为

●对Forman方程一级一级地积分

Paris方程只能覆盖平均区域，而Forman方程则由图24-14可用其角值（ΔK_o，ΔK_Ic）得到整个裂纹生长变化过程。从这一点来说，一级一级地确定断裂载荷循环次数N_Bi的准确性较高一些。如果在分析问题中有这样的要求，那么，为了评估载荷循环数，则要引入方程式（24.45）。否则的话，可如前面所述来设计计算过程。

如同传统的损伤计算一样，现在可计算断裂力学累积：

受这样一个集冲击的构件，其总的使用寿命为

该式表示了一个集重复因子，覆盖了三个阶段，晶粒破坏➝裂纹➝断裂。