残余强度评估与构件设计

如果在出现裂纹后，有可能会产生结构性失效，则如今在安全考虑下，要求进行损伤允差验算。该验算要求回答以下问题：

●一个开裂构件的残余承载能力有多大？

●能否通过取消应力载荷来延长服务期限？

●裂纹在构件中如何扩展？

从这一效果的可计算性考虑，可以采用线弹性应力强度的断裂力学概念（K概念）。在这一概念的基本形式中，首先描述了静态的情形。为了进一步分类，须定义出图24-10中所示的应力载荷情形（Modi），它表征了裂纹张开行为。

这里，最关键的振荡类型是I，裂纹垂直于裂纹端口（脆性断裂）张开。应力变化过程可根据Williams-Irwin方程进行计算：

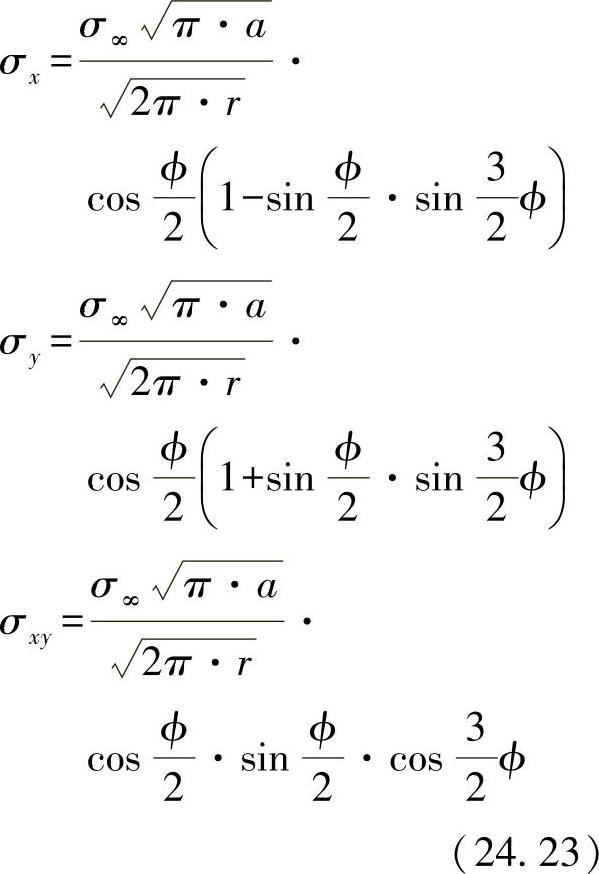
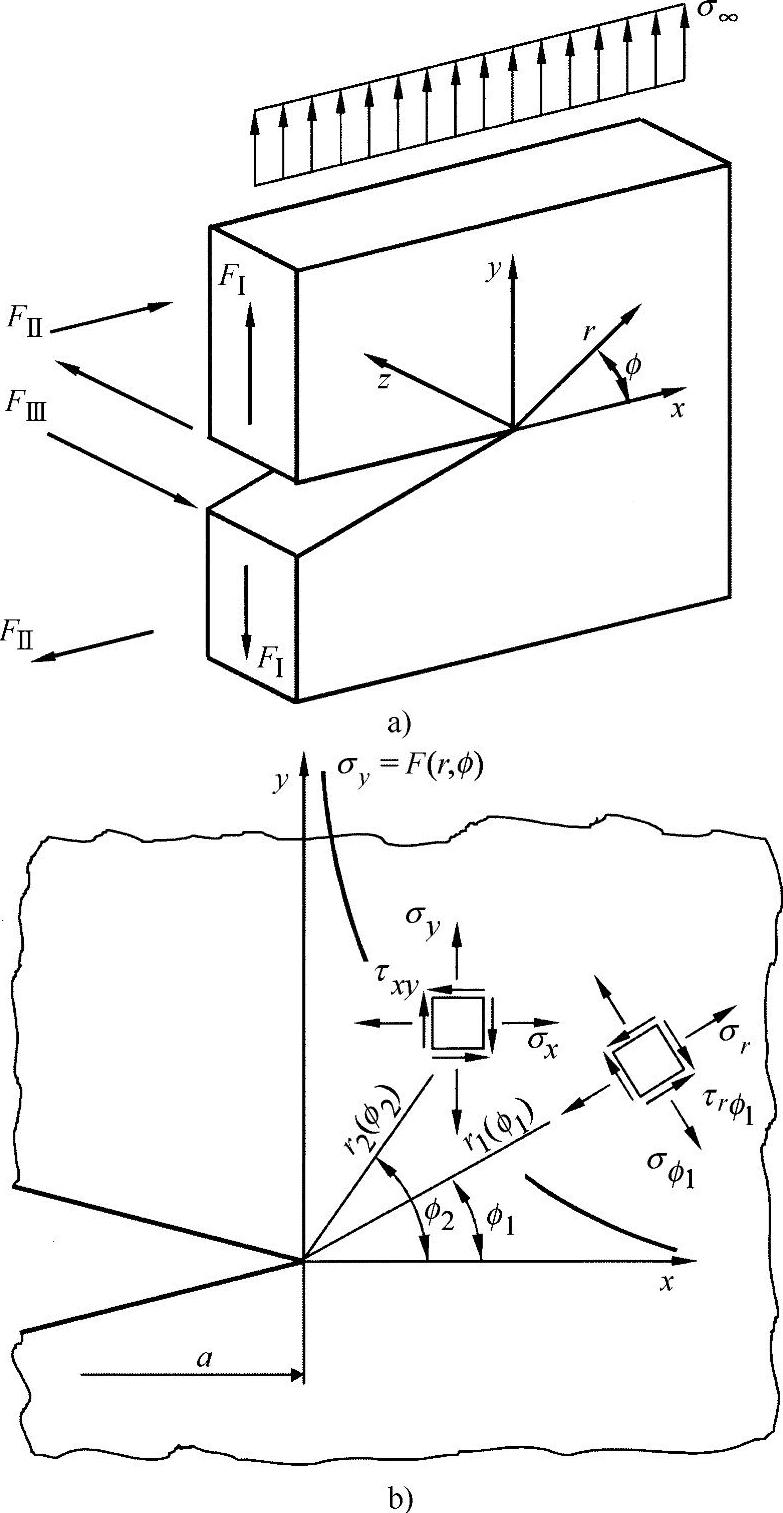
图24-10 裂纹张开类型与裂纹峰值上的应力变化过程[SCH 80]

（Ⅰ=法向力振荡类型，Ⅱ=纵向剪切振荡类型，Ⅲ=横向剪切振荡类型）

如果在最大程度上与是否存在内部裂纹或者外部裂纹无关，则对于方程式（24.23）来说，总是存在类似的函数，以使得上面的方程在用于计算时普遍有效。但在由脆性材料构成的无限盘中，对于裂纹的有效性有着严格的限制。

在给出的外应力载荷σ∞与出现的裂纹a下，方程式（24.23）中的分子是一个恒定参数，该分子只是按比例放大通过分母确定的应力变化过程。由于按照这种方法，在裂纹峰值的应力状态强度可以得到控制，则可将分子表示为应力强度因子：

对于带有各种裂纹形状的实际构件来说，可以通过一个修正函数来配合对于无限盘的有效关系：

绝大多数裂纹的修正函数Y（a）（表24-1）都可列表得出。产生的缺陷类型总是可以归类于这些裂纹的几何形状种类。与此相关，可推导出下列判断：在不同的构件中，如果应力强度（即其振幅宽度）的值相同，则会产生相同的残余强度与裂纹生长行为。据此，可将由试验得出的行为样本直接用于构件上。

表24-1 各种裂纹几何形状的修正函数[HAN 86]

（续）

按照静态断裂准则可以看出，在达到应力强度因子的临界值时，一个原来静止的裂纹（裂纹导入）开始了不稳定的裂纹扩展。

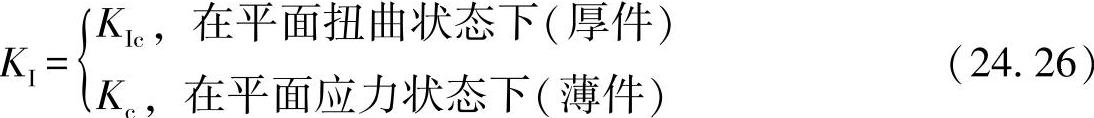
该临界值用裂纹断裂韧性来表示。在用这一标准进行评估时，必须要区分出厚壁件（平面扭曲状态下→K_Ic）与薄壁件（平面应力状态下→K_c）的不同。在此种情况下，这里引入的裂纹韧性K_Ic是一个材料常数（采用CT试样求得），通常可从表中将其查出来。

如下的数据可作为依据[AUT 79]给出：

●建筑钢K_Ic≈2000～4000Nmm^-3/2

●调质钢K_Ic≈700～2500Nmm^-3/2

●渗碳钢K_Ic≈2000～5000Nmm^-3/2

●铝合金K_Ic≈800～1500Nmm^-3/2

●镁合金K_Ic≈1000Nmm^-3/2

●钛合金K_Ic≈2200～4500Nmm^-3/2

裂纹断裂韧性K_c为一个变量参数，从本质上说与构件的厚度和材料有关。因此，给出的K_Ic值位于裂纹断裂韧性的极限之下。(www.xing528.com)

现在，残余强度问题由以下的评估作为平衡条件：

σ_∞≤σ_c

这里σ_c表示了在总横截面上相关的临界失效应力。

考虑到方程式（24.25）与式（24.26），可计算有：

●对于脆性材料行为：

其中，a₀作为起始裂纹长度。

其标识为，不会导致稳定的裂纹扩展，并且有a_o≈a_c。在平面挠曲状态下，厚壁件（t>25mm）表现出了类似的行为。

●对于塑性材料行为：

其中，a_c作为临界裂纹长度。

因为绝大多数情况下，K_c值不是已知的，因此常用方程式（24.28）来近似求解：

为了在这一关系中能够对厚壁件加以分析和判断，对K_c值进行评估是非常重要的。可以从下面的图24-11中所示的试样出发，并测出裂纹阻力曲线。

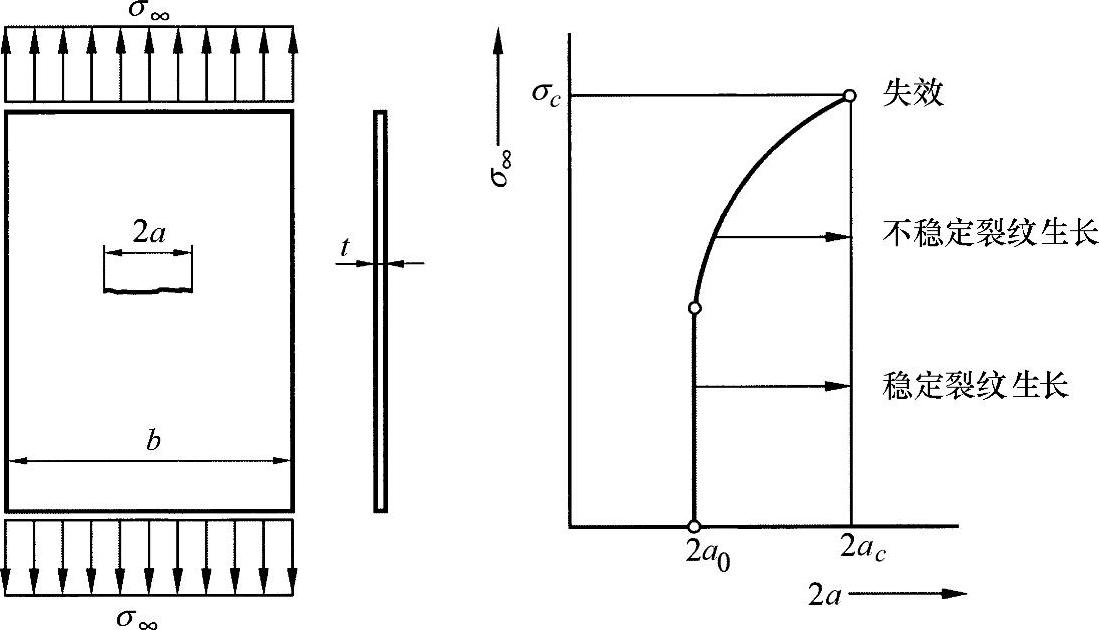
图24-11 薄壁件的CCT试样

为了减少测试消耗，只确定虚构的裂纹断裂韧性K_co=K_co（σ_c，a_o），用来替代准确的裂纹韧性K_c。试样的失效应力σ_c同样可以加以简化，即在2a_o=b/3^[7]下进行测量，并通过考察临界裂纹长度得出。由此，可给出虚构的裂纹韧性为

这里的前提条件是，试样的厚度与宽度与构件的厚度与宽度近似。

进一步考虑到Feddersen关系，可将方程式（24.29）如下传递到构件上：

其中

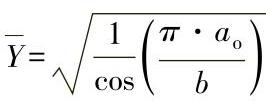
在这里，方程的适用领域受到下列限制：

●构件厚度，；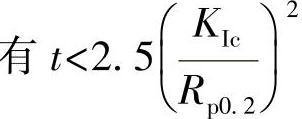

●构件宽度，；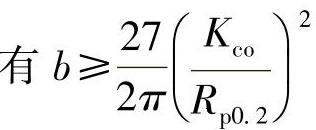

●失效应力，。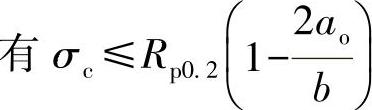

另外，由：

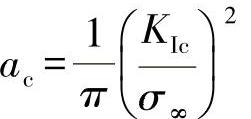
可以得出，临界裂纹长度也是有意义的。