机械做功损伤累积：深入探讨轻量化设计与构件结构

至此，本章介绍了如何求得构件的应力载荷与应力载荷性能。下面要对使用寿命进行量化。根据前面假设的限制，可以对直至裂纹形成的损伤累积有一个评估（时间、载荷循环）。这里，采用构件直至发生损伤时所吸收的功来求解构件的使用寿命。使用寿命与载荷范围的确定密切相关。由此引导出的问题包括：

●在规定的使用寿命内，对出现的工作应力载荷的可承受性；

●设计方案的使用寿命值；

●不同应力载荷过程的使用寿命值。

下面介绍的是几种常用的验算方法，即Palmgren-Miner累积法以及Haibach与Elementar-Miner-Regel修正法。

Palmgren-Miner法的假设基于在损伤和作用的振动循环之间的线性关系。这里假设，完成的损伤功与应力幅值和载荷循环次数^[4]大致成比例关系。这可在下面的模型中加以验证。

●采用试样进行寿命试验，可大致得到下面的关系：

就是说，对于所有的水平，损伤功/断裂功π₁=π_i=π_r=π相等，前提条件是恒定的单级应力载荷。

●现在假设一个等效集。为了便于比较，须将集从级1到级r分开。在每个水平上都有载荷循环n_i<N_i。有鉴于此，只完成了部分损伤功。其关系为

进一步假设，获得的集会导致断裂，则部分损伤功之和应当等于断裂功：

●由这一思路可有线性比例关系：

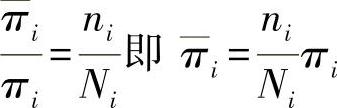
如将这一关系代入方程式（24.7），可得出断裂功：

或者

因此，对由于断裂造成的构件失效，载荷循环系数之和等于1即为Palmgren-Miner假设。通常对于一个任意集的系数和可给出为

根据定义可知，对于试样，D_K=1则产生断裂；对更大的构件来说，则意味着开裂。不过，对于高度安全件来说，通常需要将极限降低到D_K≈0.3～0.5，因为试验表明，围绕失效标准有一个离散区域^[5]。

图24-7所示为Palmgren-Miner方法实际过程的图形概念与计算概念，其结果由在沃勒线上集的镜像及其评估得出。

针对集的离散化，应形成至少8个层级，以使集形成相应的阶梯形（如：按照FKM准则）。

●Miner整理得出的条件是，所有集的应力载荷振幅应当高于疲劳强度。但在实际应用该方法时，往往却并不考虑这一点。这样一来，集只是反射到层级l，就是说，在这种情形下，无法得到m和n。由此可得使用寿命为(www.xing528.com)

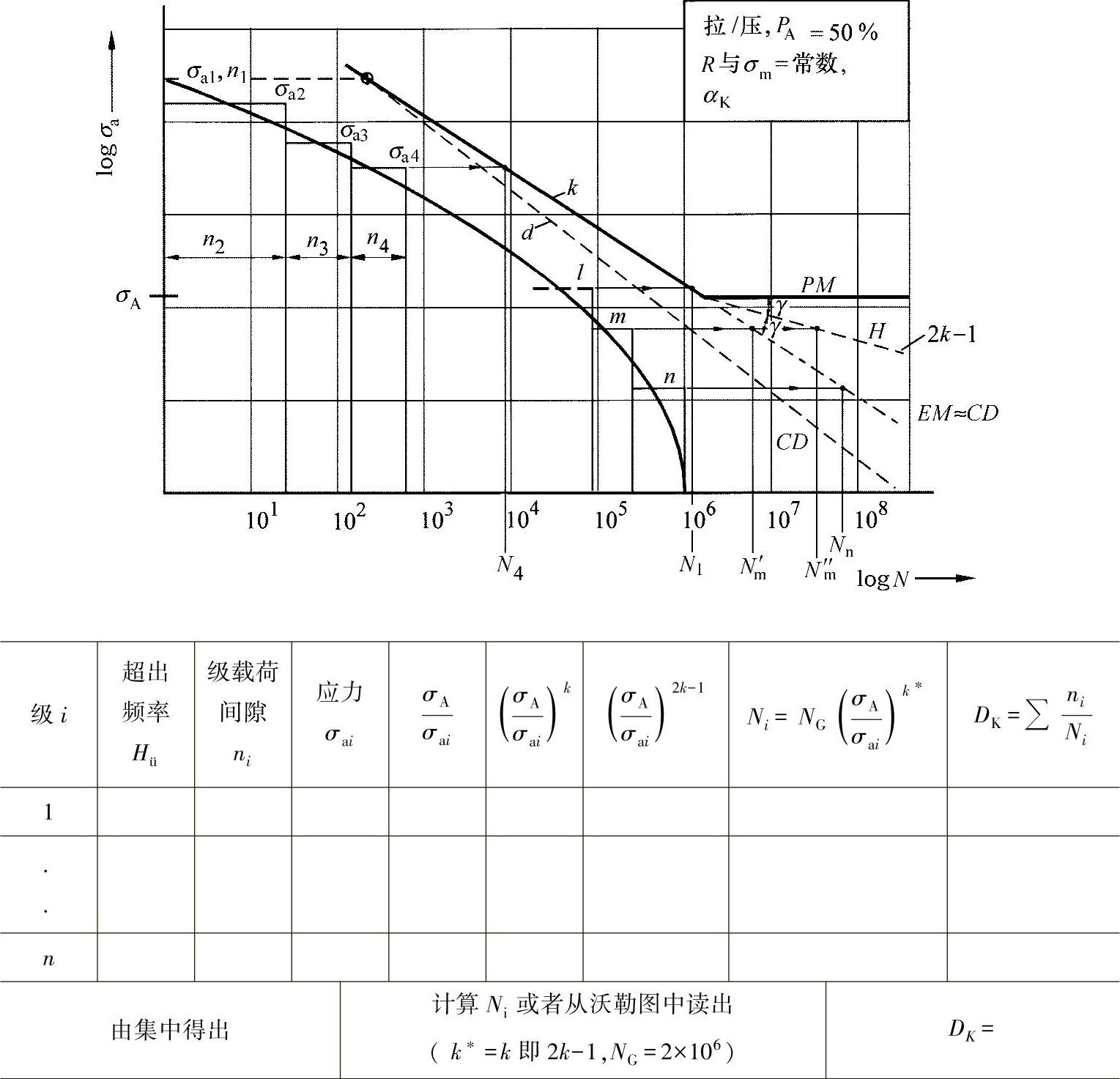
图24-7 损伤累积[Palmgren-Miner，Haibach Elementar-Miner-Regel/Corten-Dolan]

或者利用双对数沃勒线角值（σ_A、N_G）的关系，可得：

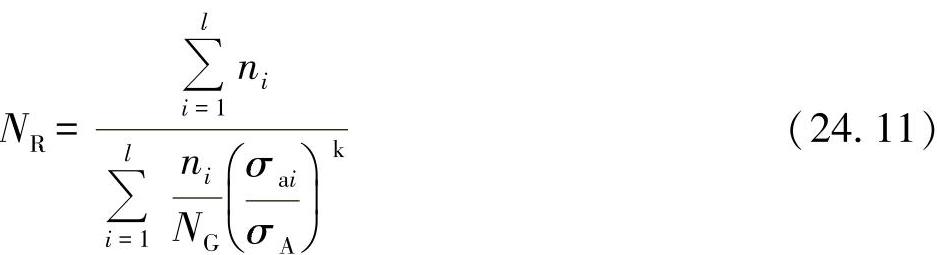
●在此之前，当在持久强度区域受到损伤时，位于疲劳强度之下的应力载荷振幅也造成了一定程度的材料损伤。正是基于这一认识，研究人员对Miner法进行了修正。Haibach和Elementar-Miner-Regel发现了Miner修正方法对实际应用的意义。在美国则主要是采用Corten-Dolan法，该方法如Elementar-Miner-Regel法则一样，原则上可适用于很多材料。为得到准确的方程，这里采用对持久强度分支的修正，即增加d=w·k≈k来加以处理。

按照Elementar-Miner-Regel法，要求持久强度分支在疲劳强度区域有相同的增长，这使得所有集级的镜像成为可能，对于损伤，则有：

对使用寿命则有：

根据Haibach的修正方程，在双对数图中，只要求持久强度分支在疲劳强度区域中有一半的增长。由此，可得出部分损伤和为

其中，

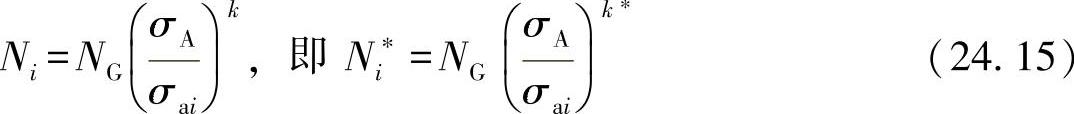
与

k^*=2k-1 （24.16）

则又可得出使用寿命为

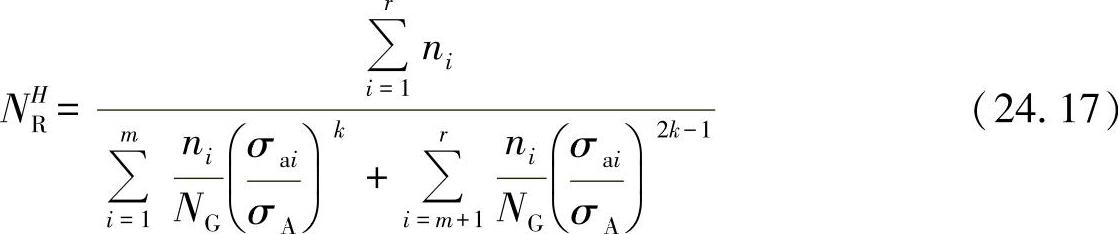
与试样的结果进行比较表明，按照Palmgren-Miner方法计算的结果大多过好，而按照Elementar-Miner-Regel计算的结果又大多过坏。从这一趋势来看，则是按照Haibach法计算的结果是可以接受的中间值。

由此可以明确这一假设的基本问题为，对载荷变化过程与材料值（N_G、σ_A、k）进行静态的深入研究，并且假设材料结构是理想的。理论与试验之间产生偏差的原因在于还没有完全掌握材料机制的缺陷，这一点在图24-8中清晰地表明出来了。

举例来说，如果在图中所示的构件承受动态应力载荷，则现有的最大材料机制缺陷a_max最终对于使用寿命是最关键的。相反地，如果用构件加工出n个试样，则绝大多数情形下，试样寿命有非常均匀的分布，这里可能存在异常测值^[6]，如试样12的情形。由此可以进一步证明，前面所考察的使用寿命不是在每种情形下都是绝对可以理解的。实际中，通常在极限寿命评估或者方案比较中使用这些方法。

图24-8 试样寿命的静态分布