轻量化设计：应力载荷变化过程评估

正如轻量化结构应用领域的多样性，设计中出现的应力载荷变化过程也是多种多样的，如图24-1所示。

根据用于表示变化过程的特征值（平均值、离散）是否是恒定的或者是随着时间变化的，可判断是否存在着稳定的或者不稳定的过程。描述这些过程的特征为：

●在周期性（决定性）的变化过程中，相同应力载荷随着时间而重复发生，因此对每一个时间点，应力载荷情形的唯一可重复性是可能的；

●在稳定（随机）的变化过程中，只能对应力载荷进行静态评估，这排除了应力载荷情形的一般可重复性；

●在单振动冲击过程中，有大的初始应力载荷和衰减过程；

●在不稳定变化过程中，平均应力和振幅短时间内发生改变。

最简单的评估是评估下面的周期过程（正弦函数，即理想正弦）。一般可用强度条件求解（见VDI 2226）：

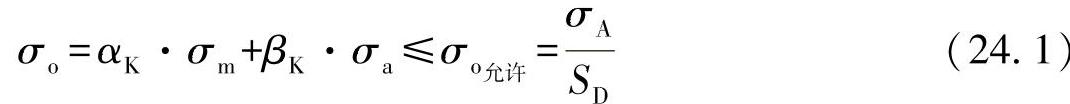
这包括两个方面，一是应力载荷在疲劳强度区域发生，二是相对于疲劳强度σ_A设置一个失效安全的上限应力σ_o。上限应力超出疲劳强度极限，则会产生耐久强度或者寿命方面的问题。从这一点来看，最终只能接受周期过程作为单级集。

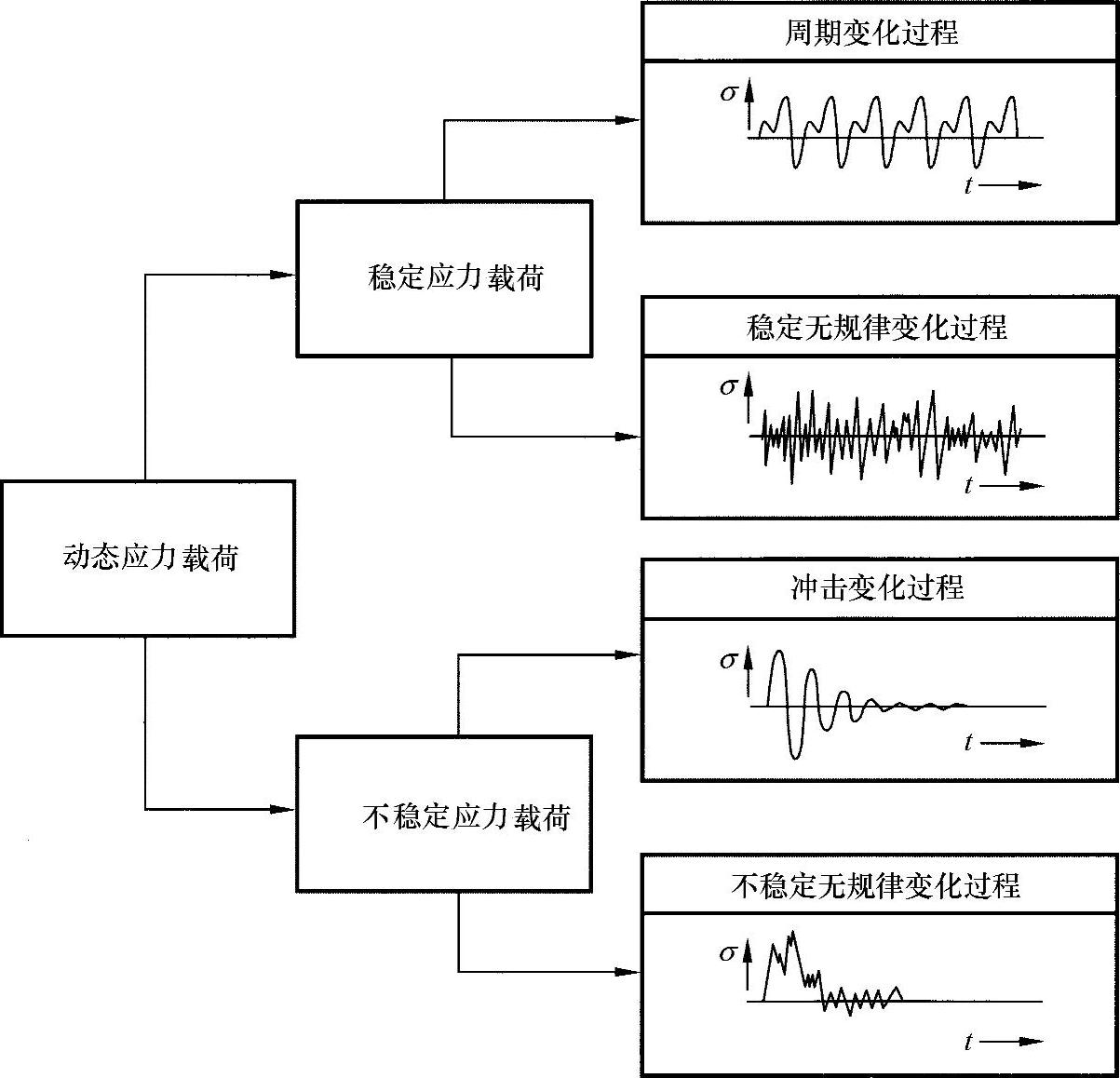
图24-1 典型应力载荷变化过程[ZAM 85]

在实际工作中，更多出现的是无规则过程，要掌握其过程顺序是非常困难的。这些无规则过程与薄弱环节的损伤行为是一致的。对于这类失效，绝大多数情况下不能取一个一次性的峰值进行评估，而需要用应力载荷结果的频率进行评估。从这一点来看，应当找到一个可用于静态判断的应力载荷函数的特征标识，以将其用于评估。为此，可使用计数技术，即有如下假设：

●可逆转换点的计数（最大值/最小值）；

●区域（下降侧面、上升侧面）的计数；

●网格内值超出的计数。

计数结果为在关于频率的顺序应力载荷图中的一个特性函数（集）。在实际应用中，一般采用等级极限超值对偶计数和区域对偶计数。图24-2所示为对一个集的考察，对应于在一个结构上的临界估计位置的等级极限超值计数。

为此，在应力载荷变化过程中设置等距网络（等级，见DIN 45667）。建议每个间距设置8～10个等级，第一等级应位于最小应力载荷之下。采用计数方法，可通过等级得到正（或者反）侧面的变化过程。振幅集σ_a（t）对于进一步的评估非常重要。根据方程式（24.2），通过两个支路的网格形计算，可求得振幅集。

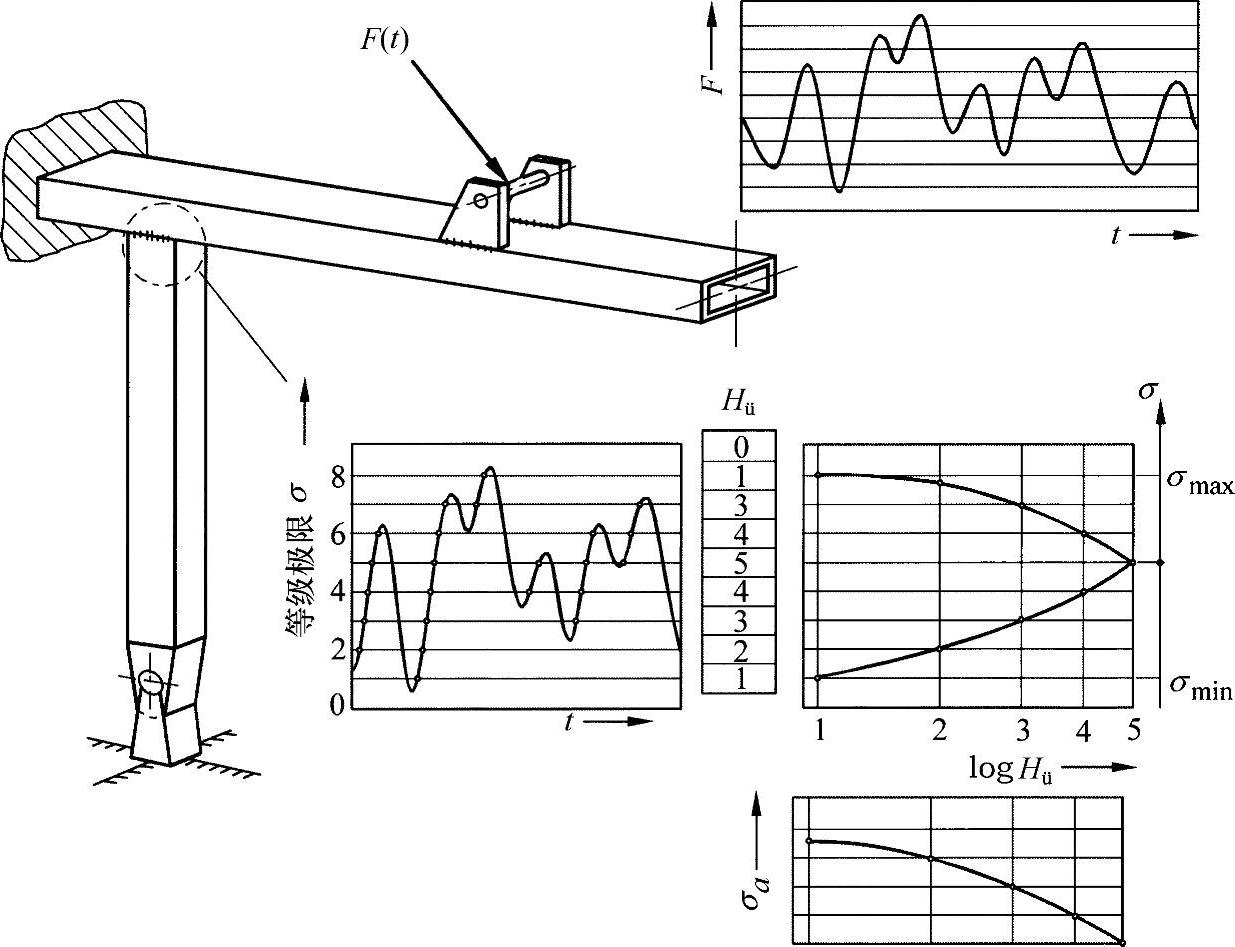
图24-2 在一个集中的应力载荷过程的转换

从中可以看出，集减少到只有一个支路。通过描述集形成的技术，从起始应力载荷变化过程中得出的振幅与频率的短时间先后顺序^[1]丢失了。

绝大多数情况下，由此得出的振幅集（测量集）只代表了应力载荷总作用时间内一个简短的应力载荷片断。从这一点来说，有必要将评估扩展到预期的总应力载荷上。为此可采用对于最大值分布的外插法，其概念由图24-3表示。其过程如下：

●首先在一个大的范围内（H_ü，N=总使用集的频率）乘以因子t_N/t_M与n_N/n_M，以对基集的超出频率（Hü，M=测量集的频率）进行换算。在对数表内，这等同于最早得出的集向右发生位移。(www.xing528.com)

●通过在任意应力载荷片断（t_i≡t_E）内进行抽样评估，可得出应力载荷最大值σ_max的分布法则，通常将其作为高斯正态分布给出。

●对于分类的极值σ_imax，可利用其排序的出现频率。

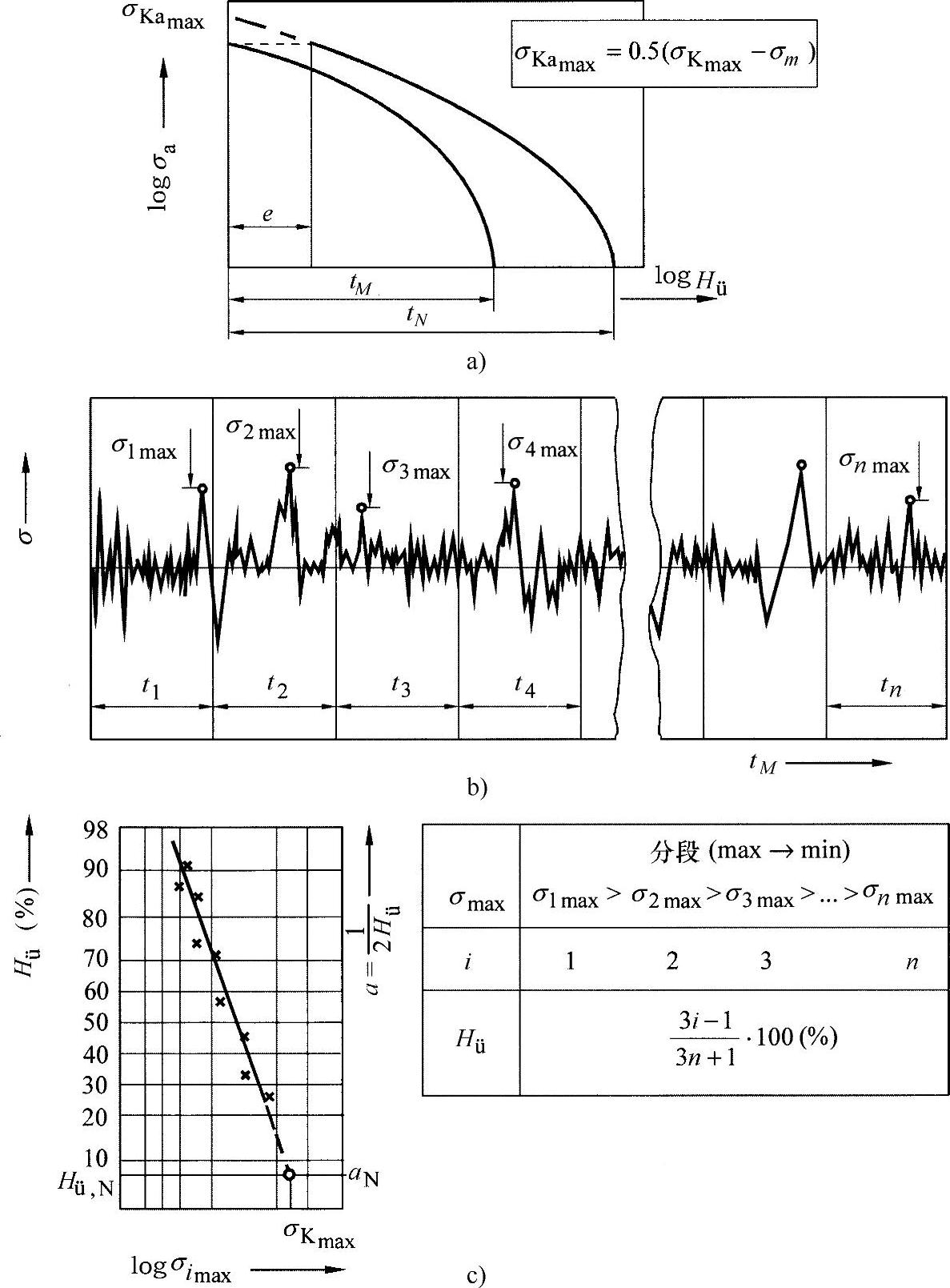
图24-3 求解集最高值的外插法

a）从测量集到使用集 b）在载荷片断内最高值的分布 c）对于a_N集最高值的计算

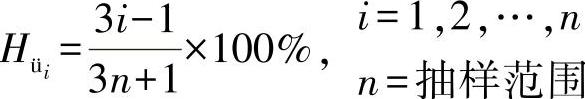
画在双对数概率纸（十进制对数）上。图通常采用直线计算。如果不能构成直线，则失效机制不服从偶然性，而是存在另外一个过程，如磨损^[2]。

●按照关系

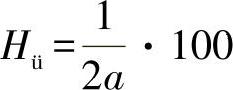
其中，

可生成超出概率与载荷片断a之间的内在关系。

●由此可得出对于超出概率的集的最高值σ_Kmax：

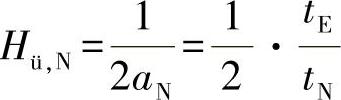
这里，对于a_N（在使用时间上的载荷片段），值可外推。

通过代入最高值，可以将初始基准集扩展到整个应力载荷作用时间范围内。

在设计方案阶段，往往不能确定应力载荷变化过程。为了能够判断一个构件的持久应力载荷性，可以使用单位集方法。经验表明，在典型应用情形下，确定的频率分布存在显著特征。图24-4对这些集的形状的分类进行了假设。

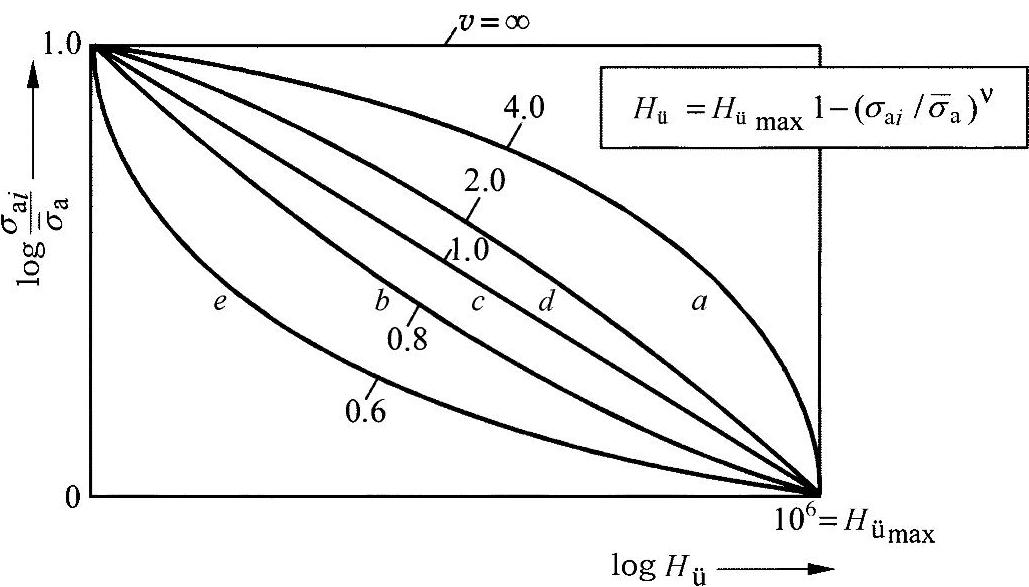
图24-4 标准化的集形状

a—λ集 b—对数标准分布 c—度线分布 d—标准分布 e—δ集

通过对比较的参数进行研究可选择出一个集，并计算出概率性的使用期限。按照约定，将范围限制在10⁶超出频率内，与相应的载荷交变相对应。这类标准集的生成与后续加工可见FKM准则。