设计方法：控制应力集中，削减应力峰值

数学上有一系列的优化战略（如Monte Carlo、梯度法、Hooke-Jeeves、逻辑框法），这些方法都可以将具有约束的函数最小化。优化任务的困难在于，必须整理出封闭有不相关参数的目标函数。在绝大多数情况下，这个函数有很强的非线性，并且还有二次最小值。这些二次最小值在优化过程中可伪装成为一个极限值，虽然它们实际上还没有达到真正的最小值。从这一点来说，与开始的设计相比较，只是有了一个改进的解法。时至今日，在设计中更多的精力通常花在了对解法策略的改进上，而不是更多关注对问题的优化，这在实际中当然是不值得推荐的。

一个注重实效的可解决实际应用问题的方法是基于计算机优化方法^[2]的CAO方法[Computer Aided Optimization（计算机辅助优化方法）]与SKO[Soft Kill Option（软杀法）]。此方法采用树木与骨骼的适应性生长作为计算机仿真策略[MAT92]。

大量的应用实例证明，基于这一方法的技术优化是可行的。由于算法简单并可在有限元方法中实现，该方法在紧凑型轻量化构件设计中得到了很好的应用，因为这一领域里总是需要进行大量的设计计算。该方法与CAO方法（构造优化）的关系在于，借助生态生长可实现常应力公理，就是说，当最大程度上掌握了应力常数，就可以认为构件设计是优化的了。

为了在一个物体中生成这样理想化的（表面）应力分布，可使用温度应变类推法，则构件优化可按照以下步骤进行：

1.前提条件是，构件有一个基本草图，在已知的工作载荷下，可对其进行有限元分析。在这种情况下，必要条件是形成一个边界平行的网络结构，因为这样可能使得构造匹配比较容易。第一个分析的结果是可得到在每个节点上的位移、应变和等效应力。

2.然后确定一个参考应力（如σ_参考=R_e），它不应超过最大的承载区域。

3.现在可以使用温度应变类推法，等效应力状态可以在如下一个假设的温度分布区域进行换算：

Δτ≡σ_V-σ参考

由此有下列类推结论：

●一个高应力载荷区对应一个热的区域；

●一个低应力载荷区对应一个冷的区域。

其设想是，由于热的区域膨胀、冷的区域收缩，最后材料必须“产生位移”。

最后，构造匹配唯一地在边界区域内实现，由此可将边界单元的弹性模量减少到大约E/500。

4.下一步可移开机械载荷，并将热微分载荷的应变：

ε=α·Δτ

作为外载荷。(www.xing528.com)

由此引进可控制的构造改变作为生长过程（位移u、v、w），该生长过程在边界区域中可假设热膨胀系数为α，在核心区域中假设α=0。这样，软的边界区域与应变变化过程得以很好地吻合。

图23-7 CAO方法原理流程

图23-7表明了如何将这种方法转化为计算机可执行的策略，这一过程在程序KONTOPT中得以实现[FREI 94]。

大量的对二维和三维构件优化的应用实例证明了这种优化方法的实效性。图23-8所示为一个假设的例子：体积角。作为测试件，该构件在短的端面加以固定，在长的端面的上棱角则承受均匀线性载荷。

可预期的是，在缺口处会有一个很高的应力集中。为了控制这个应力集中，每个设计师都会对角进行圆整。温度应变策略也采用同样的方法，通过轮廓位移对应力变化中角的表面进行补偿。

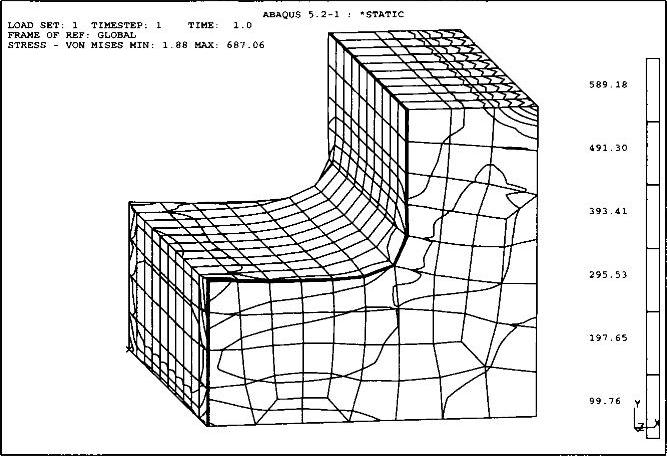
图23-8 优化示例：“角”，材料为46Cr2——优化后的轮廓变化

在轻量化设计中，也可以考虑采取其他的措施来削减应力峰值，如设置加强肋。图23-9所示即为一个采用这种方法的紧凑型构件。

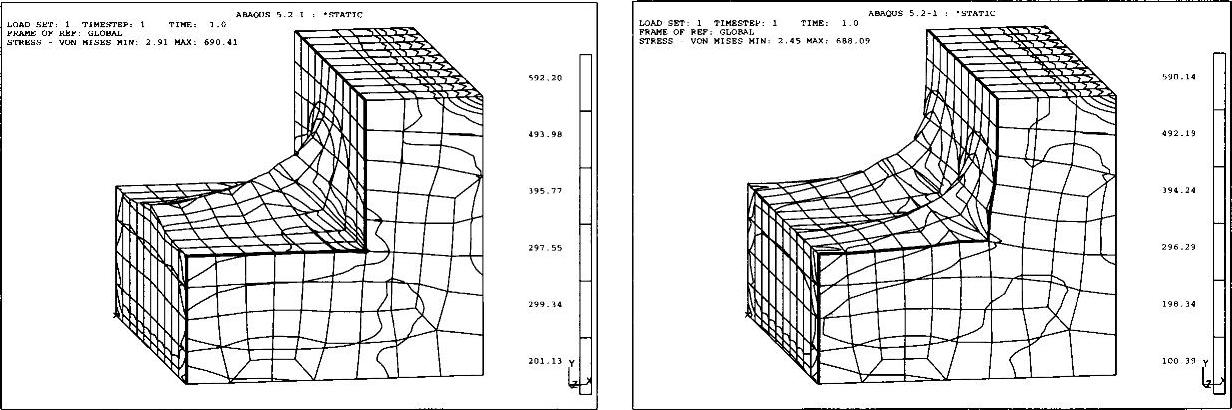
图23-9 生成应力控制的加强筋，作为圆整的替代方案

a）通过一根加强筋抵消应力 b）通过两根相同的加强筋抵消应力

设计师可以确定加强筋生长的位置，通过主应力轨迹线的方向和大小可得出几何尺寸。这样，就有了一个容易使用并且可靠的方法，该方法也已经得到了广泛的应用。

加强筋算法也可以用于板材构件的卷边计算中。要实现这样的计算不仅可以采用KONTOPT软件，而且也可以采用很多其他的商业软件，如TOSCA。