轻量化设计：抗弯杆重量最小化

在钢结构设计中，经常用抗弯杆作为附加的加固件，为此通常应对其进行重量最小化设计。可设定的已知前提条件是，横截面的形状对承载能力有影响。为了说明方便，这里采用圆形和正方形的实心横截面进行研究。图23-5所示为假设的比例关系。

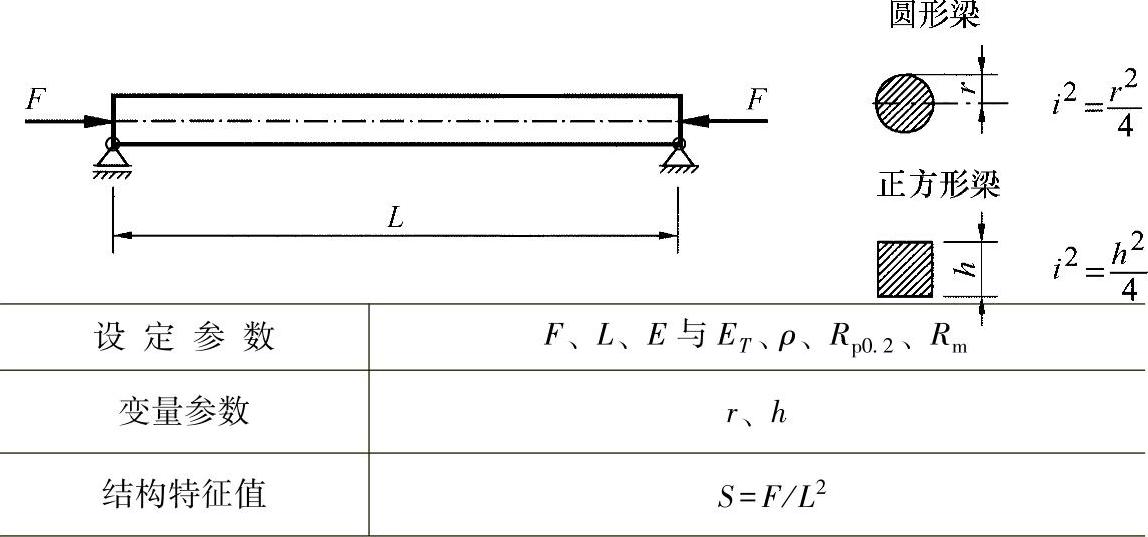
图23-5 圆形与正方形实心横截面的压杆[WIE 79]

作为设计约束，允许的抗弯应力[见方程式（18.28）]：

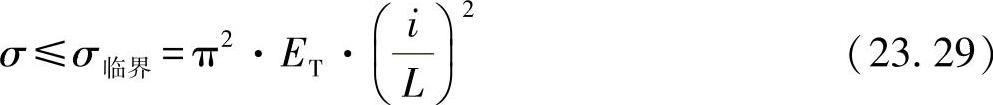
其中，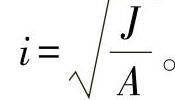

应在非线性区域计算。对于重量，有：

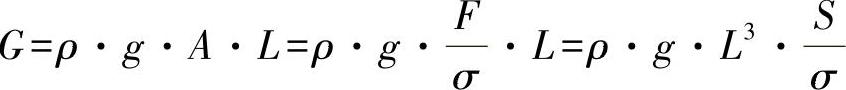
与

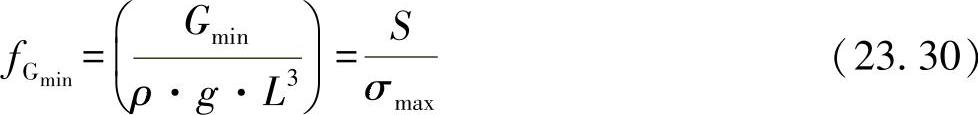
从该方程可以看出，应力的最大值等效于重量的最小值。

对于这两种横截面形状，其应力可计算如下：

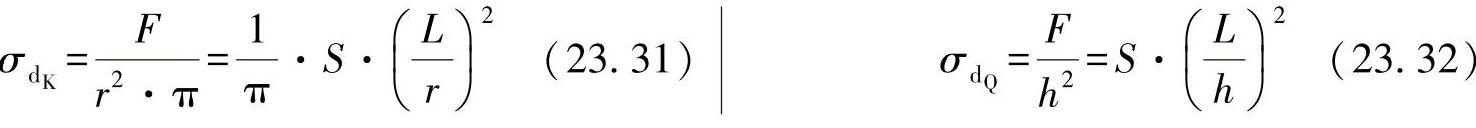
考虑到约束，得出优化的变量为

或者

每一个变量可作为无尺寸比例关系，借助结构特征值给出：

(https://www.xing528.com)

将优化的变量代入相应的应力关系式（23.31）/（23.32），可得出：

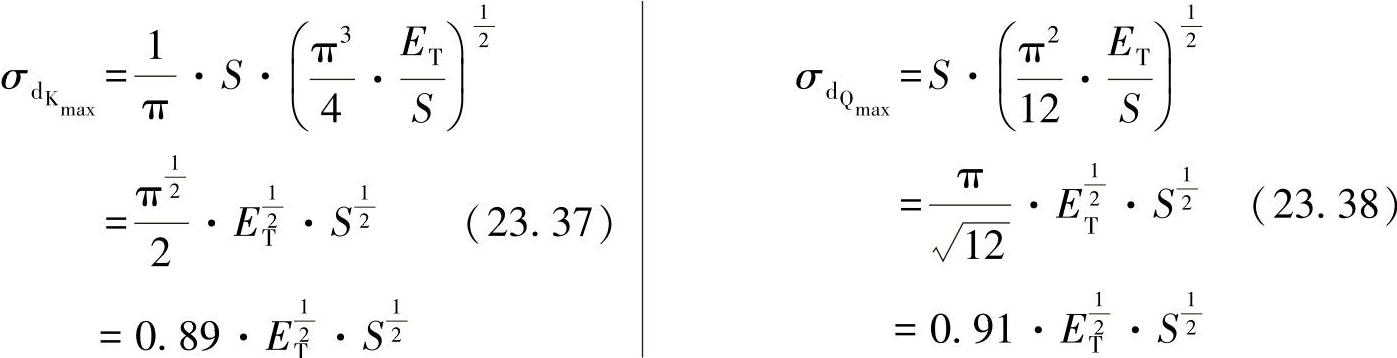
与圆形梁相比，正方形梁抵抗压应力的能力改善很少，因为材料都设置在外区域了，即有：

作为以上研究的补充，应进一步说明同类型的空心横截面设计的情形。其可能的比例关系可假设如下，给定的比例是（r/t）与（h/t），需要优化的比例为（r/L）与（h/L）。基于此，可计算两种横截面形状的应力为

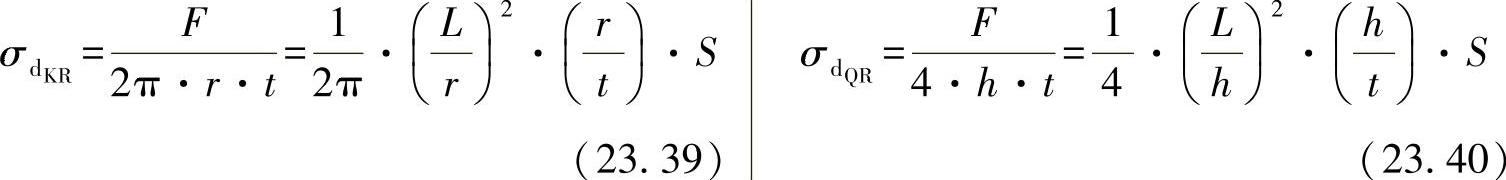
对于有临界应力的极限条件^[1]：

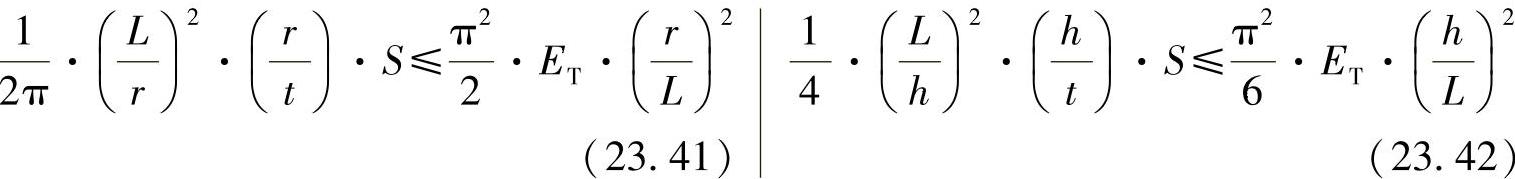
可重新得出优化的比例为

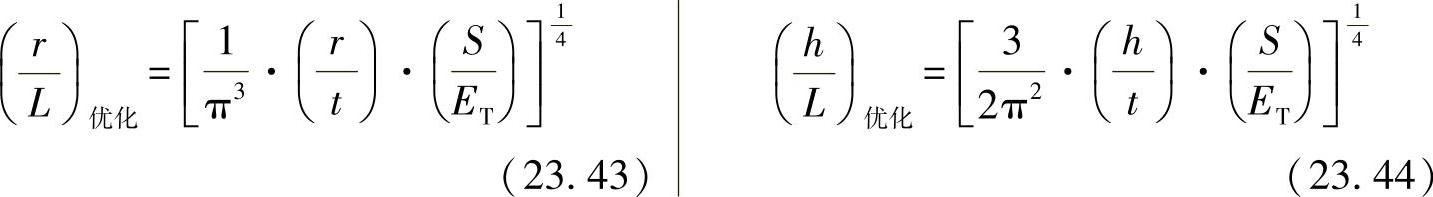
将其重新代入所属的应力关系式（23.29）/（23.40），可得出：

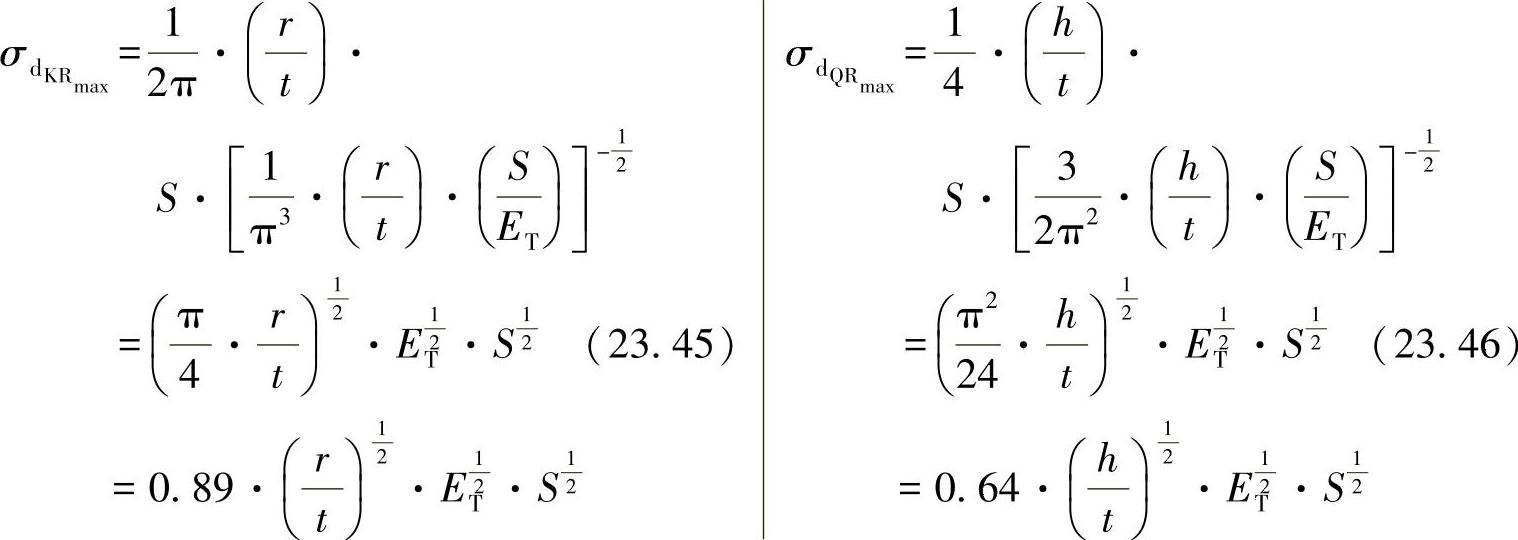
当h=2r时，相比较有：

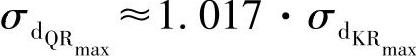
根据情况可以利用圆形和正方形的优点。图23-6中表明了对于这些型梁的σ对S的变化过程，当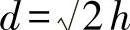时，有。

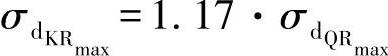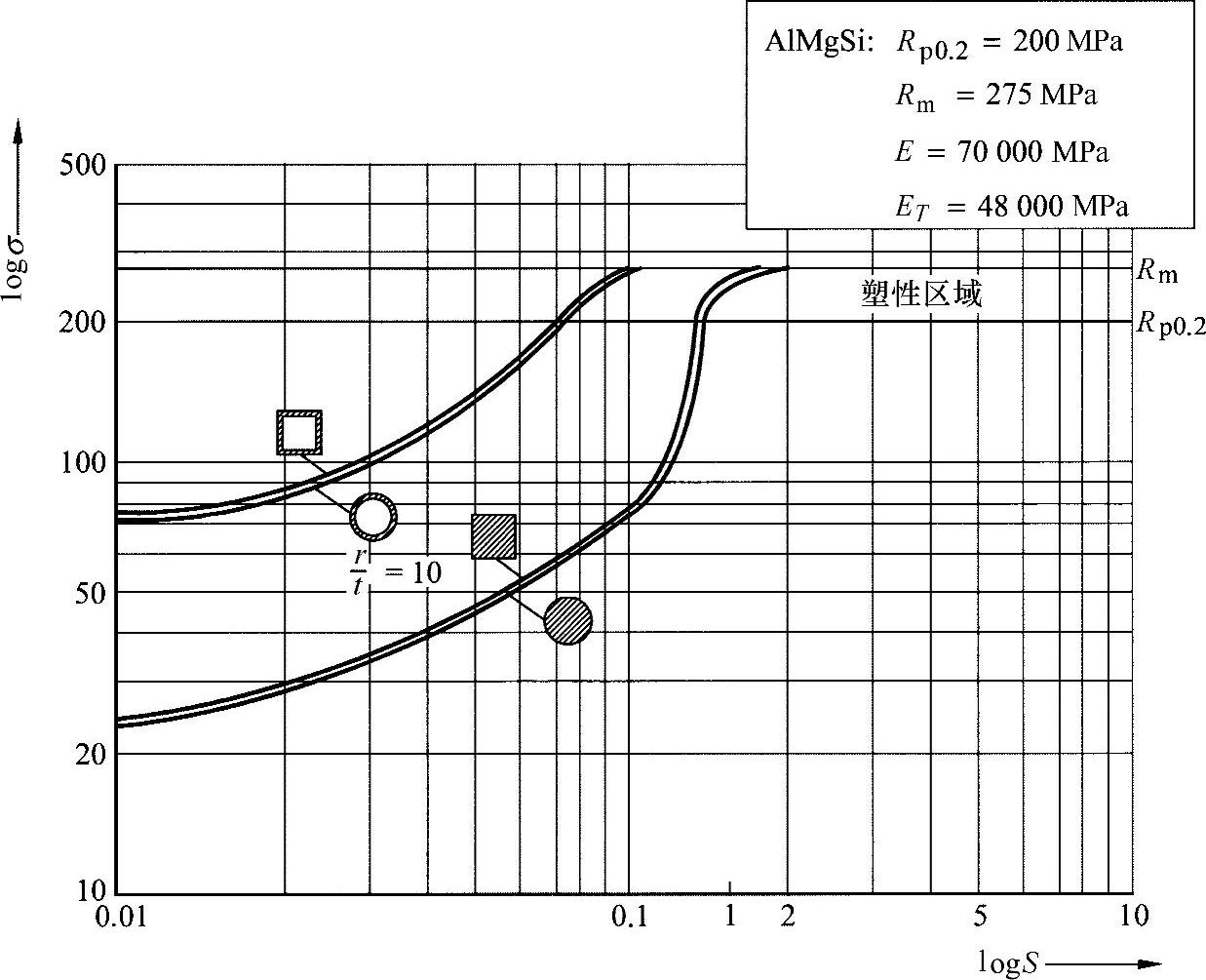
图23-6 实心横截面抗弯杆与管横截面抗弯杆的使用范围