【摘要】:设计中经常碰到的一个问题是,在刚度和强度约束下实现抗弯梁的重量最小化。由此,对于一个最小化设计有极限为●刚度问题●承载能力问题图23-4所示为与变量比例h/L有关的目标函数变化过程。图23-4 具有可替代设计极限的目标函数
设计中经常碰到的一个问题是,在刚度和强度约束下实现抗弯梁的重量最小化。图23-3表示了一个这样的情形,这里简化为一个正方形的型梁。
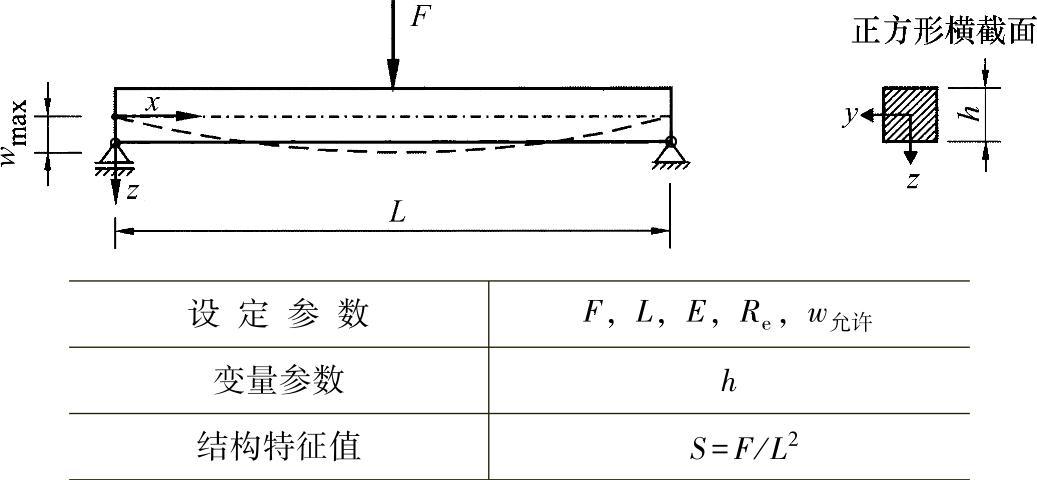
图23-3 正方形全横截面的抗弯梁[WIE 96]
在刚度优化中,必须将允许的挠曲作为变形条件加以考虑。

型梁变量的大小由所要求的面积惯性矩来确定:

刚度约束可适当地计算为
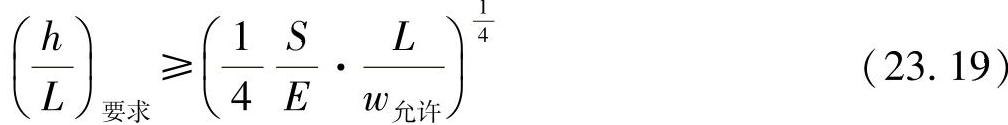
对于梁的重量,可有:

这样便可按照方程式(23.15)整理出主要的重量函数为
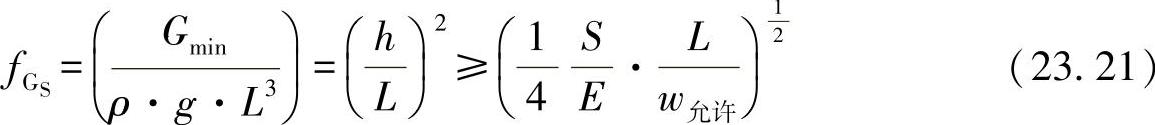
对于强度优化,须有弯曲边界条件:
σxx边界≤Re (23.22)
按照上式,根据所要求的阻力矩可确定型梁变量的大小为(https://www.xing528.com)

对于强度约束有:
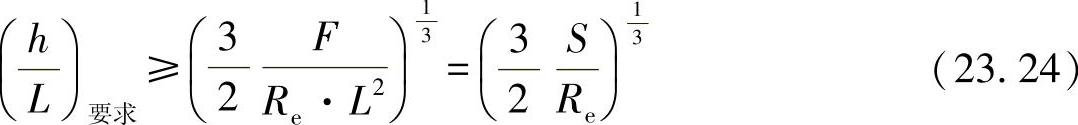
这里,与刚度有关的重量函数又可改写为
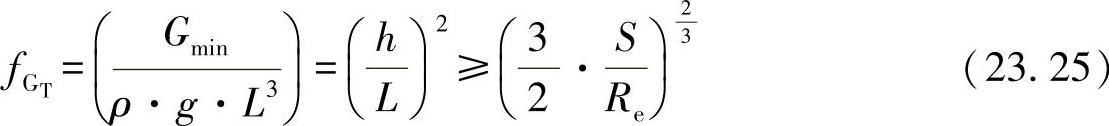
为了将这些约束[方程式(23.19)、(23.24)]用作目标函数的极限fG,S/T,可借助结构特征值和基准值:

将其标准化。由此,对于一个最小化设计有极限为
●刚度问题
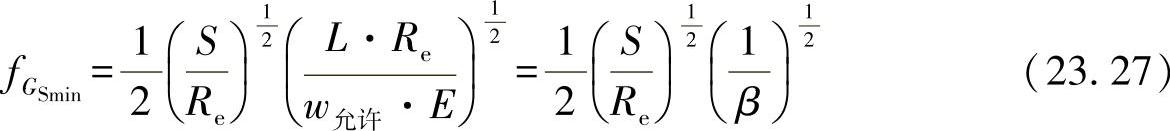
●承载能力问题

图23-4所示为与变量比例h/L有关的目标函数变化过程。由于经常需要用很小的参数来确定基准,所以这里选择了一个对数图。这两个约束条件限制了不允许的区域。基于刚度和强度的原因,不可超出这个区域。
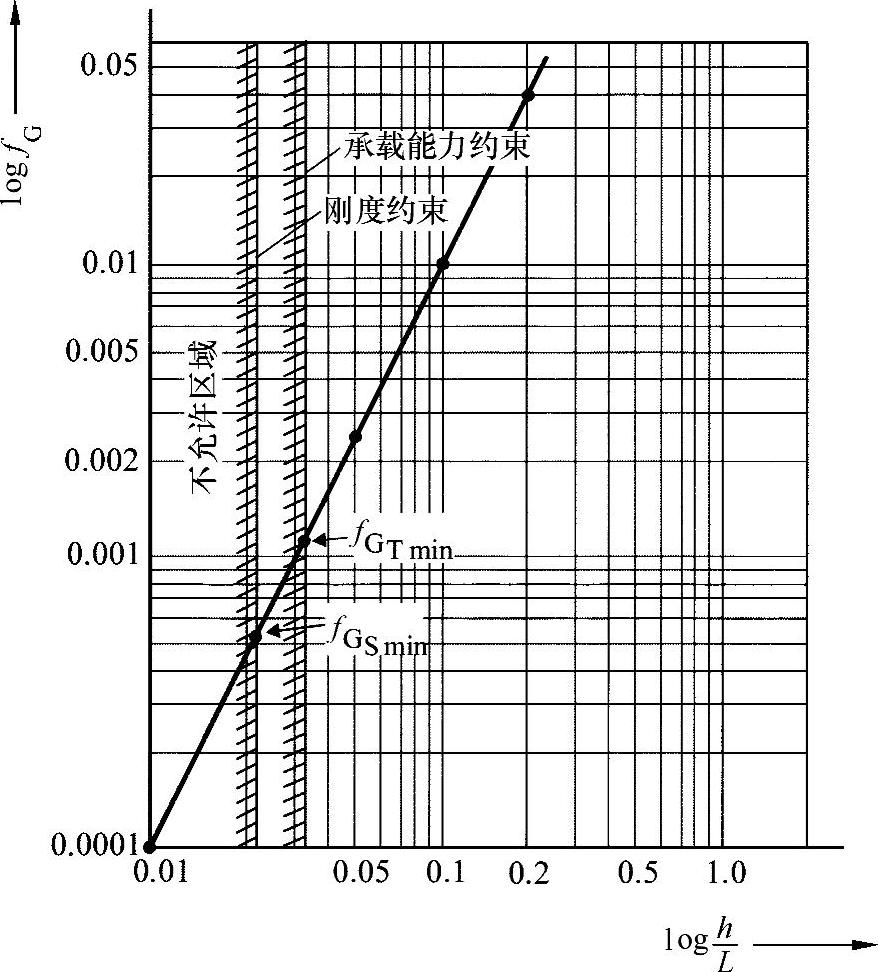
图23-4 具有可替代设计极限的目标函数
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




