轻量化设计中法向应力的估计方法

如上面提到过的，在广义的连接技术中，除了会出现切向应力外，还会出现法向应力。下面将在单截面粘接连接上，计算法向应力的大小。这里研究两个法向应力，σ_xx与σ_zz。

在图22-14中可看出，由于粘接产生的法向应力σ_xx，上面的盘被分离出来，并通过内力变量达到平衡。

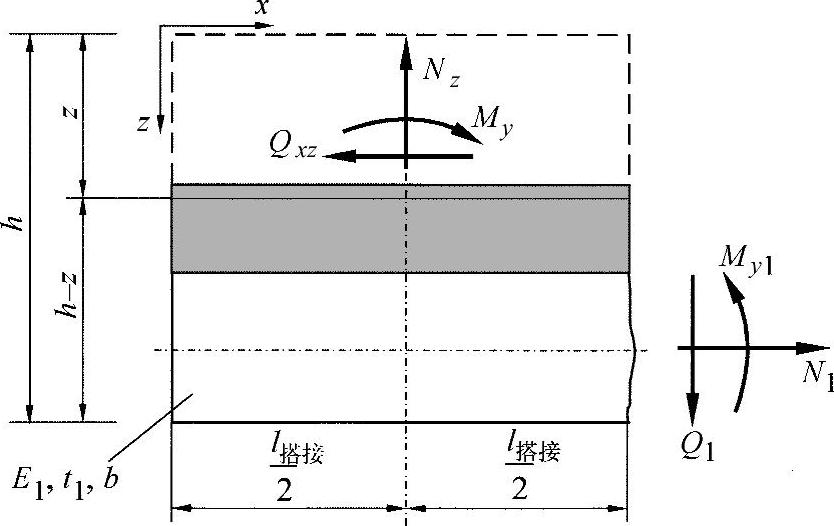
图22-14 z方向上粘接缝的平衡

内力为

N_z=Q₁

Q_xz=N₁

与

M_y（z）=M_y1+N₁（h-z-0.5·t₁）-Q₁·0.5·l_搭接

据此，可求得最大法向应力为

经过转换，可进一步得出关系：

由图22-15可以看出，法向应力σ_xx也会出现，可以在图中所示的截面单元上对其进行求解。

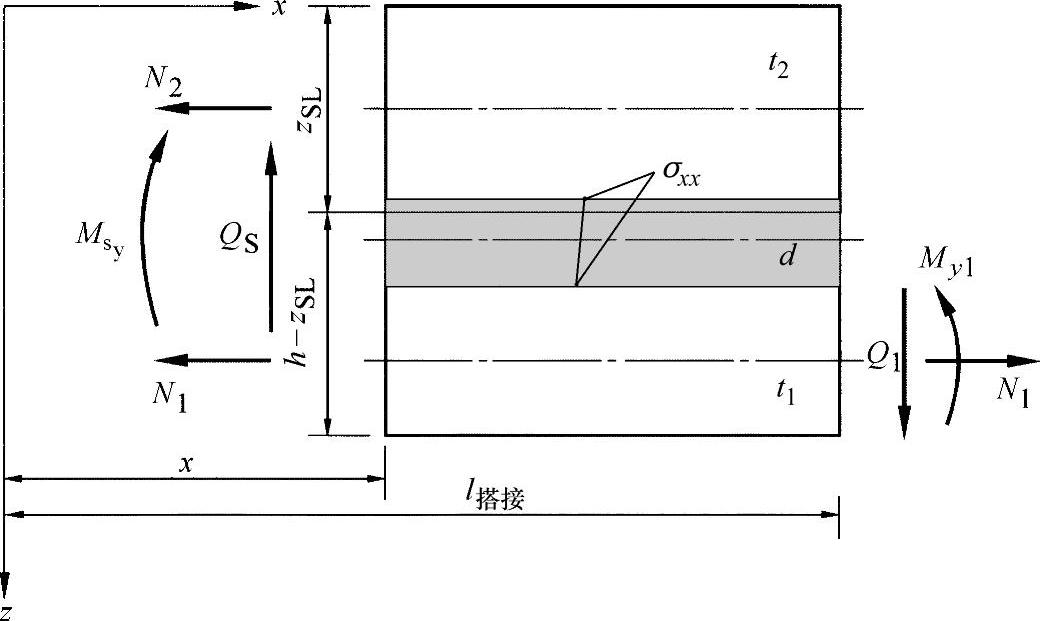
图22-15 x方向截面上粘接缝的平衡(www.xing528.com)

重心线的位置对应力载荷的大小来说很关键。考虑到盘可以由各种材料构成，则相应的坐标为

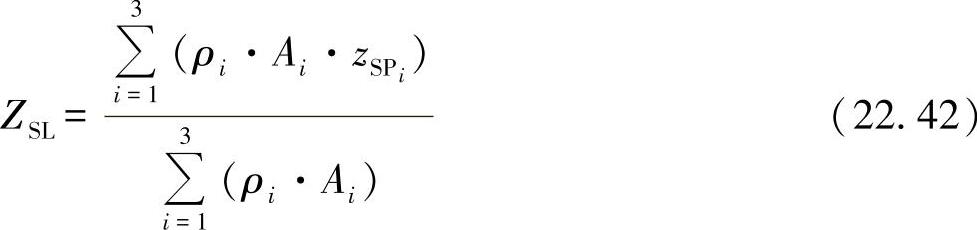
由此可计算出弯曲力矩为

M_Sy（x，z）=M_y1+N₁（h-z_SL-0.5·t₁）-Q₁（l_搭接-x）

而应力可以确定为

根据具体情况，外缘纤维距离为

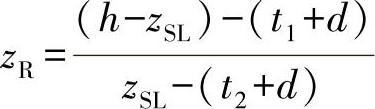
相应地，最后所产生的面积惯性矩为

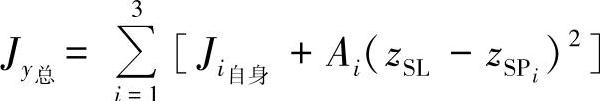
一般来说，由于σ_xx<<σ_zz，因此在绝大多数情况下可以将其忽略。粘接层中所产生的应力可以按照切应力假设计算为

因此，可计算出应力升高比：

通过以上计算证明了，粘接时必须要考虑到弯曲对连接应力的影响。在弯曲作用下，连接应力可增加25%。有限元计算方法结果则表明，在弯曲作用下，连接应力增加幅度为30%～35%。