切应力载荷下粘接连接中的应力分布

以往都是将粘接的载荷性能（连接强度）控制在简单的强度条件下：

即以前的要求是粘接材料中的平均切应力应当小于拉伸-剪切断裂强度。

新的强度理论分析证明，这一表达式太过简单了，甚至是错误的，因为在搭接长度上的切应力变化过程中部分地显示出了大的峰值。

为了进一步研究起见，假设有图22-9所示的单截面粘接连接。只有在简化

图22-9 任意材料组合的单截面粘接连接

的情形下定义了下列前提条件，才可能得出充分准确的分析：

●所有沿着接缝的横截面保持恒定；

●所有连接件包括粘结剂的行为都是线弹性的；

●在接缝处不出现弯曲力矩。

1938年沃克森已经就这一问题进行了说明[VOL 38]，由他的推导衍生出多种变体（如[MÜL 61]、[MAT 63]）。下面将介绍一个非常重要的改进解法。

求导的插入点为在粘接材料边缘层的位移与在两个连接件中的应变之间的关系，如下所示。对于在任意位置上连接内部的位移有：

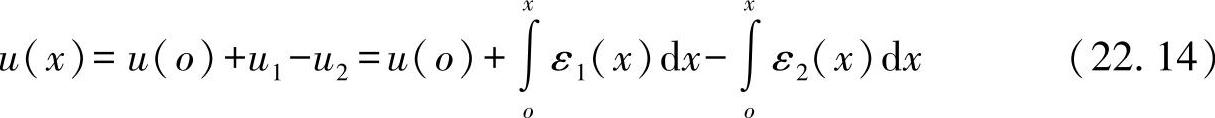
连接件内的应变为

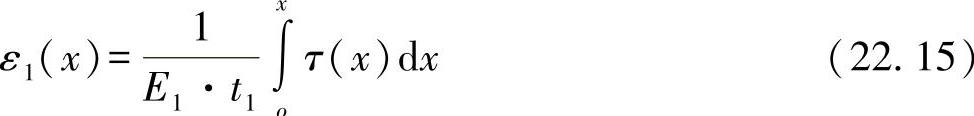
与

将该式代入方程式（22.14），可得出：

现将该方程两次求微分，可有：

假设在粘接材料内只有剪切力（图22-10）在作用，则有：

图22-10 自由截面的粘接连接

在微分方程（22.18）中考虑到这一点，则有：

其中，

对于这一均质微分方程第二阶，其解法已知为

u（x）=A·cosh（λ·x）+B·sinh（λ·x） （22.22）

这里存在两个位移边界条件：

u（x=o）=u（o） （22.23）

与

u（x=l_搭接）=u（l_搭接） （22.24）

左、右边界两个位移都相同的假设，只发生在材料相同的情况下。对于一般的情况可给出如下的关系：(www.xing528.com)

u（l_搭接）=u（o）+Δ （22.25）

采用这种数学方法可清晰地求解该问题。对于方程式（22.20）来说，现在没有完全求证的位移为

这里还引入了另外一个常数β，其定义为

下一步要寻找的不是位移，而是应力。可在如下线性比例中得出：

与

上述的方程是由平均位移与平均应力形成的。

由此可求得平均位移为

对于方程式（22.28），则有：

与此相反，如果现在用：

引入另外一个参数值，则方程式（22.31）也可以写成：

由此，可得出室温下粘接连接沿轴向的应力分布为

该方程有一个极限值，根据材料组合或者在左边界或者在右边界而定，并且或者在：

或者

对于应力载荷的讨论，切应力峰值也可以借助一个升高比（kτ），定义为

τ_max=kτ·τ_m （22.37）

这里，根据上面在左接缝终端或者右接缝终端的边界条件使用升高比进行计算。对于各种切应力变化情形，在图22-11中根据方程式（22.34）将其可视化了。为了解实际的不同，下面选择了三种不同刚度比例关系。

从图中可以看出：

●在相同的材料配合情况下，会出现对称的切应力分布，最大值在边界出现；

●在不同的材料配合情况下，则出现不对称的切应力分布，最大值总是出现在搭接的边缘，并且是在刚度较高的连接位置，即在比较厚的板材上。

如果粘接连接的终端变得尖锐，则理论上可以得到一个均匀的、峰值明显很低的应力变化过程。这种盘的弹性与粘接材料的弹性会配合得更好，从而消除了应力的峰值。这一结果与前面结果的比较如图22-12所示。

图22-11 抗弯钢板不同材料组合下应力升高比kτ的变化过程

图22-12 切应力下尖锐的单截面粘接连接

当一个对称的、不尖锐的连接的应力升高比k_τ=3.098时，一个与锐角α相关的尖锐连接的应力升高比则减小为k_τ=2.134与k_τ=1.414。反向推论则有：在纯线性比例关系下，一个尖锐连接承载能力明显得以提高（1.45～2.19倍）。从这一点来看，尖锐化是一个可以更好地利用连接方式的方法。