常应力导入弦杆：轻量化设计技巧

弦杆的任务是通过板材将外力加以卸载。从这一点来说，弦杆应有足够的弹性，以使得板材可以逐渐地承受力。为此，要求弦杆的横截面具有可变的刚度变化过程。

图21-4为一个三弦杆盘，其中，传导弦杆的横截面是变化的，而边界弦杆的横截面则不变。对传导弦杆来说，应满足以下要求：常应力以及等效的常应变（ε′₁=u′₁=常数）。

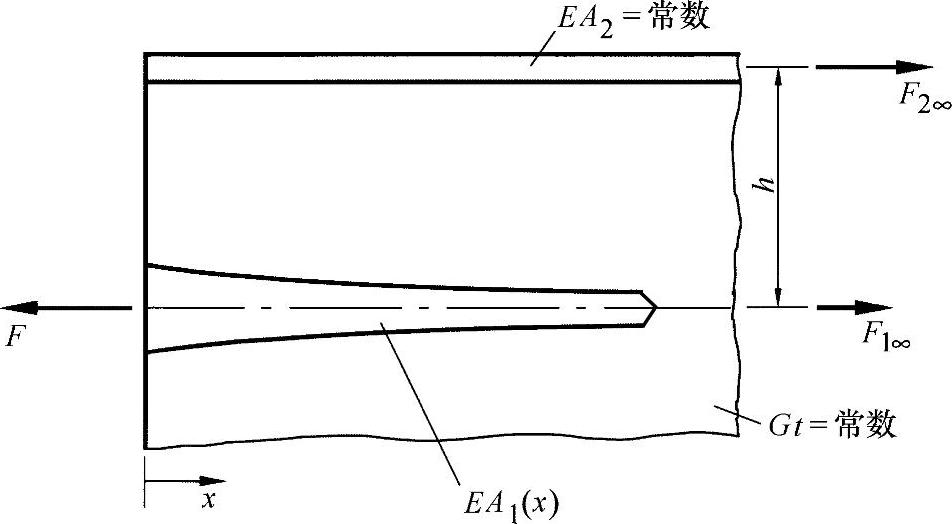
图21-4 三弦杆盘，导入弦杆的应力为常数

上述问题的初始条件为平衡方程式（21.1）～式（21.4）。这些方程式可如下计算：

●对于可变的导入弦杆：

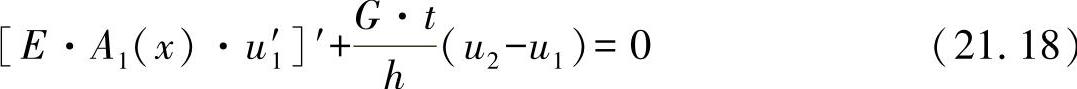
●对于边界弦杆：

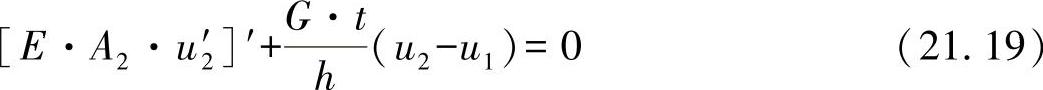
如果将这两个积分加以微分，则对方程式（21.18）有：

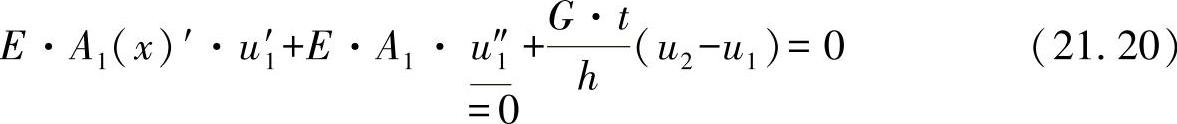
由于已假设导入弦杆u′₁=常数，所以u″₁=0，并且有：

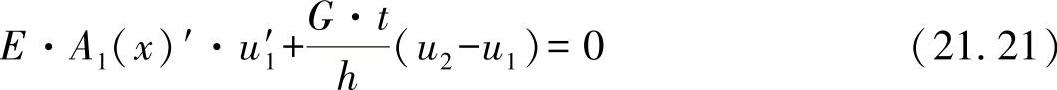
对于边界弦杆已假设有E·A₂=常数，因此方程式（21.19）也可以写成：

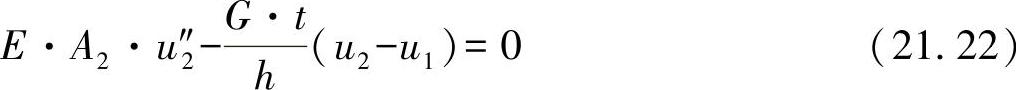
这种情形的边界条件是特殊的变形条件（很容易推导出前面的条件）：

●x=∞：γ=0

●x=0：u₂′=0，u′₁=常数。(www.xing528.com)

这些条件无须明确地证明，通过下面的表达式即可满足（见[WIE 79]）：

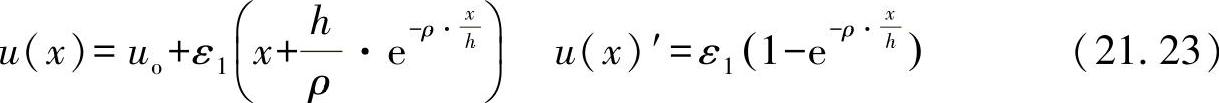
与

㊀ 终端横截面A₁∞须根据设计条件加以确定，而初始横截面A₁（0）可自由选择。

这样一来，可将在弦杆上的力变化过程加以量化：

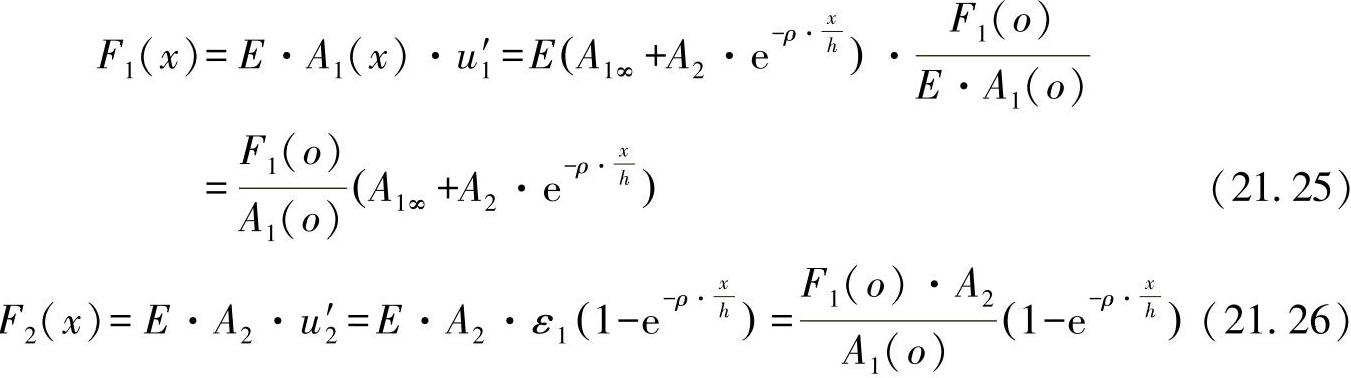
在板材上卸载的边界剪切力变化可进一步由弦杆上的平衡方程[见方程式（21.2）]求出，即有：

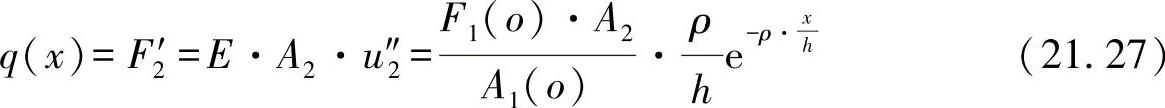
三个力变化的原理如图21-5所示。

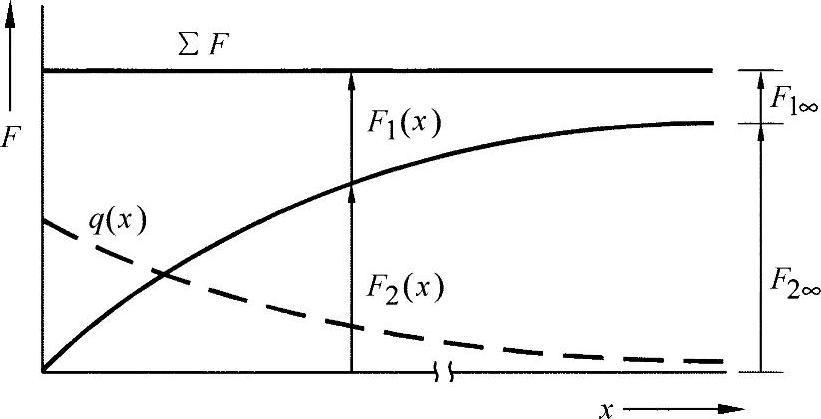
图21-5 加固盘上力的变化过程，盘上有匹配的导入弦杆

从图中可以看出，在边界弦杆上，力迅速发生了转移，从而使板材得以卸载。

与此相关的一个问题是：导入弦杆的长度多长是合适的。由条件F₁（x）=0，方程式（21.25）可变换如下：

如果选择了沿着长度上的一个三角型材作为导入弦杆，就不需要进行以上的繁琐计算了。