轻量化设计：三弦杆盘的力学模型与结构探讨

下面举一个典型的例子，即分析一个简单的三弦杆盘，对应于机车车厢的地板结构，中间力的导入要通过离合器。图21-2所示为力学模型，同时也是上面分割部分的开口。设想是将集中在弦杆上的力，通过剪切力传递到板材上。从这一点出发，需要考虑在设计的结构长度上不同刚度之间的相互影响。

根据弦杆上的平衡条件，可得出必要的关系：

●对下弦杆，有：

图21-2 局部两弦杆断面上的力平衡与变形行为

F′₁+q=0

●对上弦杆，有：

F₂′_-q=0 （21.2）

在弦杆上，进一步可得出如下的弹性关系：

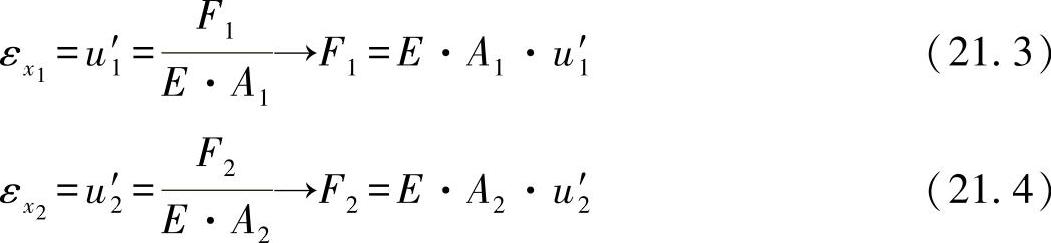
对于剪场来说，则有扭曲条件：

由此，可得出扭曲盘边缘的剪切力流为

因此，力的传递可通过微分方程式（21.6）与方程式（21.7）加以描述：

即，弦杆比例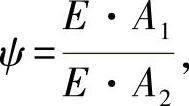

则有

切应力则为

对均质微分方程式（21.8）

q″-α²·q=0 （21.9）

可由方程式：

得出求解表达式。由特征方程，可求得指数为

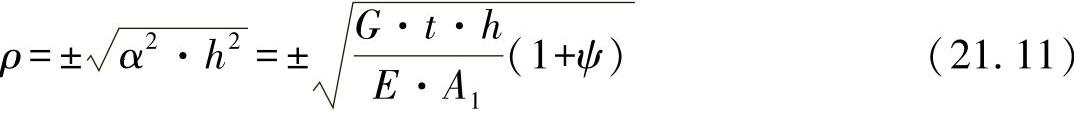
根据满足微分方程的基本定律，可得板材上剪切力流变化的解为

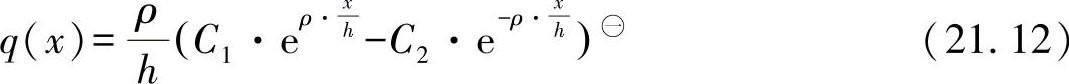(www.xing528.com)

㊀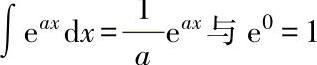

由方程式（21.1）与方程式（21.2），通过积分可进一步求解，例如：

或者

只有在给出边界条件的情况下，上面的解[WIE 79]才可以明确地加以确定，例如：

●在长盘条上实现完整的力转移：

x=∞：q=0→C₁=0

F₂=F₁C₂=-C₀

●直接在力导入位置：

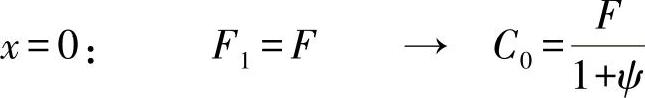
根据以上方程可得出力的变化为

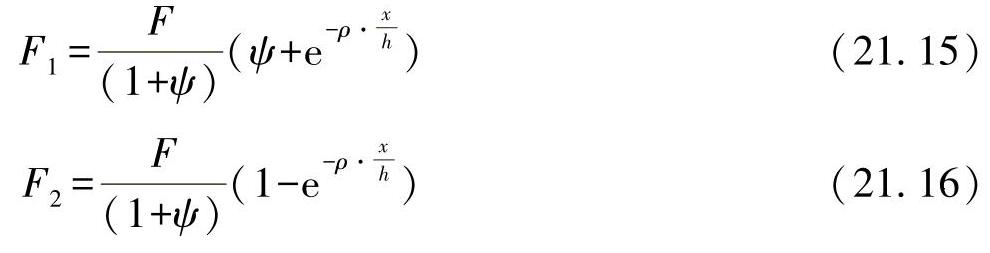
与

●一端固定的与具有相应的对称条件的对称盘条（如一个汽车地板组很长的域）

x=0：q=0

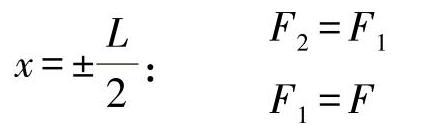
通过讨论方程，可得出相应的力变化为

与

其中，基准刚度值为

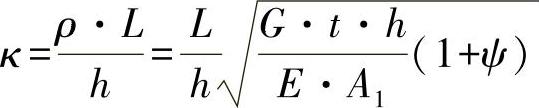
图21-3描述了上面两个例子中力的传递原理。

图21-3 轴向弦杆-盘模型上力的变化[WIE 79]

a）非常长的盘条 b）一端固定的对称盘条