型材的凸起及其设计原理

如同平面桁梁一样，型杆的壁也有凸起的倾向，特别是局部凸起，这可通过短波纹凸起形状来加以标识。在型杆压弯时，横截面形状保持不变，杆轴发生偏移；而在型杆凸起时，型壁的连接棱是直的，只是壁产生凸起。图19-10所示为凸起示意图。

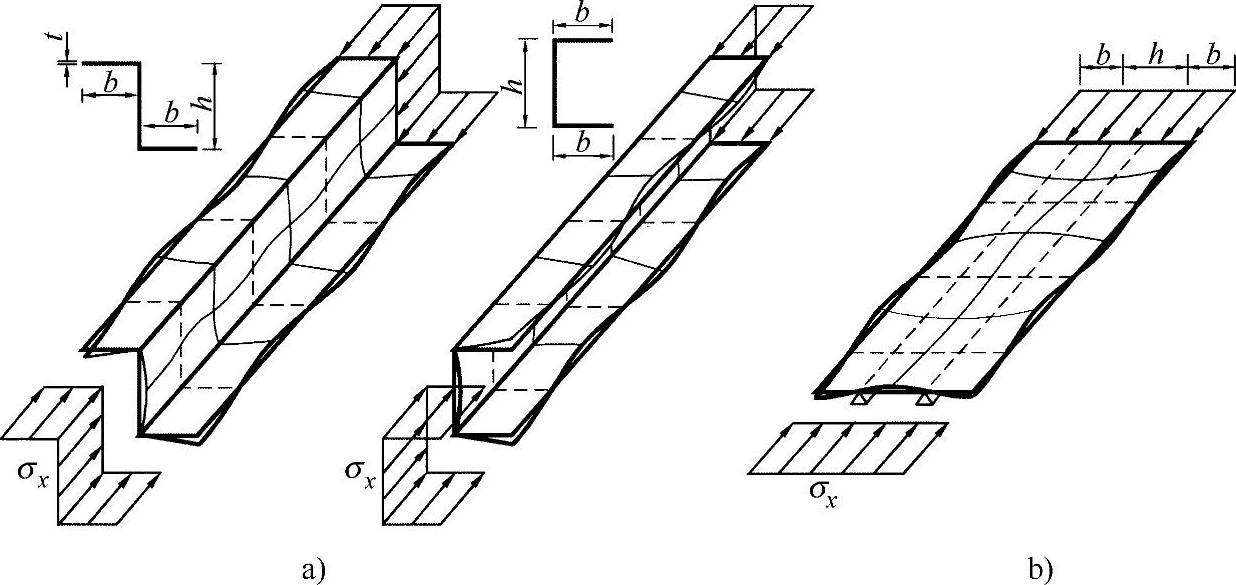
图19-10 型杆的凸起图[WIE 79]

a）在型材上 b）在展开区域

这一效果可归因如下，即所有产生的弯曲都像支座那样稳定，所以可作为凸起波纹的节线起作用。因此，应力载荷总是强迫型杆变形成一定的凸起形状，以至于从本质上讲，型材在哪个方向上发生弯曲都不重要了。下图示例中显示了两种情形，最后也都可以归纳为带有铰支的板条。

如图19-11所示，对于这些基本形状，有以下基本方程：

情形a）板条，两端铰支

凸起的波长为m=h，凸起临界应力为

情形b） 板条，两端固定

凸起的波长为m<h，凸起临界应力为

情形c） 板条，一端铰支，一端自由

凸起的波长为m=L，凸起临界应力为

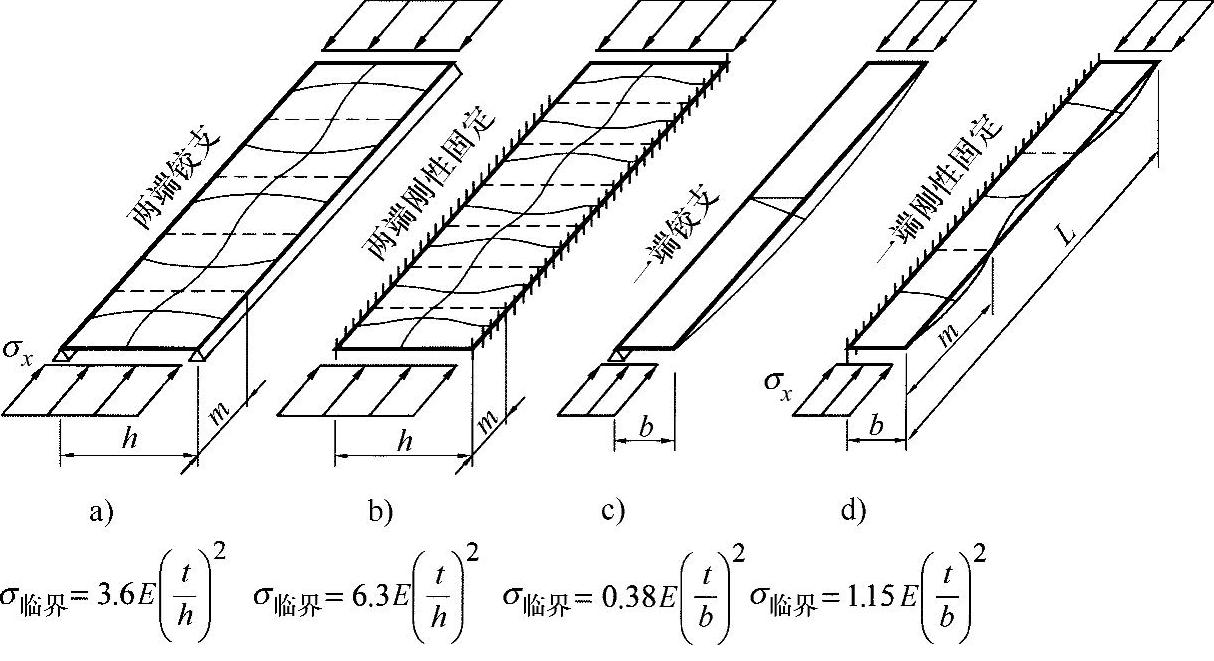
图19-11 型板带的凸起形状与凸起值[WIE 79]

情形d） 板条，一端固定，一边自由

凸起的波长约为b<m<h，凸起临界应力为

上面列出的方程可直接由图19-7导出。(www.xing528.com)

现在可以用这些单个的板条来组合构造型材。由于单个的板条在边缘是组合在一起的，这里的边缘角与半波长必须是一致的。这种束缚作用的结果是，在每种情形下，型材的凸起应力都大于不稳定的单个板条的凸起应力总和。在固定拉紧时，总是会在支承作用上限的范围以内。

如果现在来计算型杆的凸起应力，采用型材中的力平衡方法[ÖRY 83]会更简单一些。

对于图19-12中所示的角型材有方程式：

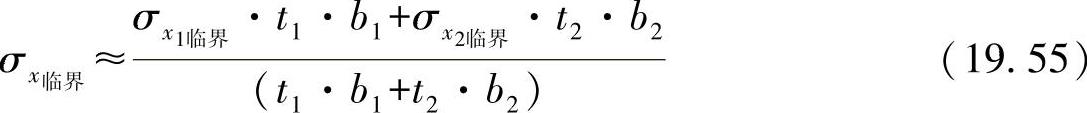
根据型材的几何形状，可将角型材分为两个板条，二者通过一个刚性的棱连接在一起。通过计算可以得出：

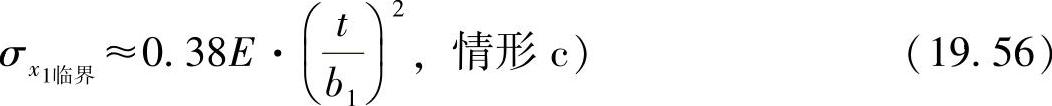
与

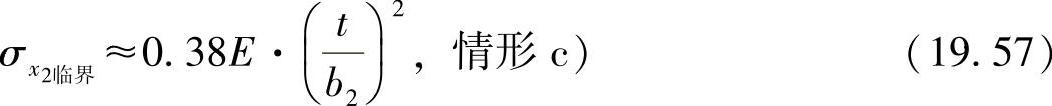
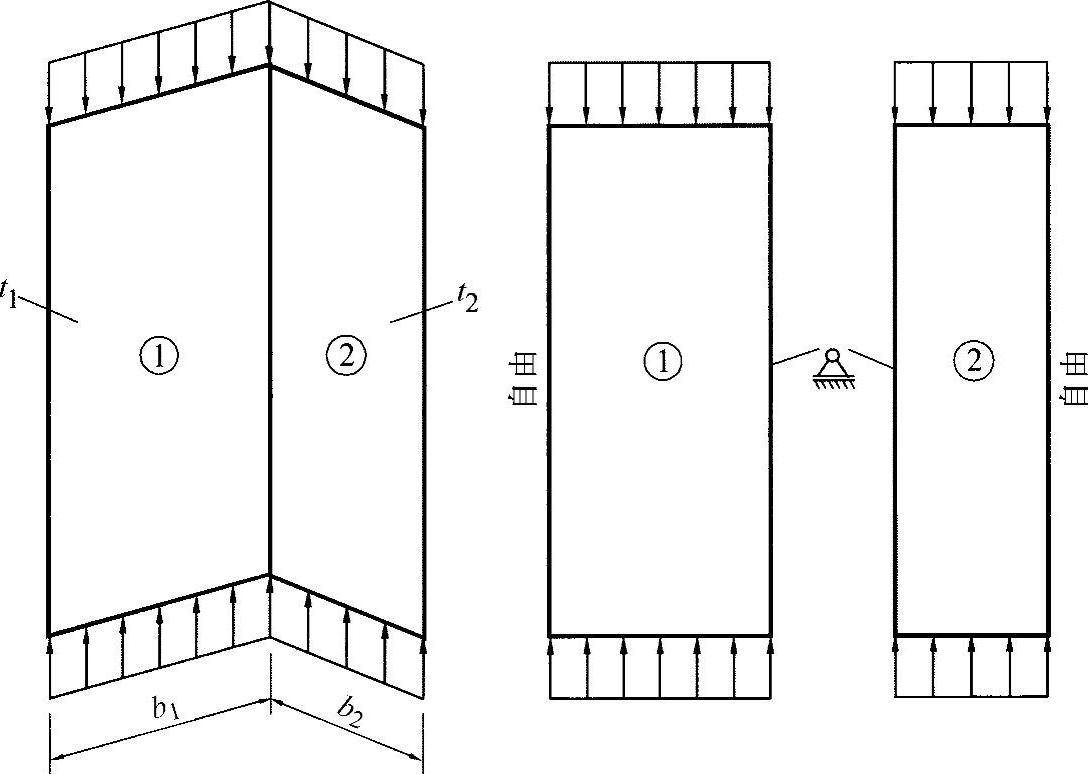
图19-12 简单角型材

上述表达式可概括为

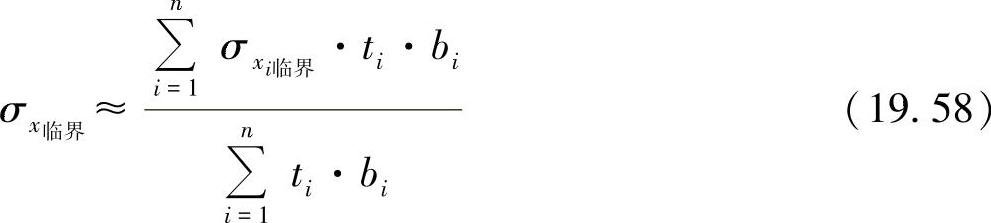
对于方程式（19.58）的总结性评估见图19-13中的Z形型材。如其几何构造所示，型材可分解为三个板条，这样就有两次带有自由边界的板条，通过计算有：

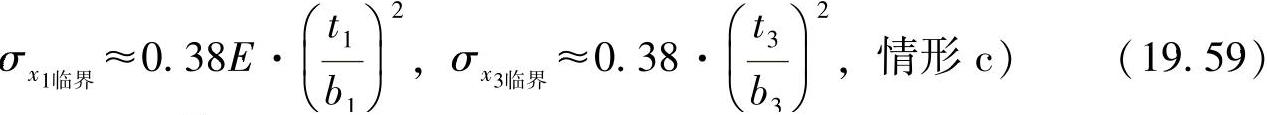
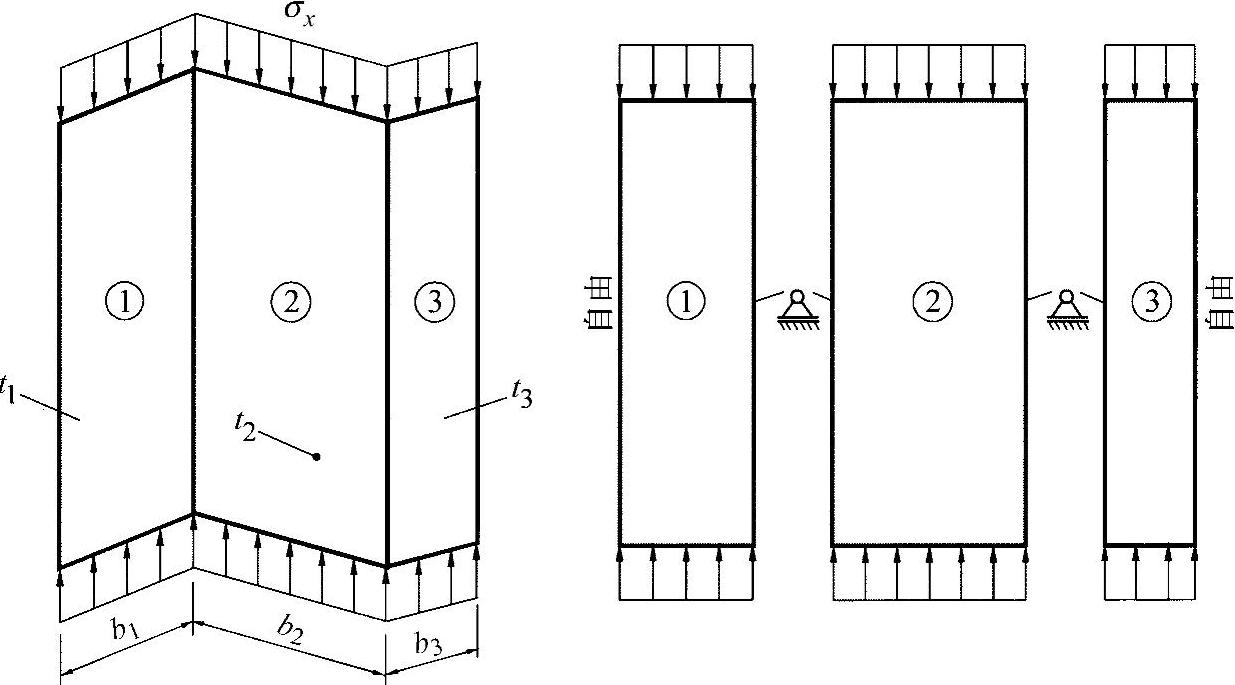
图19-13 Z形展开型材

中间的板条两边固定在刚性棱上，经过计算有：

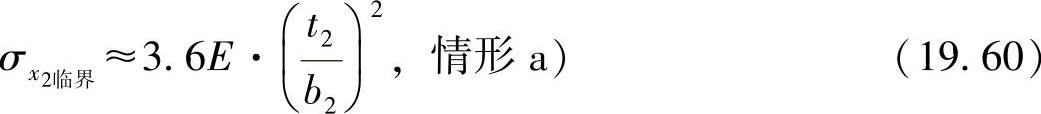
对于基本载荷情形的叠加，上面所描述的简单方法考虑到了型材的力学性能，可提供足够准确的计算结果。