为了阻止板场的凸起,实际中通常有目的地采用下弦杆来进行加固。为说明这一点,这里选择一个、两个或者三个弦杆,它们都设置在力作用的方向上。
加固(在边缘或者在中间)通常根据盘的大小来确定。对于这类加固的有效性来说,首先需要知道的是,一个弦杆必须具有什么样的刚度,以能达到有效的支承效果。
因为这一问题数学上求解比较困难,所以选择一个带有中间弦杆的盘进行示范性的研究。出于简化的原因,这里做出如下假设:
●盘与加固件采用同样的材料;
●加固件与盘的重心轴基本落在盘的中心平面上;
●弦杆的扭转刚度应当可以忽略。
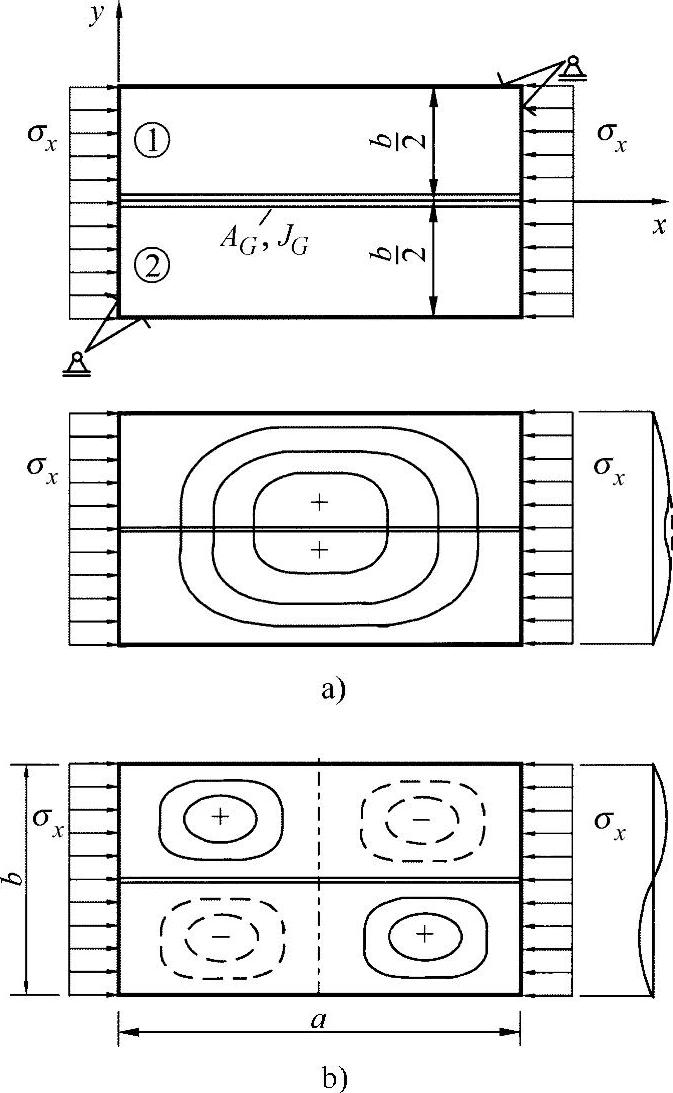
图19-7 加固盘[KOL 58]
a)可能的对称凸起形状 b)反对称凸起形状
图19-7示范性地显示了这样的一个情形。
根据下弦杆的刚度大小,可能会出现两种情况:
●盘与弦杆一起对称性地凸起,即弦杆刚度太小了;
●盘反对称凸起。这里,弦杆总的来说保持平直,即弦杆刚度太大了。
对于反对称凸起的情形,可立即确定出临界凸起应力(19.3节中情形2),该应力对应于一半宽的盘。据此,由方程式(19.17)可得(n=1,α=2α):
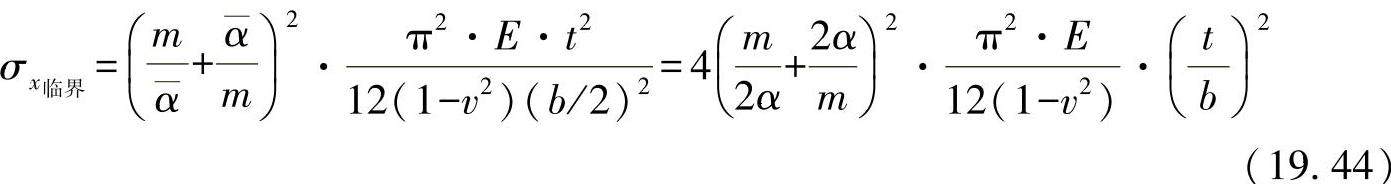
最小波纹数对应于m=2α。如果杆的抗弯刚度足够,这种情形是非常有可能发生的。这样的情形下,即使进一步提高刚度,临界凸起应力也不能再提高。
在对称凸起的情形下,弦杆只呈现很小的抗弯刚度。凸起形状可由下式确定:

现有的边界条件为:一端是铰支,另一端为在弹性基体上的底板(板与弦杆的弯曲相同)。这一问题最终引出特征值方程:
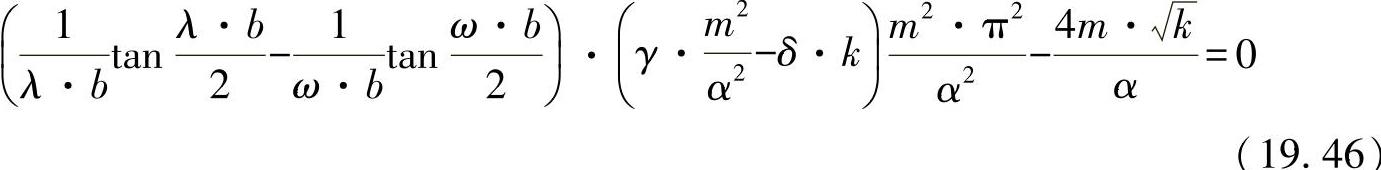
在该方程中引入了如下的简化式:(https://www.xing528.com)
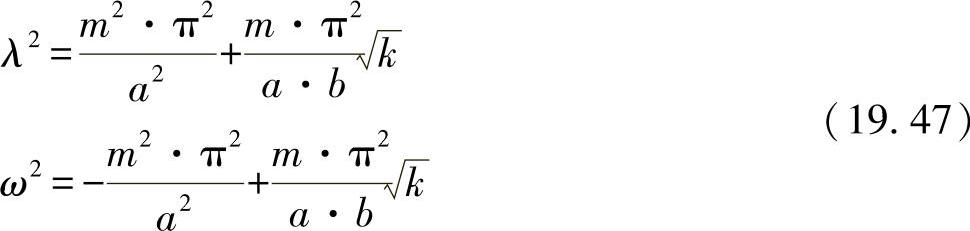
以及系数:

在方程式(19.46)中还有四个未知量,只能通过试验求解。一般来说,可按照后面介绍的方法进行求解。这里,δ值是预先设定的,k可作为刚度γ的变化给出,示例如图19-8所示。
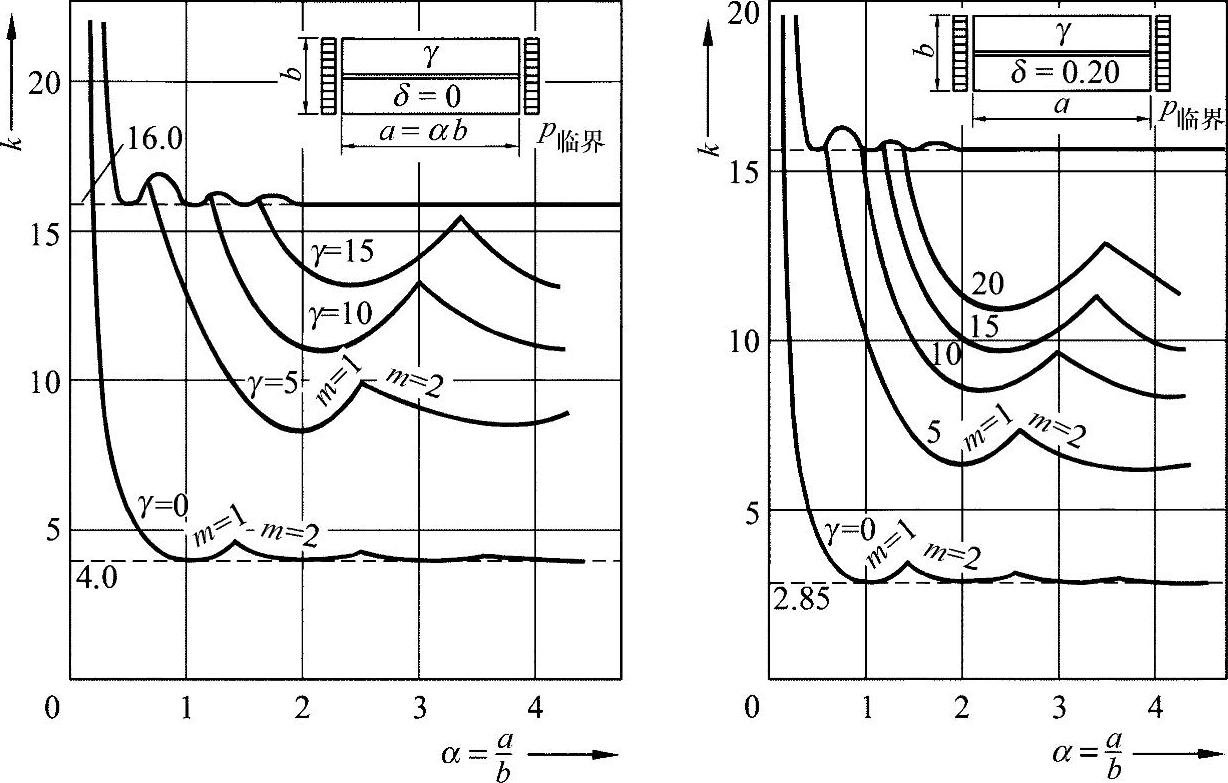
图19-8加固盘的凸起值[KOL 58]
用于阻止凸起的弦杆的最小刚度是反对称的极限情况。如果现在由方程式(19.44)分解凸起值:
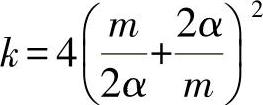
并代入方程式(19.47),则由方程式(19.46)的解即可确定系数γ,由此可得出弦杆尺寸。
按上面的计算,并考虑到:
●对于α>2,凸起值不发生根本变化;
●因为基于b/2,有k极限≈16。
则可得出下面的简化方程:
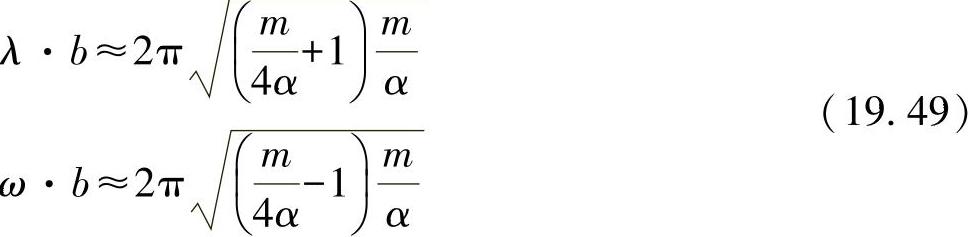
与最小刚度:
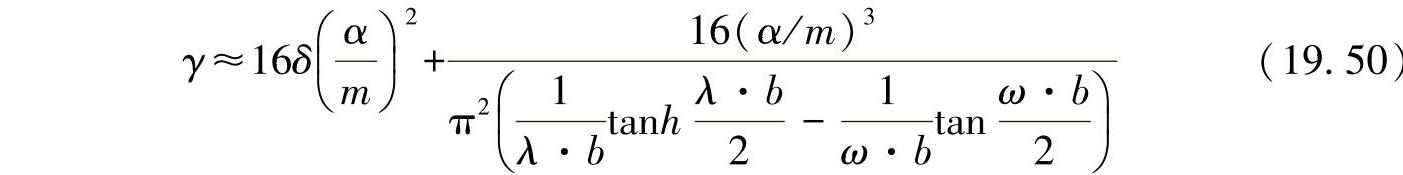
对于确定的几何比例(δ、α、λ、ω),根据预先给出的波纹数m,可计算出弦杆的最小要求抗弯刚度。
采用这种解法可得出相反的吊挂曲线(图19-9),曲线取决于结构的几何形状,并描述了弦杆的最小刚度。
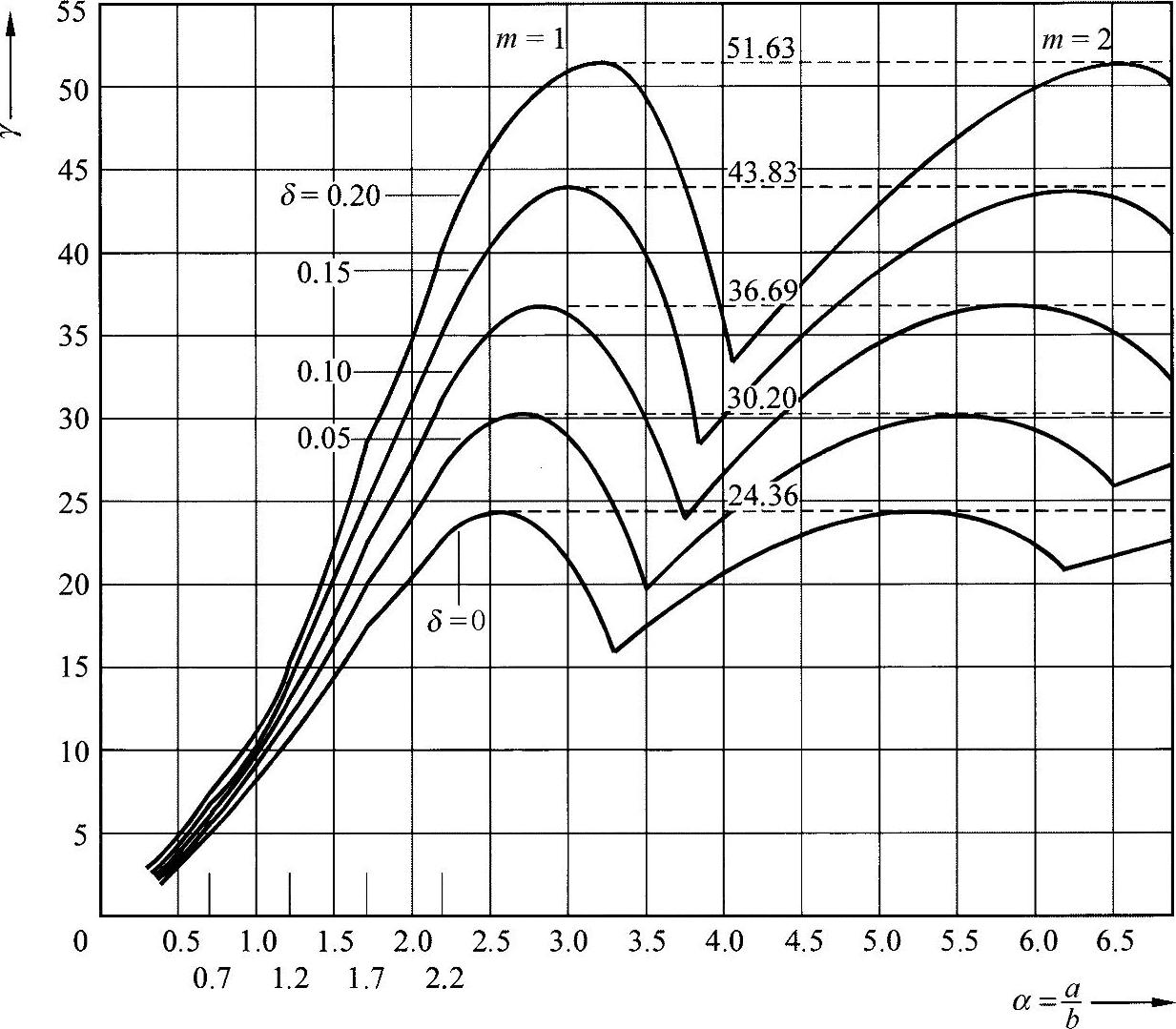
图19-9 阻碍凸起的弦杆的最小刚度变化过程[KOL 58]
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




