管壁凸起，轻量化设计，计算基础与构件结构

另外一个重要的凸起问题是管的不稳定[SZA 84]，如冲击箱体或者风力发电塔。图19-6所示的就是这样的一个凸起情形。从理论上讲，这是一个承受轴向压力的圆缸体外壳。

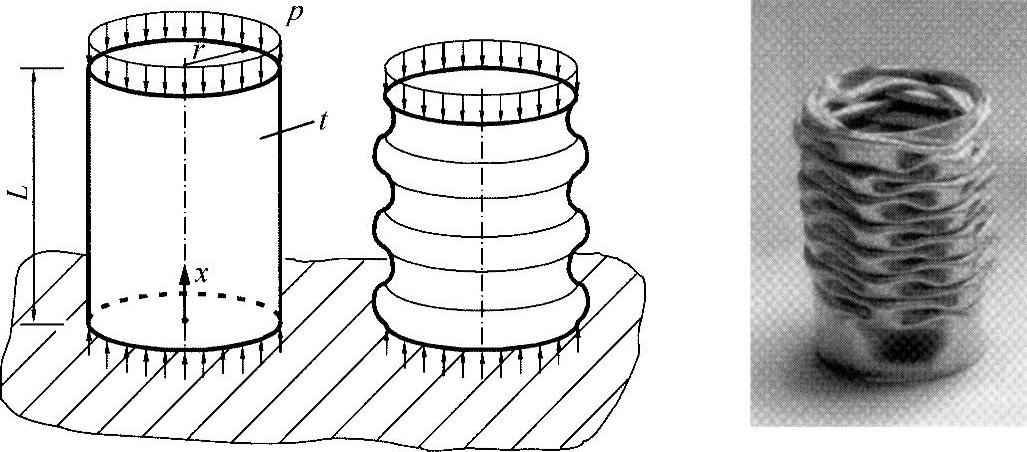
图19-6 缸体管壳的旋转对称凸起

在分析这类问题时，可以首先考虑，将其假设为一个在终端为铰支的杆的压弯（欧拉情形2），则有：

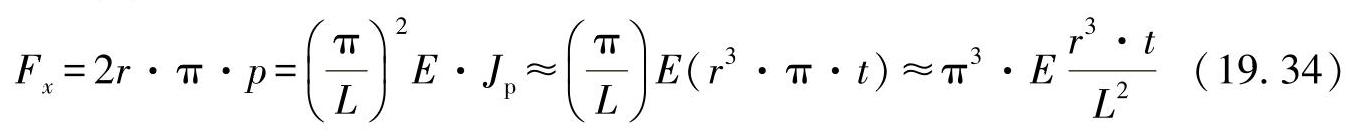
其临界压力为

经验表明，该解法只能近似用于长的、薄壁的管（L>>r）。当长度L和直径2r大小相差不多的时候，比例关系就完全不同了。在载荷作用下，壳壁会产生均匀波纹的皱褶，可将其视为管凸起或者皱褶凸起。这种行为可由圆缸体外壳的弯曲理论推导出。不需推导，即可计算均质微分方程为

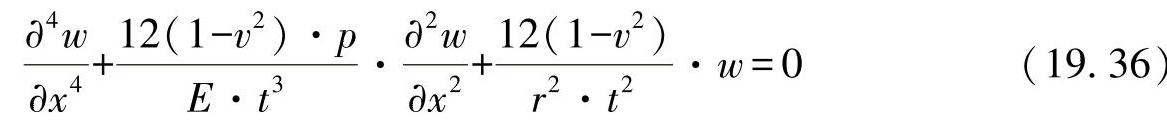
缩写后有：

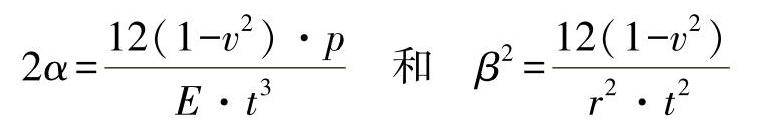
微分方程也可以表示为

w″″（x）+2α·w″（x）+β²·w（x）=0

这一方程形式可满足所有的边界条件，也包括：

w（0）=0，w″（0）=0

w（L）=0，w″（L）=0(www.xing528.com)

其中，

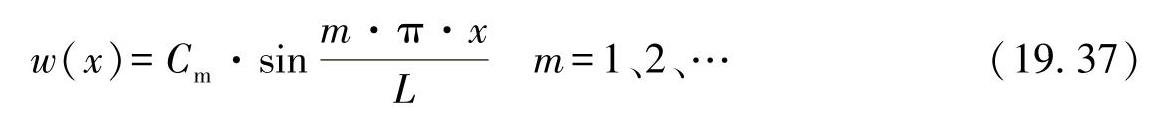
得出相应的导数并将其代入方程式（19.36），可以得出：

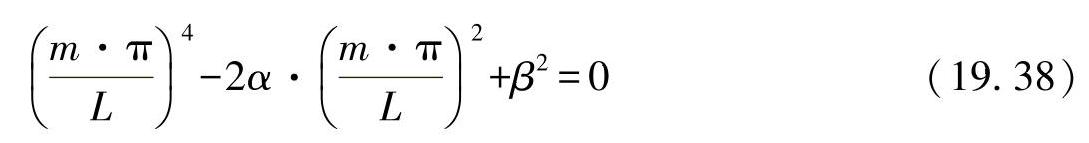
现在将常数2α代回，则上述方程可按照临界轴向压力求解为

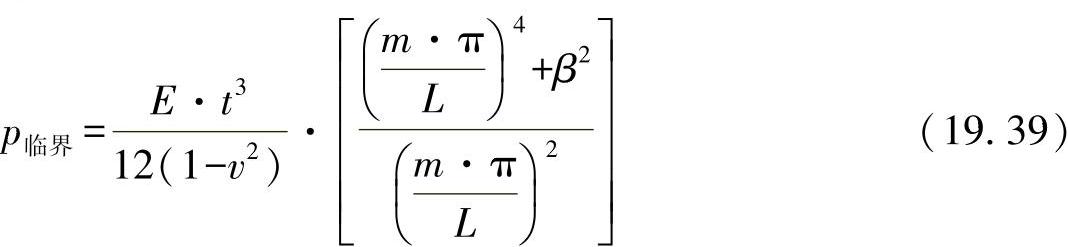
最小值p_临界可由半波长m的最小数字得出，为此，对方程式（19.39）求导：

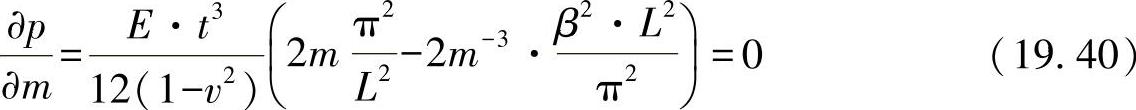
对m由括号表达式可以得出：

m如上所约定的正好为全数字的情况肯定是偶然情形。如果不是这样，那么必须从数学上对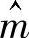进行圆整，所以有：

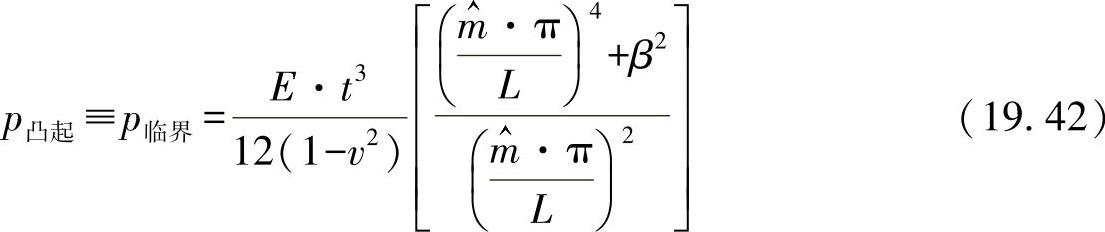
上述方程当然只对应于纯弹性行为与缓慢的加载过程。比较方程式（19.35）与方程式（19.39）可以看出：

如今，管凸起经常应用的一种情形是冲击箱体。在轿车以最大车速15km/h发生碰撞且没有发生结构性损坏的时候，可以通过冲击箱体给予补偿。为此，优先采用的几何形状为圆管或者矩形管。